维数灾难与降维

References：

• 怎样理解 Curse of Dimensionality（维数灾难）?
• 六种常见数据降维方法简介及代码实现
• 机器学习——特征工程之数据降维
• 机器学习-降维

【维数灾难】

维数灾难（Curse of Dimensionality）最初是由 Richard E Bellman 研究动态规划时提出的，是指当维度升高时，会遇到低维场景下察觉不到的困难，对于机器学习来说，维度升高，带来的一个明显的灾难是样本稀疏

基于统计的机器学习本质上都是对数据分布的估计和拟合，为达到这一目的，首先要求的是训练数据的密度达到一定程度，而要想数据密度达到一定程度，所需数据样本的个数将随着维度的增加而急剧增长

具体来说，在样本量一定的情况下，维度越高，样本在空间中的分布越呈现稀疏性，这种稀疏性会带来两个不好的影响：

1）模型参数难以估计，容易出现过拟合

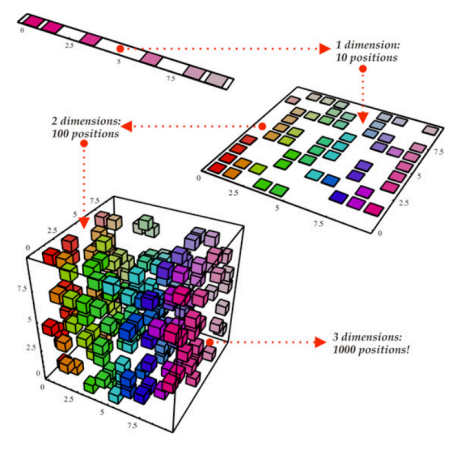
考虑均匀分布下不同维度空间的单位球

• 一维空间：单位球可视为一条 $[0,1]$ 的直线，需要 $N$ 个点才能完全覆盖，两点的平均距离为 $\frac{1}{N}$
• 二维空间：单位球可视为一个 $[0,1]\times[0,1]$ 的正方形，若只有 $N$ 个点，那么两点间的平均距离为 $\sqrt{\frac{1}{n}}$，也就是说如果想维持两点的平均距离为 $\frac{1}{N}$，那么需要 $N^2$ 个点
• 三维空间：单位球可视为一个 $[0,1]\times[0,1]\times[0,1]$ 的正方体，若只有 $N$ 个点，那么两点间的平均距离为 $\sqrt[3]{\frac{1}{n}}$，也就是说如果想维持两点的平均距离为 $\frac{1}{N}$，那么需要 $N^3$ 个点

以此类推，对于 $p$ 维空间，$N$ 个点两两之间的平均距离为：

$$N^{-\frac{1}{p}}$$

或者说，需要 $N^p$ 个点来维持 $\frac{1}{N}$ 的平均距离

那么随着维度的增长，理论上需要指数增长的样本数量覆盖到整个样本空间时，才能保证模型能有效的估计参数，对于具有非线性决策边界的分类器（KNN、决策树、神经网络）来说，如果样本的数量不足，往往会出现过拟合

2）距离失效

对于 $p$ 维空间，假设有 $N$ 个点在单位球内随机分布，那么这 $N$ 个点距离单位球中心距离的中间值计算公式为：

$$\text{dis}(p,N) = (1-\frac{1}{2}^{\frac{1}{N}})^{\frac{1}{p}}$$

当 $p\rightarrow \infty$ 时，$\text{dis}(p,N)\rightarrow 1$，也就是说，随着 $p$ 的增大，这些点会越来越远离单位球的中心，向外缘分散

简单来说，样本分布位于特征空间中心附近的概率，随着维度的增加越来越低，而处在边缘的概率，则越来越高

而对于大小确定的数据集，在特征维度 $p\rightarrow\infty$ 时，数据间的最大距离 $\text{dist}_{\max}$，小于数据间的最小距离 $\text{dist}_{\min}$ 的 $(1+\epsilon)$ 倍的概率将趋近于 $1$，即：

$$\lim_{p\rightarrow \infty} P[\text{dist}_{\max}\leq (1+\epsilon)\text{dist}_{\min}] = 1$$

也就是说，距离这个概念，随着维度的增长，开始在高维空间中失去其测量的有效性

那么对于那些基于距离的模型（KNN、KMeans 等），将会因为维度灾难而有着非常糟糕的性能

【降维】

低维嵌入

缓解维数灾难的一个重要途径就是降维（Dimension Reduction），即通过某种数学变换，将原始高维特征空间转换为一个低维的子空间，在这个子空间中，样本密度大幅提高，距离计算也变得更为容易

降维的核心依据是低维嵌入（Low-dimensional Embedding），即虽然观测或者收集到的数据样本虽然是高维的，但与学习任务密切相关的也许仅是某个低维分布

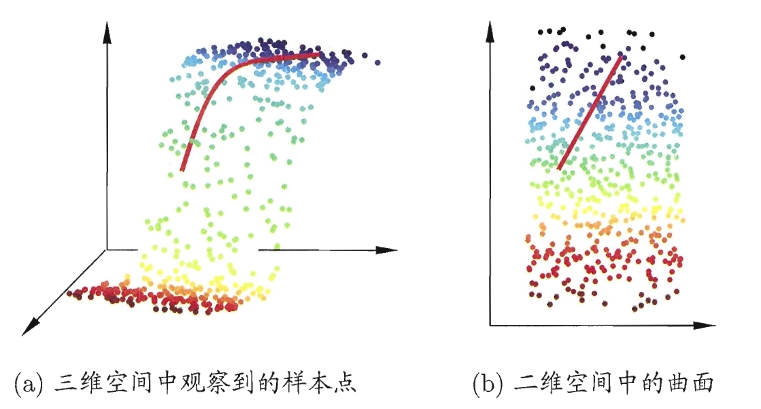
线性降维

一般来说，想要获得低维子空间，最简单的方式是对原始高维空间进行线性变换

对于给定容量为 $n$ 的样本集 $X=\{\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n\} \in \mathbb{R}^{m\times n}$，第 $i$ 个样本的输入 $\mathbf{x}_i$ 具有 $m$ 个特征值，即：$\mathbf{x}_i = (x_i^{(1)},x_i^{(2)},\cdots,x_i^{(m)})\in \mathbb{R}^{m}$

经过线性变换后，得到 $m’\leq m$ 维空间中的样本：

$$Z=W^T X$$

其中，$W\in \mathbb{R}^{m\times m’}$ 是变换矩阵，$Z\in \mathbb{R}^{m’\times m}$ 是样本在低维空间中的表达

变换矩阵 $W$ 可视为 $m’$ 个 $m$ 维向量，$\mathbf{z}_i = W^T \mathbf{x}_i$ 是第 $i$ 个样本 $\mathbf{x}_i$ 与这 $m’$ 个基向量分别进行内积而得到的 $m’$ 维向量，即 $\mathbf{z}_i$ 是原特征向量 $\mathbf{x}_i$ 在新坐标系 $\{\mathbf{w}_1,\mathbf{w}_2,\cdots,\mathbf{w}_{m’}\}$ 中的坐标向量

若 $\mathbf{w}_i$ 与 $\mathbf{w}_j$ 正交（$i\neq j$），则新坐标系是一个正交坐标系，此时 $W$ 为正交变换，显然新的低维空间中的特征是原高维空间中特征的线性组合

这种基于线性变换来进行的降维方法被称为线性降维（Linear Dimensionality Reduction）方法，不同的线性降维方法是对低维子空间的性质有不同的要求，相当于对变换矩阵 $W$ 施加了不同的约束

常见的线性降维方法有：

• 多尺度变换（Multiple Dimensional Scaling，MDS）：又称多维缩放，要求样本在低维空间中的距离与高维空间中的距离尽量保持一致
• 主成分分析（Principal Component Analysis，PCA）：要求低维子空间对样本具有最大可分性
• 线性判别分析（Linear Discriminant Analysis，LDA）：本质是监督学习中的多分类算法，但将样本投影到低维空间的过程可视为降维

非线性降维

在现实数据中，很多情况数据是无法通过线性的方法进行降维表示的，此时就需要使用非线性降维

• 奇异值分解（Singular Value Decomposition，SVD）：矩阵论中一种重要的矩阵分解方法，该方法在机器学习中多用于降维
• 核化线性降维（Kernelized Linear Dimensionality Reduction）：利用核函数对线性降维方法进行核化
  • 核主成分分析（Kernelized Principal Component Analysis，KPCA）：利用核函数对主成分分析进行核化
  • 核线性判别分析（Kernelized Linear Discriminant Analysis，KLDA）：利用核函数对线性判别分析进行核化
• 流形学习（Manifold Learning）：借鉴拓扑流形概念的降维方法，常用于可视化，很少用来生成两个以上的维度进行降维
  • 等距特征映射（Isometric Mapping，ISOMAP）：通过建立邻接图来保留全局结构对数据进行降维
  • 局部线性嵌入（Locally Linear Embedding，LLE）：从局部结构出发对数据进行降维