主成分分析 PCA

【概述】

统计分析中，数据的变量之间可能存在相关性，以致增加了分析的难度。那么，考虑用少数不相关的变量来代替相关的变量，以表示数据，并且要求能够保留数据中的大部分信息

主成分分析（Principal Component Analysis，PCA）的基本思想，具体来说，首先对给定数据进行规范化，使得数据每一变量的均值为 $0$，方差为 $1$，之后对数据进行正交变换，将原来由线性相关变量表示的数据，变换成由若干个线性无关的新变量表示的数据，其中，新变量是正交变换中变量的方差和最大的，方差表示了新变量上信息的大小，这些新变量依次被称为第一主成分、第二主成分等

通过上述的主成分分析，可以用主成分近似地来表示原始数据，这个过程可理解为发现数据的基本结构，将数据用少数主成分来表示，即对数据降维

【直观解释】

数据集合中的样本由实数空间中的点表示，实数空间中的一个坐标轴表示一个变量，规范化处理后得到的数据分布在原点附近

对原坐标系中的数据进行主成分分析等价于进行坐标系旋转变换，将数据投影到新坐标系的坐标轴上，新坐标系的第一坐标轴、第二坐标轴等分别表示第一主成分、第二主成分等，数据在每一个轴上的坐标值的平方表示相应变量的方差，同时，这个坐标系是在所有可能的新的坐标系中，坐标轴上的方差和最大的

如下图所示，样本点存在于二维空间中，由两个变量 $x_1$​ 和 $x_2$​ 表示，进行规范化处理后，这些数据分布在以原点为中心的左下至右上倾斜的椭圆之内，显然变量 $x_1$ 和 $x_2$ 是线性相关的，当知道其中一个变量的取值时，对另一个变量的预测不是完全随机的

主成分分析对数据进行正交变换，具体来说，是对原坐标系进行旋转变换，选择方差最大的方向（第一主成分）作为新坐标系的第一坐标轴，即 $y_1$ 轴，在这里意味着选择椭圆的长轴作为新坐标系的第一坐标轴，之后选择与第一坐标轴正交，且方差次之的方向（第二主成分）作为新坐标系的第二坐标轴，即 $y_2$​​ 轴，在这里意味着选择椭圆的短轴作为新坐标系的第二坐标轴

在新坐标系里，数据中的变量 $y_1$ 和 $y_2$ 是线性无关的，当知道其中一个变量 $y_1$ 的取值时，对另一个变量 $y_2$​ 的预测是完全随机的

如果主成分分析只取第一主成分，即新坐标系的 $y_1$ 轴，那么等价于将数据投影在椭圆长轴上，用这个主轴表示数据，将二维空间的数据压缩到一维空间中

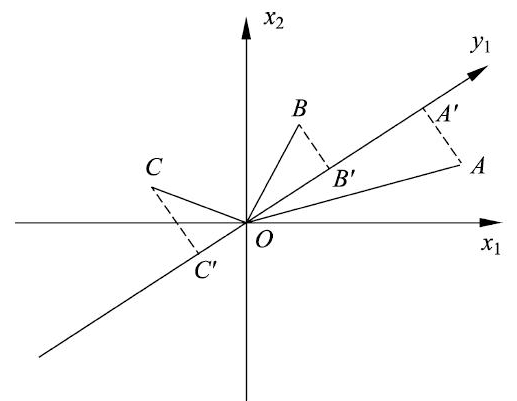
对于方差最大来说，假设三个样本点 $A,B,C$ 分布在由 $x_1$ 轴和 $x_2$ 轴组成的坐标系中，对坐标系进行旋转变换，得到新的坐标轴 $y_1$，样本点 $A,B,C$ 在 $y_1$ 轴上投影的为 $A’,B’,C’$，坐标的平方和 $OA’^2＋OB’^2＋OC’^2$ 表示样本在轴 $y_1$ 上的方差和

主成分分析旨在选取正交变换中方差最大的变量作为第一主成分，也就是旋转变换中坐标值的平方和最大的轴

由于旋转变换中样本点到原点的距离的平方和 $OA^2＋OB^2＋OC^2$ 保持不变，根据勾股定理，坐标值的平方和 $OA’^2＋OB’^2＋OC’^2$ 最大等价于样本点到 $y_1$ 轴的距离的平方和 $AA’^2＋BB’^2＋CC’^2$ 最小

所以，主成分分析在旋转变换中选取离样本点的距离平方和最小的轴，作为第一主成分，而第二主成分等的选取，在保证与已选坐标轴正交的条件下，类似地进行

【总体主成分分析】

定义

在数据总体上进行的主成分分析被称为总体主成分分析（Population Principal Component Analysis，Population PCA），其是在有限样本上进行的样本主成分分析（Sample Principal Component Analysis，Sample PCA）的基础

假设 $\mathbf{x} = (x_1,x_2,\cdots,x_m)^T$ 是 $m$​ 维随机变量，其均值向量是

$$\boldsymbol{\mu}=E(\mathbf{x})=(\mu_1,\mu_2,\cdots,\mu_m)^T$$

其协方差矩阵是

$$\Sigma=\text{cov}(\mathbf{x},\mathbf{x}) = E[(\mathbf{x}-\boldsymbol{\mu})(\mathbf{x}-\boldsymbol{\mu})^T]$$

考虑由 $m$ 维随机变量 $\mathbf{x}$ 到 $m$ 维随机变量 $\mathbf{w}=(w_1,w_2,\cdots,w_m)^T$ 的线性变换

$$w_i = \alpha_i^T \mathbf{x} = \alpha_{1i}x_1 + \alpha_{2i}x_2 + \cdots + \alpha_{mi}x_m$$

其中，$\alpha_i^T=(\alpha_{1i},\alpha_{2i},\cdots,\alpha_{mi}),i=1,2,\cdots,m$

根据随机变量的性质，有：

$$\begin{gather*} E(w_i) = \alpha_i^T \boldsymbol{\mu}, & i=1,2,\cdots,m \\ \text{var}(w_i) = \alpha_i^T \Sigma\alpha_i, & i=1,2,\cdots,m \\ \text{cov}(w_i,w_j) = \alpha_i^T \Sigma a_j, & i,j=1,2,\cdots,m \end{gather*}$$

若上述的线性变换满足：

1. 系数向量 $\alpha_i^T$ 是单位向量，即 $\alpha_{i}^{T} \alpha_i = 1,i=1,2,\cdots,m$
2. 变量 $w_i$ 与 $w_j$ 互不相关，即 $\text{cov}(w_i,w_j)=0,i\neq j$
3. 变量 $w_1$ 是 $\mathbf{x}$ 的所有线性变换中方差最大的，$w_i$ 是与 $w_1,w_2,\cdots,w_{i-1},i=2,\cdots,m$ 都不相关的 $\mathbf{x}$ 的所有线性变换中方差最大的

此时，分别称 $w_1,w_2,\cdots,w_m$ 为 $\mathbf{x}$ 的第一主成分、第二主成分、$\cdots$、第 $m$ 主成分

---

可以发现，上述定义的条件 1 表明线性变换是正交变换，$\alpha_1,\alpha_2,\cdots,\alpha_m$ 是一组标准正交基，即

$$\alpha_i^T \alpha_j = \left\{\begin{array}{cc} 1, & i = j \\ 0, & i \neq j \end{array}\right.$$

同时，条件 2、3 给出了一个求主成分的方法：

Step 1：在 $\mathbf{x}$ 的所有线性变换中，在 $\alpha_1^T\alpha_1=1$ 条件下，求方差最大的，得到 $\mathbf{x}$ 的第一主成分 $w_1$

Step 2：在与 $\alpha_1^T\mathbf{x}$ 不相关的 $\mathbf{x}$ 的所有线性变换

$$\alpha_2^T \mathbf{x} = \sum_{i=1}^m \alpha_{i2}x_i$$

中，在 $\alpha_2^T\alpha_2=1$ 条件下，求方差最大的，得到 $\mathbf{x}$ 的第二主成分 $w_2$

Step k：在与 $\alpha_1^T\mathbf{x},\alpha_2^T\mathbf{x},\cdots,\alpha_{k-1}^T\mathbf{x}$ 不相关的 $\mathbf{x}$ 的所有线性变换

$$\alpha_k^T \mathbf{x} = \sum_{i=1}^m \alpha_{ik}x_i$$

中，在 $\alpha_k^T\alpha_k=1$ 条件下，求方差最大的，得到 $\mathbf{x}$ 的第 $k$ 主成分 $w_k$

以此类推，直到得到 $\mathbf{x}$ 的第 $m$ 主成分 $w_m$

主成分的个数

理论依据

主成分分析的主要目的是降维，所以一般选择 $k\ll m$ 个主成分来代替原有的 $m$ 个线性相关变量，使得问题简化，并能保留原有变量的大部分信息（方差）

对于任意正整数 $1\leq q\leq m$，考虑正交线性变换

$$\mathbf{w}=B^T \mathbf{x}$$

其中，$\mathbf{w}$ 是 $q$ 维向量，$B^T$ 是 $q\times m$ 维矩阵，令 $\mathbf{w}$ 的协方差矩阵为：

$$\Sigma_w = b^T \Sigma B$$

则 $\Sigma_w$ 的迹 $\text{tr}(\Sigma_w)$ 在 $B=A_q$ 时取得最大值，其中矩阵 $A_q$ 由正交矩阵 $A$ 的前 $q$ 列组成

上述定理表明，当 $\mathbf{x}$ 的线性变换 $\mathbf{w}$ 在 $B=A_q$ 时，其协方差矩阵 $\Sigma_w$ 的迹 $\text{tr}(\Sigma_w)$ 取得最大值，即当取 $A$ 的前 $q$ 列（取 $\mathbf{x}$ 的前 $q$ 个主成分）时，能够最大限度地保留原有变量方差的信息

同时，当 $\text{tr}(\Sigma_w)$ 在 $B=A_p$ 时，取得最小值，其中 $A_p$ 由 $A$ 的后 $p$ 列组成，即舍弃 $A$ 的后 $p$ 列（舍弃 $\mathbf{x}$ 的后 $p$​ 个主成分）时，原有变量的方差的信息损失最少

方差贡献率

上述定理，可以作为选择 $k$ 个主成分的理论依据，具体选择 $k$ 的方法，通常利用方差贡献率

第 $k$ 个主成分 $w_k$ 的方差贡献率定义为 $w_k$ 的方差与所有方差和的比，记作：

$$\eta_k = \frac{\lambda_k}{\sum\limits_{i=1}^m \lambda_i}$$

$k$ 个主成分 $w_1,w_2,\cdots,w_k$ 的累计方差贡献率定义为 $k$ 个方差和与所有方差和的比值，即：

$$\sum_{i=1}^k \eta_i = \frac{\sum\limits_{i=1}^k \lambda_i}{\sum\limits_{i=1}^m \lambda_i}$$

通常取 $k$ 使得累计方差贡献率达到规定的百分比以上，通常取 $70\%\sim80\%$ 左右

主成分对原有变量的贡献率

累计方差贡献率反映了主成分保留信息的比例，但无法反映对某个原有变量 $x_i$ 保留信息的比例

此时通常利用 $k$ 个主成分 $w_1,w_2,\cdots,w_k$ 对原有变量 $x_i$ 的贡献率，其被定义为 $x_i$ 与 $(w_1,w_2,\cdots,w_k)$ 的相关系数的平方，记作：

$$\begin{align*} \nu_i &= \rho^2(x_i,(w_1,w_2,\cdots,w_k)) \\ &= \sum_{j=1}^k \rho^2(x_i,w_j) \\ &= \sum_{j=1}^k \frac{\lambda_j \alpha_{ij}^2}{\sigma_{ij}} \end{align*}$$

规范化变量

在实际应用中，不同变量可能有不同的量纲，直接求主成分有时会产生不合理的结果，为消除这种影响，通常会对各个随机变量进行规范化处理，使其均值为 $0$，方差为 $1$

设 $\mathbf{x} = (x_1,x_2,\cdots,x_m)^T$ 为 $m$ 维随机变量，令

$$x_i^* = \frac{x_i-E(x_i)}{\text{var}(x_i)},\quad i=1,2,\cdots,m$$

其中，$E(x_i),\text{var}(x_i)$ 分别是随机变量 $x_i$ 的均值和方差，此时 $x_i^{*}$ 就是 $x_i$ 的规范化随机变量

显然，规范化随机变量的协方差矩阵就是相关矩阵 $R$​，主成分分析通常在规范化随机变量的协方差矩阵即相关矩阵上进行

【样本主成分分析】

定义

在实际应用中，需要在观测数据上进行主成分分析，即样本主成分分析（Sample Principal Component Analysis，Sample PCA），一般常说的主成分分析 PCA，就是指样本主成分分析

对 $m$ 维随机变量 $\mathbf{x}=(x_1,x_2,\cdots,x_m)^T$ 进行 $n$ 次独立观测，$\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n$ 表示观测样本，其中 $\mathbf{x}_j=(x_{1j},x_{2j},\cdots,x_{mj})^T,j=1,2,\cdots,n$ 表示第 $j$ 个观测样本

将观测数据用样本矩阵 $X$ 来表示，记作：

$$X=[\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n] = \begin{bmatrix} x_{11} & x_{12} & \cdots & x_{1n} \\ x_{21} & x_{22} & \cdots & x_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ x_{m1} & x_{m2} & \cdots & x_{mn} \\ \end{bmatrix}$$

定义 $m$ 维向量 $\mathbf{x}=(x_1,x_2,\cdots,x_m)^T$ 到 $m$ 维向量 $\mathbf{w}=(w_1,w_2,\cdots,w_m)^T$ 的线性变换

$$\begin{gather*} \mathbf{w} = A^T\mathbf{x} \\ A=[\mathbf{a}_1,\mathbf{a}_2,\cdots,\mathbf{a}_m] = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1m} \\ a_{21} & a_{22} & \cdots & a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mm} \\ \end{bmatrix} \end{gather*}$$

那么，样本矩阵 $X$ 的第一主成分 $\mathbf{w}_1=\mathbf{a}_1^T\mathbf{x}$ 是在 $\mathbf{a}_1^T\mathbf{a}_1=1$ 的条件下，使得 $\mathbf{a}_1^T\mathbf{x}_{j},j=1,2,\cdots,n$ 的样本方差 $\mathbf{a}_1^TS_{\mathbf{a}_1}$ 最大的 $\mathbf{x}$ 的线性变换，样本的第 $i$ 主成分 $\mathbf{w}_i=\mathbf{a}_i^T\mathbf{x}$ 是在 $\mathbf{a}_i^T\mathbf{a}_i=1$，和 $\mathbf{a}_i^T\mathbf{x}_j$ 与 $\mathbf{a}_k^T\mathbf{x}_j(k<i,j=1,2,\cdots,n)$ 的样本协方差 $\mathbf{a}_k^TS_{\mathbf{a}_i}=0$ 的条件下，使得 $\mathbf{a}_i^T\mathbf{x}_{j},j=1,2,\cdots,n$ 的样本方差 $\mathbf{a}_i^TS_{\mathbf{a}_i}$ 最大的 $\mathbf{x}$ 的线性变换

规范化变量

使用样本主成分分析时，一般假设样本数据是规范化的，即对样本矩阵进行如下变换：

$$x_{ij}^{*} = \frac{x_{ij}-\overline{x}_i}{\sqrt{s_{ii}}},\quad i=1,2,\cdots,m;j=1,2,\cdots,n$$

其中

$$\begin{gather*} \overline{x}_i = \frac{1}{n} \sum_{j=1}^n x_{ij}, & i=1,2,\cdots,m \\ s_{ii} = \frac{1}{n-1}\sum_{j=1}^n(x_{ij}-\overline{x}_i), & i=1,2,\cdots,m \end{gather*}$$

相关矩阵的特征值分解算法

给定样本矩阵 $X$，利用数据的样本协方差或者样本相关矩阵的特征值分解进行主成分分析，具体步骤如下：

Step1：将观测数据按照 $x_{ij}^{*} = \frac{x_{ij}-\overline{x}_i}{\sqrt{s_{ii}}}$ 进行规范化处理，得到规范化数据矩阵，为便于表达，仍用 $X$ 表示

Step2：利用规范化数据矩阵 $X$，计算样本相关矩阵 $R$

$$\begin{gather*} R=[r_{ij}]_{m\times m} = \frac{1}{n-1} XX^T \\ r_{ij} = \frac{1}{n-1} \sum_{l=1}^n x_{il}x_{lj},\quad i,j=1,2,\cdots,m \end{gather*}$$

Step3：求样本相关矩阵 $R$ 的 $k$ 个特征值和对应的 $k$ 个单位特征向量

求解 $R$ 的特征方程

$$|R-\lambda I| = 0$$

得到 $R$ 的 $m$ 个特征值

$$\lambda_1\geq \lambda_2 \geq \cdots \geq \lambda_m$$

求方差贡献率 $\sum\limits_{i=1}^k \eta_i$ 达到预定值的主成分个数 $k$，并求前 $k$ 个特征值对应的单位特征向量

$$\mathbf{a}_i = (a_{1i},a_{2i},\cdots,a_{mi})^T,\quad i=1,2,\cdots,k$$

Step4：以 $k$ 个单位特征向量为系数，进行线性变换，求出 $k$ 个样本主成分

$$\mathbf{w}_i = \mathbf{a}_i^T\mathbf{x},\quad i=1,2,\cdots,k$$

Step5：计算 $k$ 个主成分 $\mathbf{w}_j$ 与原变量 $\mathbf{x}_i$ 的相关系数 $\rho(\mathbf{x}_i,\mathbf{w}_j)$，以及 $k$ 个主成分对原变量 $\mathbf{x}_i$ 的贡献率 $\nu_i$

Step6：将规范化样本数据代入 $k$ 个主成分值，得到投影矩阵

$$W=[\mathbf{w}_1,\mathbf{w}_2,\cdots,\mathbf{w}_k]$$

其中，第 $j$ 个样本 $\mathbf{x}_j=(x_{1j},x_{2j},\cdots,x_{mj})^T$ 的第 $i$ 个主成分值是

$$\begin{align*} w_{ij} &= (a_{1i},a_{2i},\cdots,a_{mi})(x_{1j},x_{2j},\cdots,x_{mj})^T \\ &=\sum_{l=1}^m a_{li} x_{lj}\\ & i=1,2,\cdots,m, \quad j=1,2,\cdots,n \end{align*}$$

【sklearn 实现】

以 sklearn 中的鸢尾花数据集为例，将降维到二维空间来可视化

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA

# 特征提取
def deal_data():
    iris = load_iris()  # sklearn的鸢尾花数据集
    # iris分为三类，前50行一类，51-100行一类，101-150行一类
    X = iris.data
    y = iris.target
    return X, y

# 数据标准化
def standard_scaler(X):
    sc = StandardScaler() # 初始化一个sc对象去对数据集作变换
    scaler = sc.fit(X) # 归一化，存有计算出的均值和方差
    X_std = scaler.transform(X) # 利用 scaler 进行标准化
    return X_std

# 模型训练
def train_model(features):
    # 建立PCA模型
    model = PCA(n_components=2, random_state=42)
    # 降维
    result = model.fit_transform(features)
    return result

# 可视化
def visualization(X, y):
    plt.scatter(X[:,0], X[:,1], c=y, s=10)
        
    plt.xlabel('x1')
    plt.ylabel('x2')
    plt.legend(loc='upper left')
    plt.tight_layout()
    plt.show()


if __name__ == "__main__":
    # 数据处理
    X, y = deal_data()

    # 数据标准化
    X_std = standard_scaler(X)

    # 获取降维结果
    result = train_model(X_std)

    # 可视化
    visualization(result, y)