Alex_McAvoy

想要成为渔夫的猎手

线性判别分析 LDA

发表于 分类于 ， ，
本文字数： 8k 阅读时长 ≈ 7 分钟

References：

【概述】

线性判别分析（Linear Discriminant Analysis，LDA）也是一种常用的降维技术，但与 PCA 不同的是，其是一种监督学习的降维技术，当具有 $K$ 类别时，最多降到 $K-1$ 维，此外，其还可用于分类

其基本思想是最大化类间均值，最小化类内方差，即将数据投影在低维度上，并且投影后同种类别数据的投影点尽可能的接近，不同类别数据的投影点的中心点尽可能的远

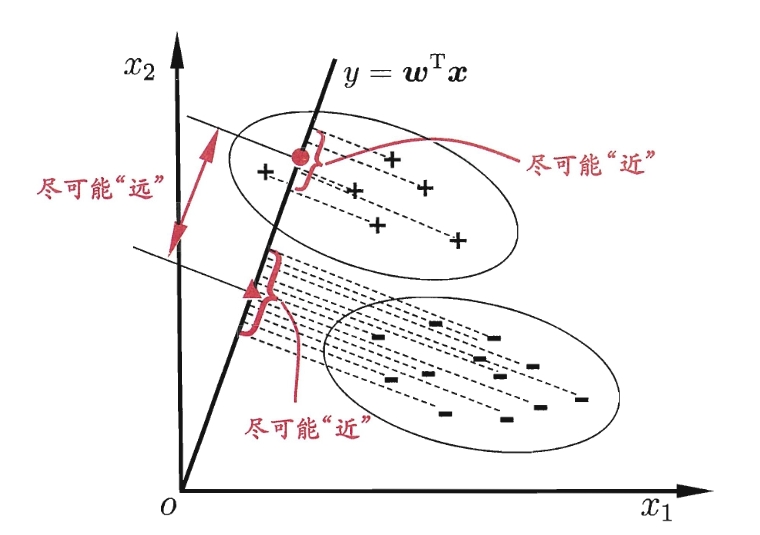
【基本思想】

均值向量

对于给定的样本集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),\cdots,(\mathbf{x}_n,y_n)\}$，第 $i$ 个样本的输入 $\mathbf{x}_i$ 具有 $m$ 个特征值，即：$\mathbf{x}_i = (x_i^{(1)},x_i^{(2)},\cdots,x_i^{(m)})\in \mathbb{R}^{m}$，输出 $y_i\in\{C_1,C_2,\cdots,C_K\}$

由于一共有 $K$ 类，假设每一类的样本个数分别为 $N_1,N_2,\cdots,N_K$，用 $X_k = (\mathbf{x}_1^{k},\mathbf{x}_2^{k},\cdots,\mathbf{x}_{N_k}^{k})$ 来表示第 $k$​ 类中的样本

设 $\tilde{\mathbf{x}}_i^k$ 为第 $k$ 类中第 $i$ 个样本 $\mathbf{x}_{i}^k$ 投影到直线 $\mathbf{w}$ 后的样本，则有：

为便于记录，将 $\tilde{\mathbf{x}}_i^k = \big((\mathbf{x}_{i}^k)^T \mathbf{w}\big)\mathbf{w}$ 简记为 $\tilde{\mathbf{x}}_i^k =(\mathbf{x}^T \mathbf{w})\mathbf{w}$

其中，$\mathbf{w}$ 为单位向量，即 $\mathbf{w}^T\mathbf{w}=1$

假设第 $k$ 类样本的数据集为 $D_k$，投影后的样本的均值向量为

方差

那么，第 $k$ 类样本的方差为 $\frac{S_k}{N_k}$，其中

由于 $\mathbf{x}^T\mathbf{w}$ 与 $\mathbf{m}^T\mathbf{w}$ 为实数，转置后仍为其本身，故有：

因此，对于方差 $\frac{S_k}{N_k}$，有：

类内散度矩阵

那么，各类别的样本方差和为：

其中，$S_w = \sum\limits_{k=1}^K \Big( \frac{\sum\limits_{\mathbf{x}\in D_k}\mathbf{x}\mathbf{x}^T}{N_k} -\mathbf{m}\mathbf{m}^T \Big)$ 被称为类内散度矩阵（Within-class Scatter Matrix）

类间散度矩阵

对于不同类别 $i,j$ 间的中心距离，有：

所有类别之间的距离和为：

其中，$S_b=\sum\limits_{i,j,i\neq j} (\mathbf{m}_i-\mathbf{m}_j)(\mathbf{m}_i-\mathbf{m}_j)^T$ 被称为类间散度矩阵（Between-class Scatter Matrix）

优化目标

在已知条件下，类内散度矩阵 $S_w$ 和类间散度矩阵 $S_b$ 均可求出，LDA 算法的基本思想是最大化类间均值，最小化类内方差，即最大化 $\mathbf{w}^TS_b\mathbf{w}$，最小化 $\mathbf{w}^TS_w\mathbf{w}$

令目标函数为：

可以发现，LDA 想要最大化的目标，即 $S_b$ 与 $S_w$ 的广义瑞利商

注意到，上式的分子和分母都是关于 $\mathbf{w}$ 的二次项，因此上式的解与 $\mathbf{w}$ 的长度无关，只与方向有关

为不失一般性，令 $\mathbf{w}^TS_w\mathbf{w}=1$，则问题转换为：

根据拉格朗日乘子法，设拉格朗日函数为：

求导有：

容易证明 $S_b$ 和 $S_w$ 均为对称矩阵，故有：

易得：

故而只需计算矩阵 $S_w^{-1}S_b$ 的最大的 $d$ 个特征值和对应的 $d$ 个特征向量 $(\mathbf{w}_1,\mathbf{w}_2,\cdots,\mathbf{w}_d)$，即可得到投影矩阵

之后，利用投影矩阵，将 $n$ 个样本的输入 $\mathbf{x}_i$ 转为降维后的样本，即：

【算法流程】

输入：样本集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),\cdots,(\mathbf{x}_n,y_n)\}$，第 $i$ 个样本的输入 $\mathbf{x}_i$ 具有 $m$ 个特征值，即：$\mathbf{x}_i = (x_i^{(1)},x_i^{(2)},\cdots,x_i^{(m)})\in \mathbb{R}^{m}$，输出 $y_i\in\{C_1,C_2,\cdots,C_K\}$；降维到的维度 $d$

输出：降维后的数据集 $D’=\{(\mathbf{z}_1,y_1),(\mathbf{z}_2,y_2),\cdots,(\mathbf{z}_n,y_n)\}$，，第 $i$ 个样本的输入 $\mathbf{z}_i$ 具有 $d$ 个特征值，即：$\mathbf{z}_i = (z_i^{(1)},z_i^{(2)},\cdots,z_i^{(d)})\in \mathbb{R}^{d}$，

算法流程：

Step1：计算类内散度矩阵

Step2：计算类间散度矩阵

Step3：计算矩阵 $S_w^{-1}S_b$

Step4：计算矩阵 $S_w^{-1}S_b$ 的特征向量，按从小到大的顺序选取前 $d$ 个特征值和对应的特征向量 $(\mathbf{w}_1,\mathbf{w}_2,\cdots,\mathbf{w}_d)$​，得到投影矩阵

Step5：对样本集中的每一个样本 $\mathbf{x}_i$，转换为新的样本

Step6：输出样本集

【sklearn 实现】

以 sklearn 中的鸢尾花数据集为例，将降维到二维空间来可视化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis as LDA

# 特征提取
def deal_data():
    iris = load_iris()  # sklearn的鸢尾花数据集
    # iris分为三类，前50行一类，51-100行一类，101-150行一类
    X = iris.data
    y = iris.target
    return X, y

# 数据标准化
def standard_scaler(X):
    sc = StandardScaler() # 初始化一个sc对象去对数据集作变换
    scaler = sc.fit(X) # 归一化，存有计算出的均值和方差
    X_std = scaler.transform(X) # 利用 scaler 进行标准化
    return X_std

# 模型训练
def train_model(features, y):
    # 建立LDA模型
    model = LDA(n_components=2)
    # 降维
    result = model.fit_transform(features, y)
    return result

# 可视化
def visualization(X, y):
    plt.scatter(X[:,0], X[:,1], c=y, s=10)
        
    plt.xlabel('x1')
    plt.ylabel('x2')
    plt.legend(loc='upper left')
    plt.tight_layout()
    plt.show()


if __name__ == "__main__":
    # 数据处理
    X, y = deal_data()

    # 数据标准化
    X_std = standard_scaler(X)

    # 获取降维结果
    result = train_model(X_std, y)

    # 可视化
    visualization(result, y)
感谢您对我的支持，让我继续努力分享有用的技术与知识点！