【奇异值】
设 $A\in C^{m\times n}$,记非负定 Hermite 阵 $A^HA$ 的 $n$ 个特征值为
称
为 $A$ 的奇异值(Singular Value)
若 $\text{rank } A=r$,则 $A^HA$ 具有 $r$ 个正的特征值,通常设
称 $\sigma_1,\sigma_2,\cdots,\sigma_r$ 为 $A$ 的正奇异值
【奇异值分解】
定义
设 $A\in C^{m\times n},\text{rank } A=r>0$,则称 $U\Sigma V^T$ 为 $A$ 的奇异值分解(Singular Value Decomposition,SVD),即:
其中,$U$ 为 $m$ 阶酉矩阵,$V$ 为 $n$ 阶酉矩阵,$\Sigma_r=\text{diag }(\sigma_1,\sigma_2,\cdots,\sigma_r)$,$\sigma_1\geq \sigma_2\geq \cdots \geq \sigma_r>0$ 为 $A$ 的 $r$ 个正奇异值
奇异值分解 $A=U\Sigma V^T$ ,又称完全奇异值分解(Full Singular Value Decomposition),实际常用的是奇异值分解的紧凑形式与截断形式
几何意义
从线性变换的角度来看,$m\times n$ 维的矩阵 $A$ 表示从 $n$ 维空间 $C^n$ 到 $m$ 维空间 $C^{m}$ 的一个线性变换,即:
其中,$x\in C^n$ 是 $n$ 维空间 $C^n$ 的向量,$Ax\in C^m$ 是 $m$ 维空间 $C^{m}$ 的向量
具体来说,对 $A$ 的奇异值分解 $U\Sigma V^T$,$U$ 与 $V$ 都是正交矩阵,所以 $V$ 的列向量 $v_1,v_2,\cdots,v_n$ 构成 $C^n$ 空间的一组标准正交基,表示 $C^n$ 中的正交坐标系的旋转或反射变换,$U$ 的列向量 $u_1,u_2,\cdots,u_n$ 构成 $C^m$ 空间的一组标准正交基,表示 $C^m$ 中的正交坐标系的旋转或反射变换,$\Sigma$ 的对角元素 $\sigma_1,\sigma_2,\cdots,\sigma_n$ 是一组非负实数,表示 $C^n$ 中的原始正交坐标系坐标轴 $\sigma_1,\sigma_2,\cdots,\sigma_n$ 倍的缩放变换
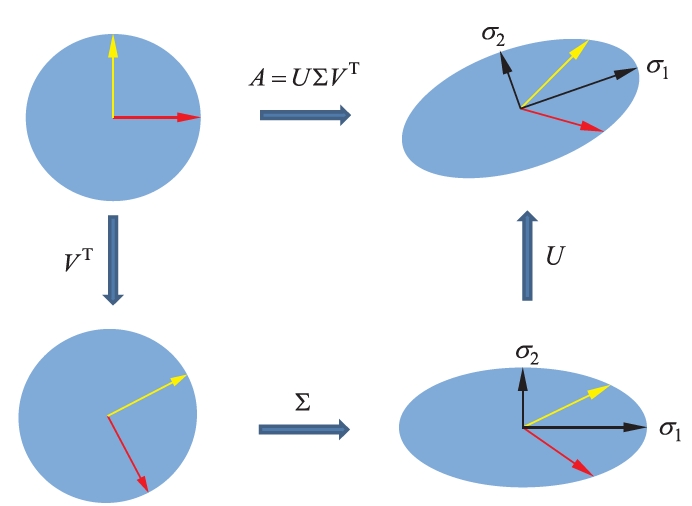
也就是说,对任意一个向量 $x\in C^n$,经过基于 $A=U\Sigma V^T$ 的线性变换,等价于经过坐标系的旋转或反射变换 $V^T$,坐标轴的缩放变换 $\Sigma$,以及坐标系的旋转或反射变换 $U$,得到向量 $Ax\in C^m$
如下图所示,原始空间的标准正交基经过坐标系的旋转变换 $V^T$、坐标轴的缩放变换 $\Sigma$、坐标系的旋转变换 $U$ 后,得到与经过线性变换 $A$ 等价的结果
分解方法
根据奇异值分解的定义可推得:
这说明酉矩阵 $U$ 的各列是 $AA^H$ 的标准正交特征向量,称为 $A$ 的左奇异向量(Left Singular Vector),酉矩阵 $V$ 的各列是 $A^HA$ 的标准正交特征向量,称为 $A$ 的右奇异值向量(Right Singular Vector)
由此,可得求矩阵的奇异值分解的一种方法,即分别求出 $AA^H$ 和 $A^HA$ 的标准正交特征向量,然后构造酉矩阵 $U$ 和酉矩阵 $V$
需要注意的是,此时需要验证
是否成立,若成立,则得到 $A$ 的奇异值分解
实例
由于
的四个特征值分别为 $\lambda_1=1,\lambda_2=3,\lambda_3=\lambda_4=0$,对应的特征向量分别为
由于这些特征向量均已正交,无需再进行 Schmidt 正交化,将它们单位化后即可得正交阵
又
的三个特征值为 $\mu_1=1,\mu_2=3,\mu_3=0$,对应的特征向量分别为
由于这些特征向量均已正交,无需再进行 Schmidt 正交化,将它们单位化后即可得正交阵
经验证,可得 $A$ 的奇异值分解为
【紧凑形式与截断形式】
紧奇异值分解
奇异值分解的紧凑形式被称为紧奇异值分解(Compact Singular Value Decomposition),其是与原始矩阵等秩的奇异值分解
设 $A\in R^{m\times n},\text{rank } A=r>0$,则称 $U_r\Sigma_rV_r^T$ 为 $A$ 的紧奇异值分解,即:
其中,$U_r$ 为 $m\times r$ 阶矩阵,由完全奇异值分解 $U$ 中的前 $r$ 列得到,$V_r$ 为 $n\times r$ 阶矩阵,由完全奇异值分解 $V$ 中的前 $r$ 列得到,$\Sigma_r=\text{diag }(\sigma_1,\sigma_2,\cdots,\sigma_r)$,$\sigma_1\geq \sigma_2\geq \cdots \geq \sigma_r>0$ 为 $A$ 的 $r$ 个正奇异值
上例给出的原始矩阵 $A$ 的秩为 $2$
那么,$A$ 的紧奇异值分解为:
其中,$U_r,\Sigma_r,V_r$ 分别为:
截断奇异值分解
奇异值分解的截断形式被称为截断奇异值分解(Truncated Singular Value Decomposition),其是比原始矩阵低秩的奇异值分解,只取奇异值分解中最大的 $k(k<r)$ 个奇异值对应的部分
设 $A\in R^{m\times n},\text{rank } A=r>0$,且 $0<k<r$,则称 $U_k\Sigma_kV_k^T$ 为 $A$ 的截断奇异值分解,即:
其中,$U_k$ 为 $m\times k$ 阶矩阵,由完全奇异值分解 $U$ 中的前 $k$ 列得到,$V_k$ 为 $n\times k$ 阶矩阵,由完全奇异值分解 $V$ 中的前 $k$ 列得到,$\Sigma_k=\text{diag }(\sigma_1,\sigma_2,\cdots,\sigma_k)$,$\sigma_1\geq \sigma_2\geq \cdots \geq \sigma_k>0$ 为 $A$ 的 $k$ 个正奇异值
上例给出的原始矩阵 $A$ 的秩为 $2$
若取 $k=1$,那么,$A$ 的截断奇异值分解为:
其中,$U_1,\Sigma_1,V_1$ 分别为:

