流形学习

【概述】

流形学习（Manifold Learning）是一类借鉴拓扑流形概念的降维方法

流形是指在局部与欧氏空间同胚的空间，即其在局部具有欧氏空间的性质，能用欧氏距离来进行距离计算

若低维流形嵌入到高维空间中，则数据样本在高维空间的分布虽然看起来十分复杂，但在局部上仍具有欧氏空间的性质

因此，可以容易地在局部建立降维映射关系，然后再设法将局部映射关系推广到全局

【等距特征映射】

测地线距离

等距特征映射（Isometric Mapping，ISOMAP）的基本出发点，是认为低维流形嵌入到高维空间之后，直接在高维空间中计算直线距离具有误导性，即高维空间中的直线距离在低维嵌入流形上是不可达的

如下图所示，图中的黑色直线是高维空间中的直线距离，红色曲线是空间中两点的最短距离，其被称为测地线距离（Geodesic）

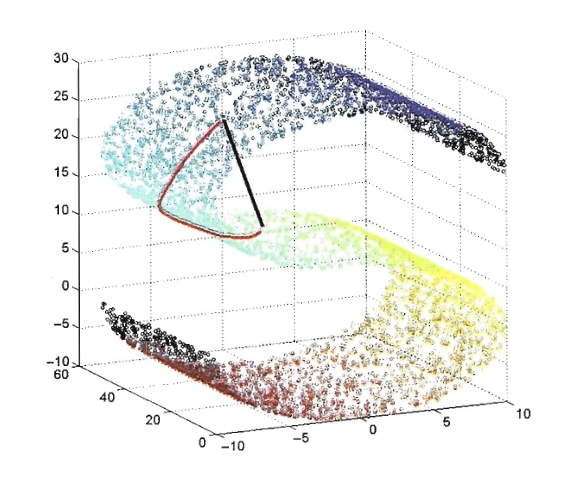
基本思想

显然，低维嵌入流形上的测地线距离不能用高维空间的直线距离计算，但可以利用流形在局部上与欧氏空间同胚这个性质，对每个点基于欧氏距离找出其近邻点，然后建立一个近邻图，图中的近邻点间存在连接，而非近邻点间不存在连接

对近邻图的构建通常有两种做法：

• 指定近邻点个数 $k$，得到 $k$ 近邻图
• 指定距离阈值 $\varepsilon$，距离小于 $\varepsilon$ 的点被认为是近邻点，得到 $\varepsilon$ 近邻图

如下图所示，基于近邻距离逼近能够获得低维流形上测地线距离很好的近似

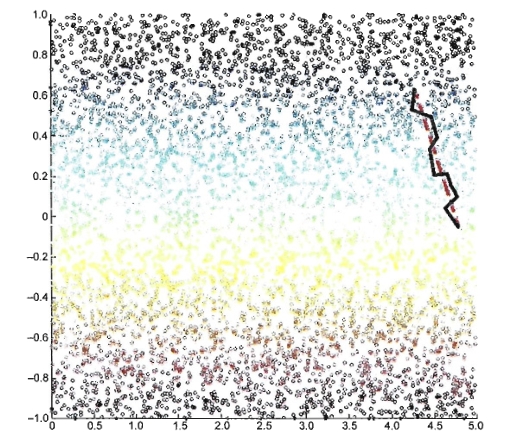
在近邻图建立完毕后，计算两点之间测地线距离的问题，就转变为计算近邻连接图上两点之间的最短路径问题

而在近邻连接图上计算两点间的最短路径，可采用 Dijkstra 算法或 Floyd 最短路算法，在得到任意两点的距离之后，就可通过多尺度比变换 MDS 的方法来获得样本点在低维空间中的坐标

需注意的是，ISOMAP 仅是得到了训练样本在低维空间的坐标，对于新样本，若要将其映射到低维空间通常是将训练样本的高维空间坐标作为输入、低维空间坐标作为输出，训练一个回归学习器来对新样本的低维空间坐标进行预测

算法流程

输入：样本集 $D=\{\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n\}$，第 $i$ 个样本的输入 $\mathbf{x}_i$ 具有 $m$ 个特征值，即：$\mathbf{x}_i = (x_i^{(1)},x_i^{(2)},\cdots,x_i^{(m)})\in \mathbb{R}^{m}$；近邻参数 $k$ 或距离阈值 $\varepsilon$；降维到的维度 $d$

输出：降维后的数据集 $D’=\{\mathbf{z}_1,\mathbf{z}_2,\cdots,\mathbf{z}_n\}$，第 $i$ 个样本的输入 $\mathbf{z}_i$ 具有 $d$ 个特征值，即：$\mathbf{z}_i = (z_i^{(1)},z_i^{(2)},\cdots,z_i^{(d)})\in \mathbb{R}^{d}$，

算法流程：

Step1：对每个样本 $\mathbf{x}_i$，根据近邻参数 $k$ 或距离阈值 $\varepsilon$ 确定近邻图，并将 $\mathbf{x}_i$ 与近邻间的距离设置为欧氏距离，与其他点的距离设为无穷大

Step2：使用最短路径算法 Dijkstra 或 Floyd 计算任意两样本 $\mathbf{x}_i$ 和 $\mathbf{x}_j$ 间的距离 $\text{dist}(\mathbf{x}_i,\mathbf{x}_j)$

Step3：将 $\text{dist}(\mathbf{x}_i,\mathbf{x}_j)$ 作为多尺度变换 MDS 算法的输入

Step4：通过多尺度变换 MDS 算法，得到降维后的数据集 $D’=\{\mathbf{z}_1,\mathbf{z}_2,\cdots,\mathbf{z}_n\}$

【局部线性嵌入】

基本思想

局部线性嵌入（Locally Linear Embedding，LLE）希望在降维后的低维空间中依然能保持高维空间中的线性关系，其不同于 ISOMAP 通过建立邻接图来保留全局结构，而是从局部结构出发对数据进行降维

在 LLE 方法主要从如下两个基本假设出发：

• 一个流形的局部可以近似于一个欧式空间
• 每个样本均可以利用其近邻进行线性重构

如下图所示，假设样本点 $\mathbf{x}_i$ 的坐标能通过它的领域样本 $\mathbf{x}_j,\mathbf{x}_k,\mathbf{x}_l$ 的坐标通过线性组合而重构出来，即使得下式线性重构的关系在低维空间中得以保持

$$\mathbf{x}_i = w_{ij}\mathbf{x}_j + w_{ik}\mathbf{x}_k+w_{il}\mathbf{x}_l$$

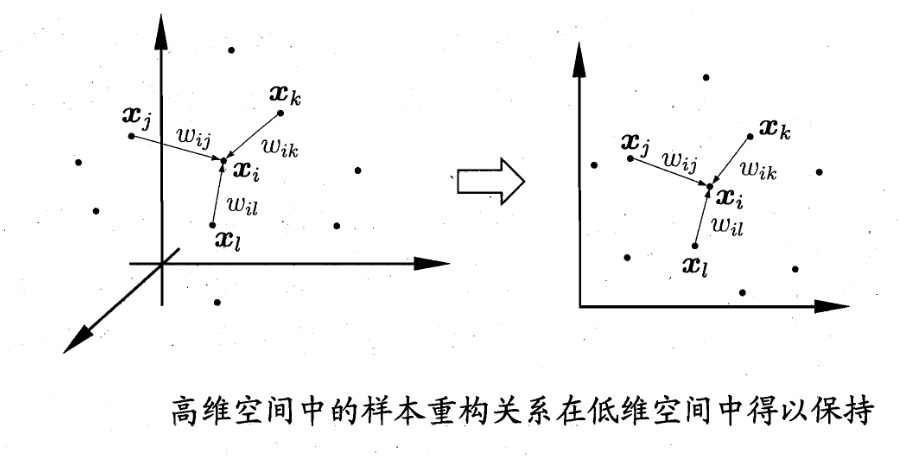
具体来说，对于样本集 $D=\{\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n\}$，第 $i$ 个样本的输入 $\mathbf{x}_i$ 具有 $m$ 个特征值

LLE 为每个样本 $\mathbf{x}_i$ 找到其近邻集合 $Q_i$，然后计算出基于 $Q_i$ 中的样本点对 $\mathbf{x}_i$ 进行线性重构的系数 $\mathbf{w}_i$，即：

$$\begin{gather*} \min_{\mathbf{w}_1,\mathbf{w}_2,\cdots,\mathbf{w}_n} \sum_{i=1}^n \Bigg|\Bigg| \mathbf{x}_i-\sum_{j\in Q_i} w_{ij} \mathbf{x}_j \Bigg|\Bigg|_2^2 \\ s.t. \sum_{j\in Q_i} w_{ij}=1 \end{gather*}$$

由于 $\mathbf{x}_i,\mathbf{x}_j$ 均为已知，那么令：

$$C_{jk} = (\mathbf{x}_i-\mathbf{x}_j)^T(\mathbf{x}_i-\mathbf{x}_k)$$

则有闭式解：

$$w_{ij} = \frac{\sum\limits_{k\in Q_i}C_{jk}^{-1}}{\sum\limits_{l,s\in Q_i}C_{ls}^{-1}}$$

进一步，由于 LLE 在低维空间中保持 $\mathbf{w}_i$ 不变，于是 $\mathbf{x}_i$ 对应的低维空间坐标 $\mathbf{z}_i$ 可通过下式求解：

$$\min_{\mathbf{z}_1,\mathbf{z}_2,\cdots,\mathbf{z}_n} \sum_{i=1}^n \Bigg|\Bigg| \mathbf{z}_i-\sum_{j\in Q_i} w_{ij} \mathbf{z}_j \Bigg|\Bigg|_2^2$$

令

$$\begin{gather*} Z = (\mathbf{z}_1,\mathbf{z}_2,\cdots,\mathbf{z}_n) \in \mathbb{R}^{d\times n} \\ W = [w_{ij}]_{n\times n} \end{gather*}$$

则有：

$$M = (I-W)^T(I-W)$$

故而低维空间坐标 $\mathbf{z}_i$ 的求解可重写为：

$$\begin{gather*} \min_{Z} \text{tr}(ZMZ^T) \\ s.t. ZZ^T = I \end{gather*}$$

此时，即可通过特征值分解来求解，$M$ 最小的 $d$ 个特征值对应的特征向量组成的矩阵，即为 $Z^T$

算法流程

输入：样本集 $D=\{\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n\}$，第 $i$ 个样本的输入 $\mathbf{x}_i$ 具有 $m$ 个特征值，即：$\mathbf{x}_i = (x_i^{(1)},x_i^{(2)},\cdots,x_i^{(m)})\in \mathbb{R}^{m}$；近邻参数 $k$；降维到的维度 $d$

输出：降维后的数据集 $D’=\{\mathbf{z}_1,\mathbf{z}_2,\cdots,\mathbf{z}_n\}$，第 $i$ 个样本的输入 $\mathbf{z}_i$ 具有 $d$ 个特征值，即：$\mathbf{z}_i = (z_i^{(1)},z_i^{(2)},\cdots,z_i^{(d)})\in \mathbb{R}^{d}$，

算法流程：

Step1：对每个样本 $\mathbf{x}_i$，根据近邻参数 $k$ 确定 $k$ 近邻，并求得 $W = [w_{ij}]_{n\times n}$，即

$$\left\{\begin{array}{cc} w_{ij}, & j\in Q_i\\ w_{ij}=0 & j\notin Q_i \end{array}\right.$$

Step2：计算矩阵 $M$

$$M = (I-W)^T(I-W)$$

Step3：对矩阵 $M$ 进行特征值分解

Step4：$M$ 最小的 $d$ 个特征值对应的特征向量组成的矩阵，即为 $Z^T$，故有

$$Z = (\mathbf{z}_1,\mathbf{z}_2,\cdots,\mathbf{z}_n)$$