【概述】
概率图模型(Probabilistic Graphical Model)是一类用图来表达变量相关关系的概率模型
概率图模型以图为表示工具,用一个结点表示一个或一组随机变量,结点之间的边表示变量间的概率相关关系,即变量关系图
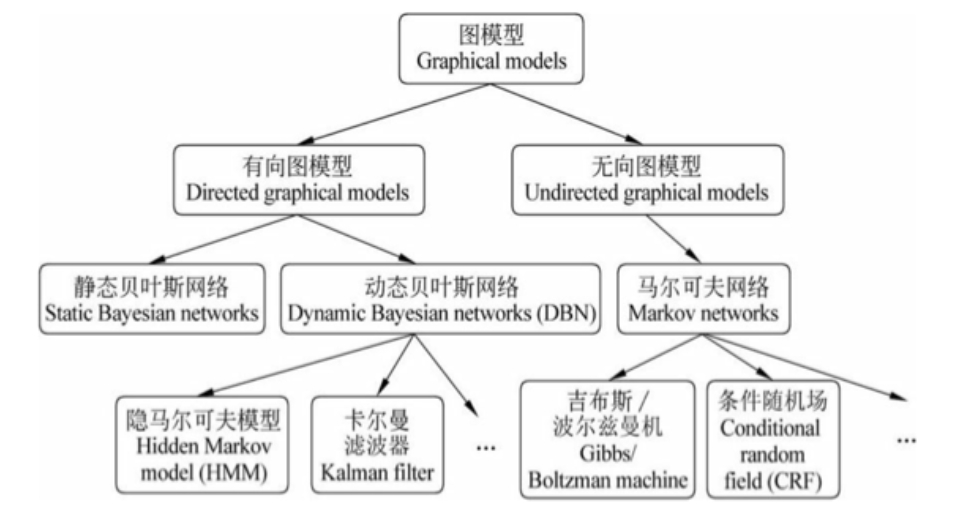
根据边的性质不同,概率图模型可大致分为两类:
- 有向图模型:即贝叶斯网络(Bayesian Network),使用有向无环图表示变量间的依赖关系,常见的模型有贝叶斯网络、隐马尔可夫模型
- 无向图模型:即马尔可夫网络(Markov Network),使用无向图表示变量间的相关关系,常见的模型有概率无向图模型有马尔可夫随机场、条件随机场等
通常来说,若变量间存在显式的因果关系,则使用贝叶斯网络,若变量间存在相关性,但难以获得显式的因果关系,则使用马尔可夫网络
【学习与推断】
对于基于概率图模型定义的联合概率分布,能够通过对目标变量的边际分布或以某些可观测变量为条件的条件分布进行推断
例如在隐马尔可夫模型中,要估算观测序列 $x$ 在给定参数 $\lambda$ 下的条件概率分布,又例如在马尔可夫网中,变量的联合分布被表示为极大团的势函数乘积
于是,在给定参数 $\Theta$ 求解某个变量 $x$ 的分布,就变成对联合分布中其他无关变量进行积分的过程,即边际化(Marginalization)
此外,概率图模型来说,还需确定具体分布的参数,这被称为学习问题或参数估计问题,通常使用极大似然估计或最大后验概率估计求解,但若将参数视为待推断的变量,那么参数估计过程与推断十分相似
具体来说,假设概率图模型所对应的变量集 $\mathbf{x}=\{x_1,x_2,\cdots,x_n\}$ 能分为 $\mathbf{x}_E$ 和 $\mathbf{x}_F$ 两个不相交的变量集,推断问题的目标就是计算边际概率 $P(\mathbf{x}_F)$ 或条件概率 $P(\mathbf{x}_F|\mathbf{x}_E)$
根据条件概率的定义,有:
其中,联合概率 $P(\mathbf{x}_E,\mathbf{x}_F)$ 可基于概率图模型获得,因此,推断问题的关键,就是如何高效计算边际分布,即:
【推断方法】
概率图模型的推断方法大致可分为两类:
- 精确推断方法
- 近似推断方法
对于精确推断方法来说,其目标是计算出目标变量的边际分布或条件分布的精确值,其实质是一类动态规划算法,通过图模型所描述的条件独立性来削减计算目标概率所需的计算量,但一般情形下,该类算法的计算复杂度随着极大团规模的增长呈指数增长,适用范围有限
而近似推断方法在现实任务中更常用,即在较低的时间复杂度下获得原问题的近似解,常用的近似推断方法有 MH 算法、吉布斯采样法、变分推断等

