【概述】
概率无向图模型(Probabilistic Undirected Graphical Model)又称马尔可夫随机场(Markov Random Field),其是由无向图 $G=(V,E)$ 来表示的联合概率分布 $P(Y)$,其中 $Y\in\mathcal{Y}$ 是一组随机变量,用结点 $v\in V$ 表示随机变量,边 $e\in E$ 表示随机变量间的依赖关系
直观来看,马尔可夫链是下一结点的状态只与当前结点有关系,与过去的结点没有关系,而马尔可夫随机场,是当前结点只与该结点直接连接的结点有关系,与随机场中其他的结点没有关系
在实际应用中,更关心的是如何求联合概率分布 $P(Y)$,即对于给定的马尔可夫随机场,希望将整体的联合概率写成若干子联合概率的乘积,即将联合概率进行因子分解,以便于模型的学习与计算
【形式定义】
定义
设有一组随机变量 $Y\in \mathcal{Y}$,联合概率分布为 $P(Y)$,由无向图 $G=(V,E)$ 来表示,用结点 $v\in V$ 表示一个随机变量 $Y_v,Y=(Y_v)_{v\in V}$,用边 $e\in E$ 表示随机变量间的概率依赖关系,若联合概率分布 $P(Y)$ 满足成对、局部或全局马尔可夫性,就称该联合概率分布为概率无向图模型或马尔可夫随机场
马尔可夫性
1)成对马尔可夫性(Pairwise Markov Property)
设 $u,v$ 是无向图 $G$ 中任意两个没有边连接的结点,结点 $u$ 和 $v$ 分别对应随机变量 $Y_u$ 和 $Y_v$,记其他所有结点为 $O$,对应的随机变量组为 $Y_O$
成对马尔可夫性是指给定随机变量组 $Y_O$ 的条件下,随机变量 $Y_u$ 和 $Y_v$ 是独立的,即:
2)局部马尔可夫性(Local Markov Property)
设 $v\in V$ 是无向图 $G$ 中任意一个结点,对应的随机变量是 $Y_v$,$W$ 是与 $v$ 有边连接的所有结点,对应的随机变量组是 $Y_W$,$O$ 是 $v$ 和 $W$ 外的其他所有结点,对应的随机变量组是 $Y_O$
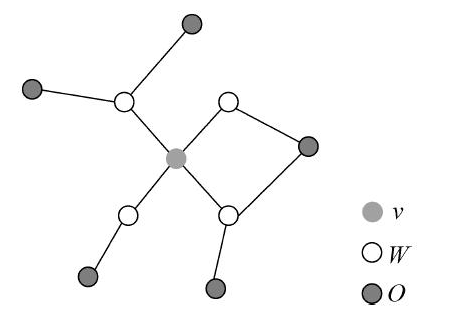
局部马尔可夫性是指给定随机变量组 $Y_W$ 的条件下,随机变量 $Y_v$ 与随机变量组 $Y_O$ 是独立的,即:
在 $P(Y_O|Y_W)>0$ 时,等价地有:
3)全局马尔可夫性(Global Markov Property)
设结点集合 $A,B$ 是无向图 $G$ 中被结点集合 $C$ 分开的任意结点集合,三个结点集合对应的随机变量组分别是 $Y_A,Y_B,Y_C$
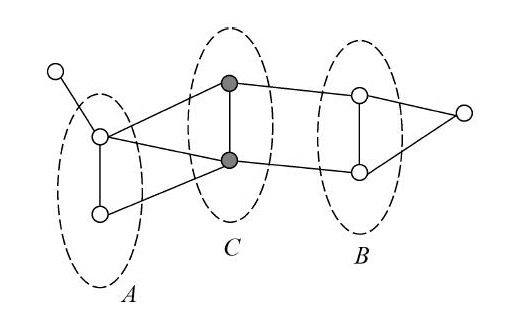
全局马尔可夫性是指给定随机变量组 $Y_C$ 条件下,随机变量组 $Y_A$ 和 $Y_B$ 是条件独立的,即:
【马尔可夫随机场的因子分解】
无向图中的团与最大团
无向图 $G=(V,E)$ 中任何两个结点均有边连接的结点子集,称为团(Clique)
若 $C$ 是无向图 $G$ 中的一个团,且无法再加入任何一个 $G$ 中的结点 $v\in V$ 使其成为一个更大的团,则称 $C$ 为最大团(Maximal Clique)
如下图所示,图中由 $2$ 个结点组成的团有五个:$\{Y_1,Y_2\}$、$\{Y_2,Y_3\}$、$\{Y_3,Y_4\}$、$\{Y_4,Y_2\}$、$\{Y_1,Y_3\}$,有两个最大团 $\{Y_1,Y_2,Y_3\}$、$\{Y_2,Y_3,Y_4\}$
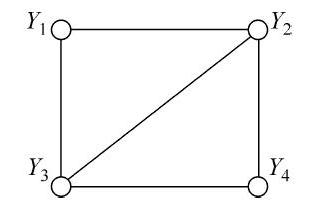
Hammersley-Clifford 定理
马尔可夫随机场的联合分布概率 $P(Y)$ 可表示为:
其中,$C$ 是无向图的最大团,$Y_C$ 是 $C$ 的结点对应的随机变量组,$\Psi_C(Y_C)$ 是 $C$ 上定义的严格正函数,乘积是在无向图所有的最大团上进行的
因子分解
将马尔可夫随机场的联合概率分布表示为,其最大团上的随机变量的函数的乘积,称为概率无向图的因子分解(Factorization),其由上述的 Hammersley-Clifford 定理来保证
对给定的马尔可夫随机场,设其无向图为 $G$,$C$ 为 $G$ 上的最大团,$Y_C$ 为 $C$ 对应的随机变量组
那么,马尔可夫随机场的联合概率分布 $P(Y)$ 可写为图中所有最大团 $C$ 上的函数 $\Psi_C(Y_C)$ 的乘积形式,即:
其中,函数 $\Psi_C(Y_C)$ 被称为势函数(Potential Function),用于对团 $C$ 中的变量关系进行建模,要求其是严格正函数,且在所偏好的变量取值上有较大函数值,故通常定义为指数函数,即:
$Z$ 是规范化因子(Normalization factor),其保证了 $P(Y)$ 构成一概率分布,即:

