References:
【引入】
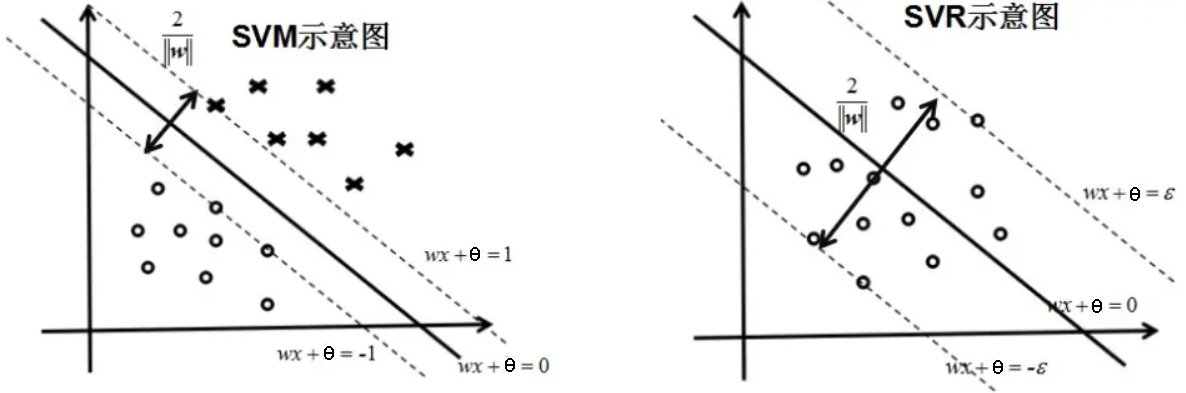
支持向量机是针对二分类问题提出的,其通过最大化间隔来找到一个分离超平面,使得绝大多数样本点位于两个决策边界的外侧
而支持向量回归(Support Vector Regression)是支持向量机的一种改进,用于解决回归问题,其同样是考虑最大化间隔,但是考虑的是两个决策边界之间的点,使尽可能多的样本点位于间隔内
换句话说,SVM 要使超平面到最近的样本点的间隔最大,SVR 则要使超平面到最远的样本点的间隔最小
【假设形式】
对于给定的容量为 $n$ 的训练集 $D=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),…,(\mathbf{x_n},y_n)\}$,第 $i$ 组样本中的输入 $\mathbf{x_i}$ 具有 $m$ 个特征值,即:$\mathbf{x_i}=(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{R}^m$,输出 $y_i\in \mathcal{Y}$,支持向量机学习到的模型为 $f(\mathbf{x})=\boldsymbol{\omega}\cdot \mathbf{x} +\theta$,使得 $f(\mathbf{x_i})\simeq y_i$
假设能容忍 $f(\mathbf{x}_i)$ 与 $y_i$ 间最多有 $\varepsilon$ 的偏差,即仅当 $f(\mathbf{x}_i)$ 与 $y_i$ 之间差距的绝对值大于 $\varepsilon$ 时才计算损失,这相当于以 $f(\mathbf{x})$ 为中心,构建了一个宽度为 $2\varepsilon$ 的间隔带,若训练样本落于该间隔带,则认为预测正确
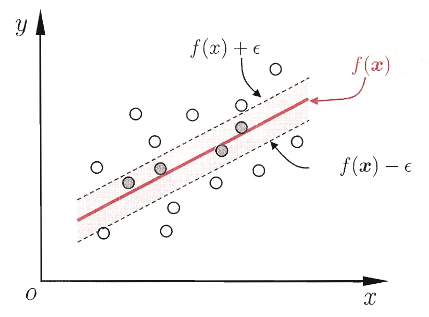
由此,可给出支持向量回归的优化问题:
其中,$\varepsilon>0$ 是间隔带大小
通过求解最优化问题,可以得到超平面:
以及相应的回归函数:
【原始问题】
为每个样本点 $(\mathbf{x}_i,y_i)$ 引入松弛变量 $\xi_i$ 和 $\hat{\xi_i}$,即每个样本点分别到两个决策边界的距离

此时,支持向量回归的优化问题可写为:
即为支持向量回归的原始问题,其中,$C$ 为正则化常数
可以发现,支持向量回归只对间隔外的样本进行惩罚,当样本点位于间隔内,不计算其损失
【对偶问题】
对偶问题的转化
为求解支持向量回归的原始问题:
应用拉格朗日对偶性,通过求解对偶问题来得到原始问题的最优解
首先,构建拉格朗日函数,即为每个不等式约束引入拉格朗日乘子 $\lambda_i\geq0$、$\hat{\lambda_i}\geq 0$、$\mu_i\geq 0$、$\hat{\mu_i}\geq 0$,即:
其中,$\boldsymbol{\lambda}=(\lambda_1,\lambda_2,\dots,\lambda_n)^T$、$\hat{\boldsymbol{\lambda}}=(\hat{\lambda_1},\hat{\lambda_2},\dots,\hat{\lambda_n})^T$、$\boldsymbol{\mu}=(\mu_1,\mu_2,\dots,\mu_n)^T$、$\hat{\boldsymbol{\mu}}=(\hat{\mu_1},\hat{\mu_2},\dots,\hat{\mu_n})^T$ 为拉格朗日乘子向量
此时,根据拉格朗日对偶性,原始问题的对偶问题就变为极大极小问题,即:
因此,为了得到对偶问题的解,就要先求拉格朗日函数 $L(\boldsymbol{\omega},\theta,\boldsymbol{\xi},\boldsymbol{\hat{\xi}},\boldsymbol{\lambda},\boldsymbol{\hat{\lambda}},\boldsymbol{\mu},\boldsymbol{\hat{\mu}})$ 对 $\boldsymbol{\omega}$、$\theta$、$\boldsymbol{\xi}$、$\hat{\boldsymbol{\xi}}$ 的极小,再求对 $\boldsymbol{\lambda}$、$\hat{\boldsymbol{\lambda}}$、$\boldsymbol{\mu}$、$\hat{\boldsymbol{\mu}}$ 的极大
对偶问题中的极小问题
对于对偶问题中的极小问题:
令拉格朗日函数 $L(\boldsymbol{\omega},\theta,\boldsymbol{\xi},\boldsymbol{\hat{\xi}},\boldsymbol{\lambda},\boldsymbol{\hat{\lambda}},\boldsymbol{\mu},\boldsymbol{\hat{\mu}})$ 分别对 $\boldsymbol{\omega}$、$\theta$、$\boldsymbol{\xi}$、$\hat{\boldsymbol{\xi}}$ 求偏导,并令其等于 $0$,即:
可得:
将上式带回拉格朗日函数 $L(\boldsymbol{\omega},\theta,\boldsymbol{\xi},\boldsymbol{\hat{\xi}},\boldsymbol{\lambda},\boldsymbol{\hat{\lambda}},\boldsymbol{\mu},\boldsymbol{\hat{\mu}})$ 中,有:
故有:
对偶问题中的极大问题
对于对偶问题中的极大问题:
即为对偶问题,有:
假设上述的对偶问题对 $\boldsymbol{\lambda}$、$\hat{\boldsymbol{\lambda}}$、$\boldsymbol{\xi}$、$\hat{\boldsymbol{\xi}}$ 的一个解为 $\boldsymbol{\lambda}^* = (\lambda_1^*,\lambda_2^*,\cdots,\lambda_n^*)^T$, $\hat{\boldsymbol{\lambda}}^* = (\hat{\lambda_1}^*,\hat{\lambda_2}^*,\cdots,\hat{\lambda_n}^*)^T$、$\boldsymbol{\xi}^* = (\xi_1^*,\xi_2^*,\cdots,\xi_n^*)^T$, $\hat{\boldsymbol{\xi}}^* = (\hat{\xi_1}^*,\hat{\xi_2}^*,\cdots,\hat{\xi_n}^*)^T$、
可以发现,对偶问题满足 KKT 条件,即:
故而有:
可以看出,当且仅当 $(\boldsymbol{\omega}\cdot\mathbf{x}+\theta)-y_i -\varepsilon-\xi_i^* =0$ 时,$\lambda_i^*$ 可取非零值,当且仅当 $(\boldsymbol{\omega}\cdot\mathbf{x}+\theta)-y_i -\varepsilon-\hat{\xi_i}^* =0$ 时,$\hat{\lambda_i}^*$ 可取非零值,换言之,仅当样本 $(\mathbf{x}_i,y_i)$ 不落于 $\varepsilon$ 间隔带时,相应的 $\lambda_i$ 和 $\hat{\lambda_i}$ 才可取非零值
此外,约束 $(\boldsymbol{\omega}\cdot\mathbf{x}+\theta)-y_i -\varepsilon-\xi_i^* =0$ 和 $(\boldsymbol{\omega}\cdot\mathbf{x}+\theta)-y_i -\varepsilon-\hat{\xi_i}^* =0$ 不能同时成立,否则有 $\xi_i^*=\hat{\xi_i^*}=\varepsilon$,因此 $\lambda_i$ 和 $\hat{\lambda_i}$ 中至少有一个为零,即 $\lambda_i\hat{\lambda_i}$
而对于每个样本 $(\mathbf{x}_i,y_i)$,都有 $(C-\lambda_i^*)\xi_i^* = 0$ 且 $(\boldsymbol{\omega}\cdot\mathbf{x}+\theta)-y_i -\varepsilon-\xi_i^* =0$,于是在得到 $\lambda_i^*$ 后,若存在 $0<\lambda_i^*<C$,那么必有 $\xi_i^*=0$,进而对此 $i$ 有:
理论上来说,可以任意选取满足 $0<\lambda_i^*<C$ 的样本,通过上式得到 $\theta$,但在实际应用中,常选取所有的满足 $0<\lambda_i^*<C$ 的样本,求取相应的 $\theta$ 后求其平均值 $\overline{\theta}$
故而,当 $\lambda_i-\hat{\lambda_i}\neq0$ 时,有回归函数:
【非线性支持向量回归】
对于回归函数:
若考虑到非线性问题,可以参照非线性支持向量机的思路,使用核方法进行特征构建,引入核函数即可,故非线性 SVR 可表示为:
关于核函数,详见:特征构建与核方法
【sklearn 实现】
线性支持向量回归
以 sklearn 中的波士顿房价数据集为例,实现线性支持向量回归
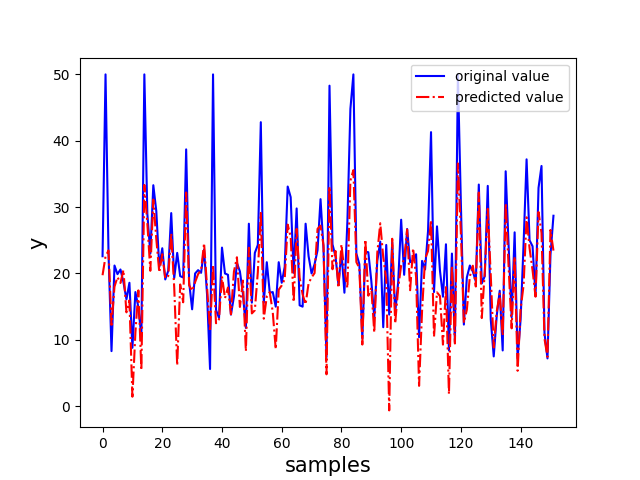
1 | import numpy as np |
非线性支持向量回归
以 sklearn 中的波士顿房价数据集为例,实现线性支持向量回归

1 | import numpy as np |

