References：

• 贝叶斯网络，看完这篇我终于理解了(附代码)！
• 概率图模型之贝叶斯网络
• 机器学习之贝叶斯网络
• 贝叶斯网络(Bayesian Network)

【贝叶斯网络】

贝叶斯网络（Bayesian Network）借助 DAG 来刻画特征间的依赖关系，并使用条件概率表（Conditional Probability Table，CPT）来描述特征的联合概率分布

一般而言，一个贝叶斯网络 $B$ 由结构 $G$ 与参数 $\Theta$ 来表示，即 $B= < G,\Theta >$

其中，结构 $G$ 是一个 DAG，其中每个结点对应一个特征，若两个特征间存在依赖关系，则根据依赖关系建立一条有向边；参数 $\Theta$ 描述了依赖关系，假设特征 $x^{(j)}$ 在结构 $G$ 中的父结点集为 $\pi^{(j)}$，则 $\Theta$ 包含了每个特征的条件概率表，即

$$\Theta_{x^{(j)}|\pi^{(j)}}=P_B(X^{(j)}=x^{(j)}|\pi^{(j)})$$

【条件独立性】

对于贝叶斯网络来说，由于其是一个图结构，因此若每两个特征结点都存在一条边，那么所构建的贝叶斯网络将是一个全连接 DAG，这就意味着模型十分复杂，可能会出现过拟合

为避免过拟合的发生，贝叶斯网络假设每个特征结点与其非子结点独立，由此有效地表达了特征间的条件独立性

也就是说，贝叶斯网络 $B= < G,\Theta >$ 将特征 $X^{(1)},X^{(2)},…,X^{(n)}$ 的联合概率分布定义为：

$$P_B(X^{(1)}=x^{(1)},...,X^{(n)}=x^{(n)}) = \prod_{i=1}^n P(X^{(i)}=x^{(i)}|X^{(i+1)}=x^{(i+1)},...,X^{(n)}=x^{(n)})$$

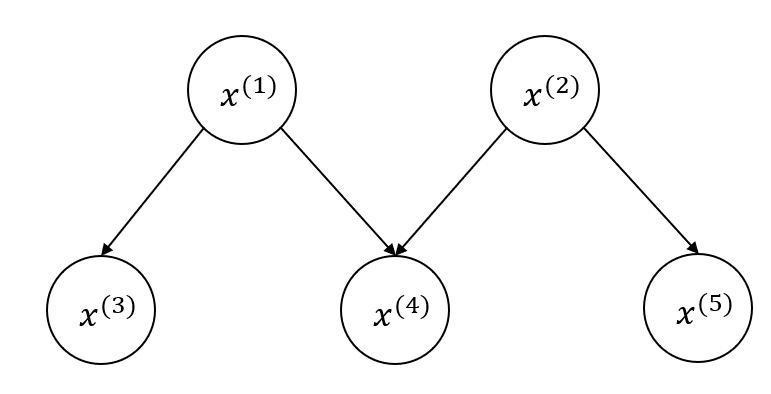
如上图，联合概率分布表示为：

$$P(x^{(1)},x^{(2)},x^{(3)},x^{(4)},x^{(5)})=P(x^{(1)})P(x^{(2)})P(x^{(3)}|x^{(1)})P(x^{(4)}|x^{(1)},x^{(2)})P(x^{(5)}|x^{(2)})$$

显然，在给定 $x^{(1)}$ 的情况下，$x^{(3)}$ 和 $x^{(4)}$ 独立；在给定 $x^{(2)}$ 的情况下，$x^{(4)}$ 和 $x^{(5)}$ 独立

此时，可以简记为：

$$\begin{matrix} x^{(3)}\perp x^{(4)}|x^{(1)} & x^{(4)}\perp x^{(5)}|x^{(2)} \end{matrix}$$

【独立性结构】

同父结构

同父结构（Common parent structure），又称尾对尾结构（Tail-to-tail Structure）

其在给定父特征 $x^{(1)}$ 的取值下，其将子特征结点 $x^{(2)}$ 和 $x^{(3)}$ 阻断（Blocked）， $x^{(2)}$ 和 $x^{(3)}$ 彼此条件独立

顺序结构

顺序结构（Sequence Structure），又称头对尾结构（Head-to-tail Structure）

其在给定子特征 $x^{(2)}$ 的取值下，其将父特征结点 $x^{(1)}$ 与其子特征结点 $x^{(3)}$ 阻断（blocked）， $x^{(1)}$ 和 $x^{(3)}$ 彼此条件独立

但若

V 型结构

V 型结构（V-structure），又称头对头结构（Head-to-Head Structure）

其在给定子特征 $x^{(3)}$ 的取值下，父特征结点 $x^{(1)}$ 和 $x^{(2)}$ 必不独立；但若子特征 $x^{(3)}$ 的取值未知， $x^{(1)}$ 和 $x^{(2)}$ 却是独立的

【边际独立性】

在 V 型结构中，子特征的取值确定与否，会对其两个父特征的独立性发生影响

简单来说，当 $x^{(3)}$ 发生时， $x^{(1)}$ 发生与否与 $x^{(2)}$ 发生与否是无关的，即：

$$\begin{align*} P(x^{(1)},x^{(2)}) &= \sum_{x^{(3)}}P(x^{(1)},x^{(2)},x^{(3)}) \\ &= \sum_{x^{(3)}}P(x^{(3)}|x^{(1)},x^{(2)})P(x^{(1)})P(x^{(2)}) \\ &= P(x^{(1)})P(x^{(2)}) \end{align*}$$

这种情况，被称为边际独立性（Marginal Independence），记为：$x^{(1)}\amalg x^{(2)}$

实际上，这种情况并非 V 型结构所独有，例如在同父结构中，条件独立性 $x^{(2)}\perp x^{(3)}|x^{(1)}$ 成立，但若 $x^{(1)}$ 的取值未知，则边际独立性 $x^{(2)}\amalg x^{(3)}$ 不成立

【条件独立性分析】

为分析 DAG 中的条件独立性，使用有向分离（Directed Separation），将有向图转为无向图，其步骤如下：

1. 找出有向图中所有的 V 型结构
2. 在所有的 V 型结构的两个父结点间加一条无向边
3. 将所有有向边改为无向边

由此产生的无向图称为道德图（Moral graph），其含义是子结点的父结点间应该建立牢靠的关系，否则是不道德的，由此，令父结点相连接的过程，称为道德化（Moralization）

假定道德图中存在变量 $x$ 与 $y$，以及变量集合 $z=\{z_i\}$，若变量 $x$ 与 $y$ 在图上可被变量集合 $z$ 分开，即将 $z$ 去除后 $x$ 与 $y$ 分属两连通分支，则称为变量 $x$ 与 $y$ 被变量集合 $z$ 有向分离， 条件独立关系 $x\perp y|z$ 成立

如上图所示，在上图的道德图中，可以轻易的找出所有的条件独立关系：

$$\begin{matrix} x^{(3)}\perp x^{(2)}|x^{(1)} & x^{(5)}\perp x^{(1)}|x^{(2)} \\ x^{(3)}\perp x^{(4)}|x^{(1)} & x^{(5)}\perp x^{(3)}|x^{(2)} \\ x^{(3)}\perp x^{(5)}|x^{(1)} & x^{(5)}\perp x^{(4)}|x^{(2)} \end{matrix}$$

【贝叶斯网络中的马尔可夫毯】

在随机变量的全集 $U$，对于给定的变量 $X\in U$ 和变量集 $MB\subset U,X\notin MB$，如果满足：

$$X\perp \{U-MB-\{X\}\} | MB$$

则称满足上述条件的最小变量集 $MB$ 为变量 $X$ 的马尔可夫毯（Markov Blanket）

---

在贝叶斯网络中，一个结点的马尔可夫毯是一个结点集，在这个集合中的结点在给定的条件下，条件独立于其他所有结点

简单来说，一个结点的马尔可夫毯是它的父结点、子结点、兄弟结点

如下图，结点 $T$ 的马尔可夫毯为：$MB(T)=\{x^{(1)},x^{(2)},x^{(4)},x^{(6)},x^{(7)}\}$

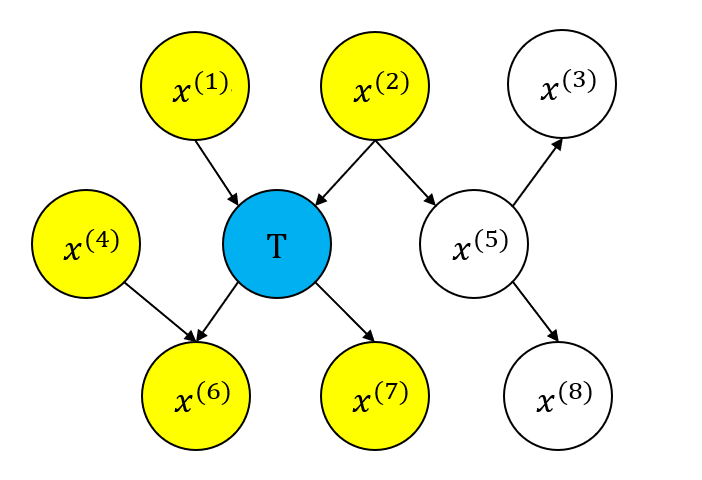
马尔可夫毯是用于特征选择的一种冗余性分析工具，对于目标特征来说，其马尔可夫毯包含了该特征的所有信息，非马尔可夫毯则包含了目标特征的冗余特征

因此，通过发现目标特征的马尔可夫毯，可以准确地确定目标特征的冗余特征，从而降低特征空间的维数

也就是说，如果要了解某特征的分布情况，仅需了解其马尔可夫毯的信息即可，不需对整个数据集了解