【概述】

条件随机场（Conditional Random Field）是给定随机变量 $X$ 的条件下，随机变量 $Y$ 的马尔可夫随机场

这里仅介绍定义在线性链上的特殊的条件随机场，即线性随机场（Linear Chain Conditional Random Field），其在机器学习中常用于标注问题

对于条件概率模型 $P(Y|X)$，其中，$X$ 是输入变量，表示需要标注的观测序列，$Y$ 为输出变量，表示标记序列（在隐马尔可夫模型中，称为状态序列）

与马尔可夫随机场相比，条件随机场也是使用团上的势函数定义概率，两者在形式上没有显著区别，但条件随机场处理的是条件概率，马尔可夫随机场处理的联合概率

【形式定义】

条件随机场

设 $X$ 与 $Y$ 是随机变量，$P(Y|X)$ 是在给定 $X$ 的条件下 $Y$ 的条件概率分布，若随机变量 $Y$ 构成一个由无向图 $G=(V,E)$ 表示的马尔可夫随机场，即：

$P(Y_v|X,Y_w,w\neq v) = P(Y_v|X,Y_w,w\sim v)$

对任意结点 $v$ 成立，则称条件概率分布 $P(Y|X)$ 为条件随机场

式中，$w\sim v$ 表示在图 $G=(V,E)$ 中与结点 $v$ 有边连接的所有结点 $w$，$w\neq v$ 表示结点 $v$ 以外的所有结点，$Y_v,Y_u,Y_w$ 为结点 $v,u,w$ 对应的随机变量

线性链条件随机场

在条件随机场的定义中，没有要求 $X$ 与 $Y$ 具有相同的结构，但在实际应用中，一般假设 $X$ 与 $Y$ 具有相同的图结构

线性链条件随机场即如下图所示的线性链的情况，有：

$G=(V=\{1,2,\cdots,n\},E=\{(i,i+1)\}),\quad i=1,2,\cdots,n-1$

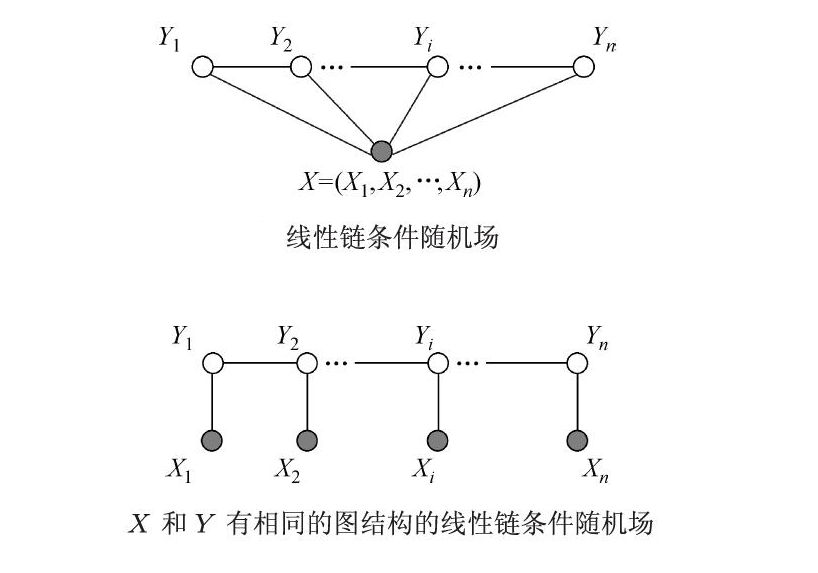
在线性链的情况下，$X=(X_1,X_2,\cdots,X_n),Y=(Y_1,Y_2,\cdots,Y_n)$ 均为线性链表示的随机变量序列，最大团是相邻两结点的集合

若在给定随机变量序列 $X$ 的情况下，随机变量序列 $Y$ 的条件概率分布 $P(Y|X)$ 构成条件随机场，即满足马尔可夫性

$P(Y_i|X,Y_1,Y_2,\cdots,Y_{i-1},Y_{i+1},\cdots,Y_n) = P(Y_i|X,Y_{i-1},Y_{i+1}), \quad i=1,2,\cdots,n$

则称 $P(Y|X)$ 为线性链条件随机场

在标准问题中，$X$ 表示输入观测序列，$Y$ 表示对应的输出标记序列或状态序列，同时将线性链条件随机场简称为条件随机场

【基本形式】

形式

根据 Hammersley-Clifford 定理，可给出线性链条件随机场 $P(Y|X)$ 的因子分解式，各因子是定义在最大团（相邻两结点）上的势函数

设 $P(Y|X)$ 为线性链条件随机场，则在随机变量 $X$ 取值为 $x$ 的条件下，随机变量 $Y$ 取值为 $y$ 的条件概率具有如下形式：

$\begin{align*} P(y|x) &= \frac{1}{Z(x)} \exp \bigg( \sum_{i,k} \lambda_k t_k(y_{i-1},y_i,x,i) + \sum_{i,l} \mu_l s_l (y_i,x,i) \bigg) \\ Z(x) &= \sum_{y} \exp \bigg( \sum_{i,k} \lambda_k t_k (y_{i-1},y_i,x,i) + \sum_{i,l} \mu_l s_l (y_i,x,i) \bigg) \end{align*}$

其中，求和是在所有可能的输出序列上进行的，$Z(x)$ 是规范化因子，其保证 $P(y|x)$ 构成一概率分布

$t_k$ 是定义在边上的局部特征函数，依赖于当前和前一个位置，被称为转移特征，$s_l$ 是定义在结点上的局部特征函数，依赖于当前位置，被称为状态特征，$\lambda_k$ 和 $\mu_l$ 是对应的权值

对于转移特征和状态特征，通常当满足特征条件时取 $1$，否则取 $0$，因此，条件随机场完全由特征函数 $t_k,s_l$ 和对应的权值 $\lambda_k,\mu_l$ 确定

示例

设有一标注问题：输入观测序列为 $X=(X_1,X_2,X_3)$，输出标记序列为 $Y=(Y_1,Y_2,Y_3)$，$Y_1,Y_2,Y_3\in \mathcal{Y}=\{1,2\}$

假设特征函数 $t_1$ 和对应的权值 $\lambda_1$ 为：

$t_1 = t_1(y_{i-1}=1,y_i=2,x,i) = \left\{\begin{array}{bb} 1, & y_{i-1}=1,y_i=2,x,i(i=2,3) \\ 0, & 其他 \end{array}\right. \\$

将特征取值为 $0$ 的条件省略，即有：

$t_1=t_1(y_{i-1}=1,y_i=2,x,i), i=2,3 \quad \lambda_1=1$

以此类推，对于特征函数 $t_k,s_l$ 和对应权值 $\lambda_k,\mu_l$，有：

$\begin{array}{ll} t_1 = t_1(y_{i-1}=1,y_i=2,x,i), i=2,3 && \lambda_1=1 \\ t_2 =t_2(y_1=1,y_2=2,x,2), && \lambda_2=0.6 \\ t_3 =t_3(y_2=2,y_3=1,x,3), && \lambda_3=1 \\ t_4 =t_4(y_1=2,y_2=1,x,2), && \lambda_4=1 \\ t_5 =t_5(y_2=2,y_3=2,x,3), && \lambda_2=0.2 \\ s_1 =s_1(y_1=1,x,1), && \mu_1=1 \\ s_2 =s_2(y_i=2,x,i),i=1,2 && \mu_2=0.5 \\ s_3 =s_3(y_i=1,x,i),i=2,3 && \mu_1=0.8 \\ s_4 =s_4(y_3=2,x,3), && \mu_4=0.5 \\ \end{array}$

对于给定的观测序列 $x$，求：标记序列为 $y=(y_1,y_2,y_3)=(1,2,2)$ 的非规范化条件概率

解：线性链条件随机场模型为：

$P(y|x) \propto \exp \bigg( \sum_{k=1}^5 \lambda_k \sum_{i=2}^3 t_k(y_{i-1},y_i,x,i) + \sum_{k=1}^4 \mu_k \sum_{i=1}^3 s_k (y_i,x,i) \bigg)$

故对给定的观测序列 $x$，标记序列 $y=(1,2,2)$ 的非规范化条件概率为：

$P(y_1=1,y_2=2,y_3=2|x) \propto \exp(3.2)$

【内积形式】

注意到线性链条件随机场中同一特征的各个位置都有定义，故可对同一特征在各个位置求和，将局部特征函数转换为全局特征函数，从而将线性链条件随机场写为权值向量和特征向量的内积形式

设有 $K_1$ 个转移特征，$K_2$ 个状态特征，则总共有 $K=K_1+K_2$ 个特征函数，记：

$f_k(y_{i-1},y_i,x,i) = \left\{\begin{array}{ll} t_k(y_{i-1},y_i,x_i), & k=1,2,\cdots,K_1 \\ s_l(y_{i},x,i), & k=K_1+l;l=1,2,\cdots,K_2 \\ \end{array}\right.$

用 $f_k(y,x)$ 表示转移特征与状态特征在各位置 $i$ 求和，即：

$f_k(y,x) = \sum_{i=1}^n f_k (y_{i-1},y_i,x_i),\quad k=1,2,\cdots,K$

再用 $w_k$ 表示特征 $f_k(y,x)$ 的权值，即：

$w_k = \left\{\begin{array}{ll} \lambda_k, & k=1,2,\cdots,K_1 \\ \mu_l, & k=K_1+l;l=1,2,\cdots,K_2 \\ \end{array}\right.$

则线性链条件随机场可写为：

$\begin{align*} P(y|x) &= \frac{1}{Z(x)} \exp \sum_{k=1}^K w_k f_k(y,x) \\ Z(x) &= \sum_{y} \exp \sum_{k=1}^K w_k f_k(y,x) \end{align*}$

若以 $\mathbf{w}$ 表示权值向量，即：

$\mathbf{w}=(w_1,w_2,\cdots,w_K)^T$

以 $F(y,x)$ 表示全局特征向量，即：

$F(y,x) = (f_1(y,x),f_2(y,x),\cdots,f_K(y,x))^T$

则线性链条件随机场可写为向量 $\mathbf{w}$ 与 $F(y,x)$ 的内积形式，即：

$\begin{align*} P_{\mathbf{w}}(y|x) &= \frac{1}{Z_{\mathbf{w}}(x)} \exp \big[ \mathbf{w}\cdot F(y,x) \big ]\\ Z_{\mathbf{w}}(x) &= \sum_{y} \exp \big[ \mathbf{w} \cdot F(y,x) \big ] \end{align*}$

【矩阵形式】

形式

假设 $P_{\mathbf{w}}(y|x)$ 是由线性链条件随机场，其形式如下：

$\begin{align*} P(y|x) &= \frac{1}{Z(x)} \exp \sum_{k=1}^K w_k f_k(y,x) \\ Z(x) &= \sum_{y} \exp \sum_{k=1}^K w_k f_k(y,x) \end{align*}$

对每个标记序列引进特殊的起点和终点状态标记 $y_0=\text{start}$ 和 $y_{n+1}=\text{stop}$，此时标注序列的概率 $P_{\mathbf{w}}(y|x)$ 可以通过矩阵形式表示并有效计算

对观测序列 $x$ 的每一位置 $i=1,2,\cdots,n+1$，由于 $y_{i-1}$ 和 $y_i$ 在 $m$ 个标记中取值，故可以定义一个 $m$ 阶矩阵随机变量：

$M_i(x) = [M_i(y_{i-1},y_i|x)]$

矩阵随机变量的元素为：

$\begin{align*} M_i(y_{i-1},y_i|x) &= \exp [W_i(y_{i-1},y_i|x)] \\ W_i(y_{i-1},y_i|x) &= \sum_{k=1}^K w_k f_k(y_{i-1},y_i,x,i) \end{align*}$

这样，在给定观测序列 $x$ 时，线性链条件随机场可写为矩阵形式，即：

$\begin{align*} P_{\mathbf{w}}(y|x) &= \frac{1}{Z_{\mathbf{w}}(x)} \prod_{i=1}^{n+1} M_i(y_{i-1},y_i|x) \\ Z_{\mathbf{w}}(x) &= [M_1(x)M_2(x)\cdots M_{n+1}(x)]_{\text{start},\text{stop}} \end{align*}$

其中，相应标记序列 $y$ 的非规范化概率是通过该序列 $n+1$ 个矩阵的适当元素的乘积 $\prod\limits_{i=1}^{n+1} M_i(y_{i-1},y_i|x)$ 来表示，$Z_{\mathbf{w}}(x)$ 是规范化因子，其是 $n+1$ 个矩阵的乘积的 $(\text{start},\text{stop})$ 元素，即以 $\text{start}$ 为起点以 $\text{stop}$ 为终点通过状态的所有路径 $y_1y_2\cdots y_n$ 的非规范化概率 $\prod_{i=1}^{n+1} M_i(y_{i-1},y_i|x)$ 之和

示例

给定一个如下图所示的线性链条件随机场，观测序列 $x$，状态序列 $y,i=1,2,3$，标记 $y_i\in \mathcal{Y}=\{1,2\}$

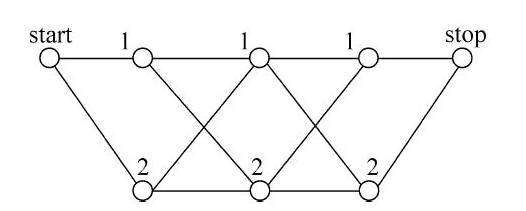
假设 $y_0=\text{start}=1,y_4=\text{stop}=1$，各位置的随机矩阵如下：

$\begin{matrix} M_1(x)=\begin{bmatrix} a_{01} & a_{02} \\ 0 & 0 \end{bmatrix}, & M_2(x)=\begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix}, \\ M_3(x)=\begin{bmatrix} c_{11} & c_{12} \\ c_{21} & c_{22} \end{bmatrix}, & M_4(x)=\begin{bmatrix} 1 & 0 \\ 1 & 0 \end{bmatrix} \\ \end{matrix}$

求：状态序列 $y$ 以 $\text{start}$ 为起点 $\text{stop}$ 为终点所有路径的非规范化概率以及规范化因子

解：对于图中从 $\text{start}$ 到 $\text{stop}$ 对应于 $y=(1,1,1),y=(1,1,2),\cdots,y=(2,2,2)$ 各路径的非规范化概率为

$\begin{matrix} a_{01}b_{11}c_{11} & a_{01}b_{11}c_{12} & a_{01}b_{12}c_{21} & a_{01}b_{12}c_{22} \\ a_{02}b_{21}c_{11} & a_{02}b_{21}c_{12} & a_{02}b_{22}c_{21} & a_{02}b_{22}c_{22} \end{matrix}$

通过计算 $M_1(x)M_2(x)M_3(x)M_4(x)$ 可知，其第一行第一列的元素为：

$\begin{align*} a_{01}b_{11}c_{11} + a_{02}b_{21}c_{11} + a_{01}b_{12}c_{21} + a_{02}b_{22}c_{22}\\ +a_{01}b_{11}c_{12} + a_{02}b_{21}c_{12} + a_{01}b_{12}c_{22}+a_{02}b_{22}c_{21} \end{align*}$

恰好等于从 $\text{start}$ 到 $\text{stop}$ 的所有路径的非规范化概率和，即规范化因子 $Z(x)$

【三个基本问题】

与隐马尔可夫模型类似，线性链条件随机场也存在三个基本问题：

1）概率计算问题

给定线性链条件随机场 $P(Y|X)$，输入序列 $x$ 和输出序列 $y$，计算条件概率 $P(Y_i=y_i|x)$ 和 $P(Y_{i-1}=y_{i-1},Y_i=y_i|x)$，以及相应的数学期望

关于该问题，详见：条件随机场的条件概率计算

2）学习问题

已知线性链条件随机场 $P(Y|X)$，估计 $P(Y|X)$ 的参数

关于该问题，详见：条件随机场的学习

3）预测问题

已知线性链条件随机场 $P(Y|X)$ 和输入序列 $x$，求条件概率最大的输出序列 $y^{*}$，即对输入序列进行标注

关于该问题，详见：条件随机场的预测