Boosting 提升法

References：

• 机器篇——集成学习(三) 细说 提升(Boosting) 算法
• 集成学习-Boosting,Bagging与Stacking
• 梯度提升（Gradient Boosting）算法
• 机器篇——集成学习(五) 细说 梯度提升(Gradient Boost)算法

【Boosting 工作机制】

Boosting 算法（提升算法）是将弱学习器提升为强学习器的一族算法，其基本工作机制是：

1. 从初始训练集中训练出一个弱学习器
2. 根据弱学习器的表现对训练样本分布进行调整，使得先前的弱学习器做错的训练样本在后续受到更多关注
3. 使用基于调整后的样本分布训练下一个弱学习器
4. 重复上述步骤，直到弱学习器达到指定的数目 $T$
5. 将 $T$ 个弱学习器使用结合策略进行结合

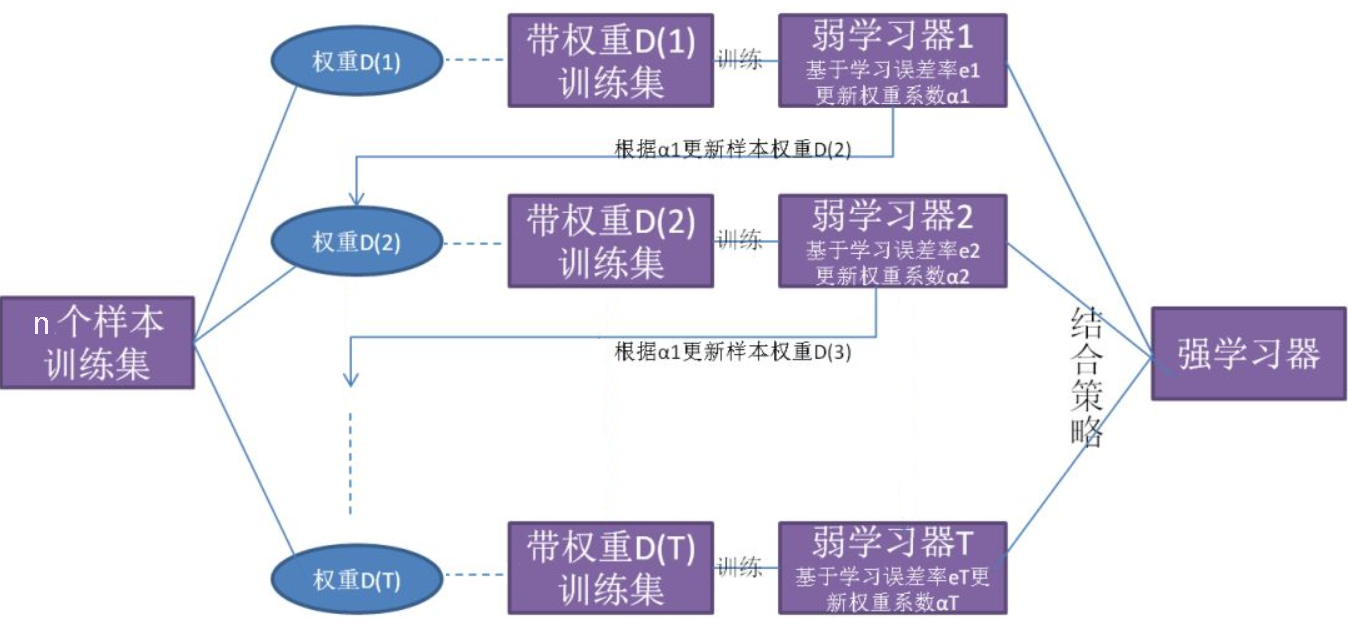
可以发现，与 Bagging 袋装法不同，Boosting 是一种串行结构，整个训练过程呈阶梯状，弱学习器按次序进行训练，训练集每次都按照某种策略进行一定的转化，最后再以某种结合策略将弱学习器组合成一个强学习器

此外，Boosting 中所有的弱学习器可以是不同的学习器，即可以是异质集成，但因为过于复杂，很少会使用不同的弱学习器

【加法模型与前向分步法】

Boosting 提升法主要涉及到两个部分，即加法模型与前向分步法

加法模型

加法模型（Additive Model）是指强学习器是由一系列弱学习器线性相加而成的，即：

$$f(\mathbf{x}) = \sum_{t=1}^T \alpha_t G_t(\mathbf{x})$$

其中，$T$ 是弱学习器的个数，$G_t(\mathbf{x})$ 是每个弱学习器的假设函数，被称为基函数，$\alpha_t$ 是基函数的系数，即每个弱学习器在强学习器中所占的比重

前向分步法

在给定容量为 $n$ 的训练集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_n,y_n)\}$ 和损失函数 $L(y,f(\mathbf{x}))$ 的情况下，学习加法模型 $f(\mathbf{x})$ 就变成了损失函数极小化问题，即：

$$\min_{\alpha_t,G_t} \sum_{i=1}^n L\Big(y_i,\sum_{t=1}^T \alpha_t G_t(\mathbf{x}_i) \Big)$$

前向分步法（Forward Stagewise Algorithm）是专门用于求解这一类优化问题的算法，其基本思想是：基于贪心算法，贪婪的逐步优化，即从前向后进行学习，每一步只学习一个基函数及其系数，逐步逼近优化目标函数

这样一来，前向分步法将同时求解从 $1$ 到 $T$ 的所有参数 $\alpha_t$ 和 $G_t$ 的优化问题，就简化为逐步求解各个 $\alpha_t$ 和 $G_t$ 的优化问题

具体来说，就是每一步优化如下损失函数：

$$\min_{\alpha,G} \sum_{i=1}^n L\Big(y_i,\alpha G(\mathbf{x}_i) \Big)$$

---

下面给出前向分步法的算法流程：

输入：容量为 $n$ 的训练集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_n,y_n)\}$，损失函数 $L(y,f(\mathbf{x}))$ ，基函数集 $\{G(\mathbf{x})\}$

输出：加法模型 $f(\mathbf{x})$

算法流程：

Step1：初始化 $f_0(\mathbf{x})=0$

Step2：对 $t=1,2,\cdots,T$

1）极小化损失函数：

$$(\alpha_t,\boldsymbol{\theta}_t) = \arg\min_{\alpha,G} \sum_{i=1}^n L\Big(y_i,f_{t-1}(\mathbf{x}_i)+\alpha G(\mathbf{x}_i) \Big)$$

得到参数 $\alpha_t$ 和 $G_t$

2）更新：

$$f_t(\mathbf{x}) = f_{t-1}(\mathbf{x}) + \alpha_tG_t(\mathbf{x})$$

Step3：得到加法模型

$$f(\mathbf{x}) = f_T(\mathbf{x}) = \sum_{t=1}^T \alpha_t G_t(\mathbf{x})$$

【梯度提升法】

梯度下降法是在参数空间中，进行最优参数的搜索，最优解 $\boldsymbol{\theta}^*$ 是初始值 $\boldsymbol{\theta}_0$ 迭代 $T$ 次而来的

对于损失函数 $L(\boldsymbol{\theta})$，设 $\boldsymbol{\theta}_0 = \frac{\partial{L(\boldsymbol{\theta})}}{\partial{\boldsymbol{\theta}_0}}$，那么最优解可表示为：

$$\boldsymbol{\theta}^* = \sum_{t=1}^T \alpha_t \Big[- \frac{\partial L(\boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \Big]_{\boldsymbol{\theta}=\boldsymbol{\theta}_{t-1}}$$

其中，$\Big[- \frac{\partial L(\boldsymbol{\theta})}{\partial \boldsymbol{\theta}} \Big]_{\boldsymbol{\theta}=\boldsymbol{\theta}_{t-1}}$ 为 $\boldsymbol{\theta}$ 在 $\boldsymbol{\theta}-1$ 处泰勒展开式的一阶导数

那么，在函数空间中，借鉴梯度下降的思想，可以对最优函数进行搜索，这就是梯度提升法（Gradient Boost）

对于模型 $f(\mathbf{x})$ 的损失函数 $L(y,f(\mathbf{x}))$，为求最优的函数 $f^*(\mathbf{x})$，首先设初始值为：

$$f_0(\mathbf{x}) = G_0(\mathbf{x})$$

与梯度下降法的更新过程一致，假设经过 $T$ 次迭代：

$$G_t(\mathbf{x}) = G_{t-1}(\mathbf{x}) + \alpha_t\triangledown G_t(\mathbf{x})$$

其中，$\triangledown G_t(\mathbf{x})$ 为：

$$\triangledown G_t(\mathbf{x}) = \Big[- \frac{\partial L(y,G(\mathbf{x}))}{\partial G(\mathbf{x})} \Big]_{G(\mathbf{x})=G_{t-1}(\mathbf{x})}$$

得到的最优函数为：

$$f^*(\mathbf{x}) = \sum_{t=1}^T G_t(\mathbf{x})$$

可以看到，梯度上升法在每一轮迭代中，首先计算出当前模型在所有样本上的负梯度 $\triangledown G_t(\mathbf{x})$，然后训练一个新的弱分类器 $G_t(\mathbf{x})$，最终实现对模型的更新

关于梯度下降法，详见：梯度下降法

【Boosting 算法族】

Boosting 并非是一种方法，而是一族算法

具体来说，依据损失函数 $L(y,f(\mathbf{x}))$ 的不同，其可以分为若干具体的算法，常见的有：

算法	模型	基函数	针对 问题	损失函数	学习算法	详见
AdaBoost 自适应提升	加法 模型	$-$	分类 回归	分类：指数损失函数 回归：回归误差率	前向分步法	AdaBoost 自适应提升算法
提升树	加法 模型	决策树	分类 回归	分类：指数损失函数 回归：平方损失函数	前向分步法	提升树
GBDT 梯度提升决策树	加法 模型	决策树	分类 回归	一般损失函数	梯度提升法	GBDT 梯度提升决策树

此外，还有损失函数采用平方损失函数的 L2Boosting 算法、采用对数损失函数的 LogitBoost 算法，GBDT 的优化算法 XGBoost 算法等