梯度下降法

Reference

• 梯度下降法 —— 经典的优化方法
• 梯度下降算法（Gradient Descent)的原理和实现步骤
• 详解梯度下降法（干货篇）
• 什么是梯度下降
• 梯度下降算法原理讲解——机器学习
• 随机梯度下降（stochastic gradient descent，SGD）
• 梯度下降法(Gradient Descent)优化函数的详解（3）小批量随机梯度下降法（mini-batch SGD ）

【概述】

梯度下降法（Gradient Descent）不是一个机器学习算法，而是一种基于搜索的最优化方法，其目的是通过迭代来最小化一个效用函数，是求解无约束优化问题最简单、最经典的方法之一

梯度下降法就好比一个蒙着眼睛的人下山，每次在负梯度最大的方向，向前走一步，走出一步后，比较前后的的落差，若落差小于一定阈值，则认为到达山谷，若落差大于阈值，则继续向前走，直到到达山谷

在机器学习中，绝大多数的机器学习模型都会有一个损失函数，用来衡量机器学习模型的精确度，一般来说，损失函数的值越小，模型的精确度就越高，如果要提高机器学习模型的精确度，就要尽可能的降低损失函数的值，而梯度下降法，就是用来优化损失函数的值的

关于损失函数，详见：机器学习三要素

常见的梯度下降法有：批量梯度下降（Batch Gradient Descent，BGD）、随机梯度下降（Stochastic Gradient Descent，SGD）、小批量梯度下降（Mini-Batch Gradient Descent，MBGD），其中小批量梯度下降法常用于深度学习中进行模型的训练

【梯度】

梯度，实际上就是多变量微分的一般化：

• 单变量函数：梯度就是函数的微分，代表着函数在某个给定点的切线的斜率
• 多变量函数：梯度是一个向量，梯度的方向指出了函数在给定点上升最快的方向

而这就说明了梯度向量法为何需要求梯度，即梯度的反方向就是函数在给定点下降最快的方向，只要沿着这个方向一直走，就能走到最低点或局部最低点

举例来说，对于函数：$J(x,y,z) = 15x + y - 3z$，其梯度为：

$$\bigtriangledown J(x,y,z) = \left \langle \frac{\partial J}{\partial x}, \frac{\partial J}{\partial y}, \frac{\partial J}{\partial z} \right \rangle = \left \langle 15,1,-3 \right \rangle$$

【梯度下降法的一般形式】

首先给出梯度下降法的一般形式：

$$\boldsymbol{\theta_{k+1}}=\boldsymbol{\theta_k} - \alpha \bigtriangledown_k J(\boldsymbol{\theta})$$

该公式的含义为：对于当前点 $\boldsymbol{\theta_k}$，要从这个点走向关于 $\boldsymbol{\theta}$ 的函数 $J(\boldsymbol{\theta})$ 的最小值点，前进的方向是函数 $J(\boldsymbol{\theta})$ 的梯度的反方向，行走一段距离的步长为 $\alpha$，到达的点即为 $\boldsymbol{\theta_k}$

步长 $\alpha$ 在机器学习中又被称为学习率（Learning Rate），意味着可以通过控制 $\alpha$ 来控制每一步走的距离

$\alpha$ 的设置不能太小，太小会导致收敛慢，也不能设置太大，太大会导致错过最优解，通常来说，需要从小到大，分别测试，来选出一个最优解

当我们到达最优点或局部最优点时，其梯度为 $0$，此时无论步长 $\alpha$ 为多大，都不会再进行更新

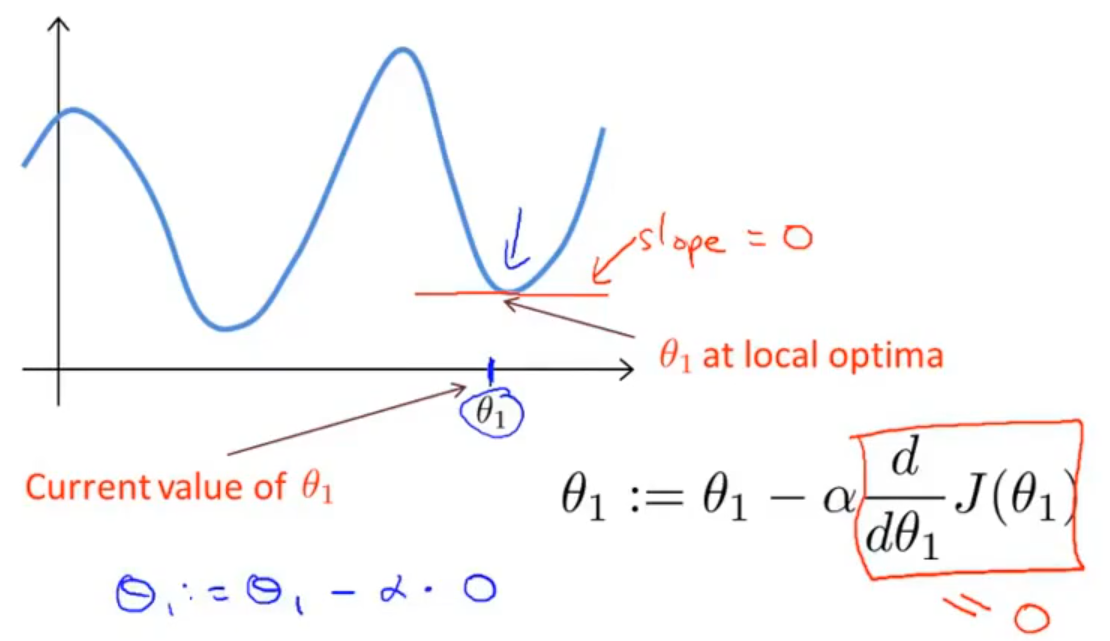
【常见的梯度下降法】

随机梯度下降法 SGD

在上文中所举的例子即随机梯度下降（Stochastic Gradient Descent，SGD），其每次迭代更新时只用到了一个样本来调整

其一般形式为：

$$\begin{align} for & \quad i=1,...,n: \notag \\ &Repeat\:until\:convergence: \notag \\ &\quad \boldsymbol{\theta_{k+1}} = \boldsymbol{\theta_k} - \alpha \big[f(\mathbf{x_i};\boldsymbol{\theta}) -y_i \big] \cdot x_i^{(j)},j = 0,1,...,m \notag \end{align}$$

SGD 从概率意义上来说，单个样本的梯度是对整个数据集合梯度的无偏估计，但是由于存在着一定的不确定性，即下降路径容易受到训练数据自身噪音的影响，因此在每次迭代更新时并不一定是向最优方向进行的

同时，学习率 $\alpha$ 不能设置过大，不然容易在最优解附近出现震荡，始终无法解决最优解，但从另一个角度来看，这种在最优解附近出现震荡的路径，在损失的优化路线在损失函数局部极小值较多时，能够有效避免模型陷入局部最优解

虽然 SGD 不是每次迭代得到的损失函数都向着全局最优方向，但是整体方向是向全局最优解前进的，最终的结果往往是在全局最优解附近，这种方法相比于 BGD 来说，收敛的更快，虽然不是全局最优，但很多时候是可以接受的

批量梯度下降法 BGD

批量梯度下降（Batch Gradient Descent，BGD）认为，对于 $\boldsymbol{\theta}$ 的更新，训练集中的所有样本的损失函数都有贡献，因此，BGD 是计算训练集中所有样本的损失函数的总和后再进行更新，即每一步梯度下降都需要对整个训练集进行处理

其一般形式为：

$$\begin{align} &Repeat\:until\:convergence: \notag \\ &\quad \boldsymbol{\theta_{k+1}} = \boldsymbol{\theta_k} - \alpha \frac{1}{n} \Big[\sum_{i=1}^n \big(f(\mathbf{x_i};\boldsymbol{\theta})-y_i\big) \Big] \cdot x_i^{(j)},j = 0,1,...,m \notag \end{align}$$

BGD 每迭代更新一次参数，都要使用到数据集中的所有样本，其下降方向是最优方向，学习率 $\alpha$ 可以设置的比 SGD 大，但当训练集很大时，由于计算量大，处理速度会比较慢，且不支持在线学习

一般来说，当训练样本数量 $n\leq 2000$ 时，常选用该方法进行优化

小批量梯度下降法 MBGD

小批量梯度下降（Mini-Batch Gradient Descent，MBGD）是为克服 SGD、BGD 两种方法的缺点而出现的，其采用了一种折中手段

MBGD 将数据分为若干批次，按批次更新参数，每一批次中的一组数据共同决定了本次梯度的方向，即每次对训练集进行训练时，只处理 $b$ 个样本

这样下降起来就不容易跑偏，减少了随机性，同时因为每一批的样本数相较整个数据集来说少了很多，计算量也不是很大，在数据量较大的项目中，可以明显地减少梯度计算的时间

其一般形式为：

$$\begin{align} for & \quad i=1,...,n: \notag \\ &Repeat\:until\:convergence: \notag \\ &\quad \boldsymbol{\theta_{k+1}} = \boldsymbol{\theta_k} - \alpha \frac{1}{b} \Big[\sum_{k=i}^{i+b-1} \big(f(\mathbf{x_k};\boldsymbol{\theta})-y_k\big) \Big] \cdot x_k^{(j)},j = 0,1,...,m \notag \\ &\quad i=i+b \notag \end{align}$$

其中，$b$ 为批大小（Batch Size），即选取的样本数量，与计算机的信息存储方式相适应，代码在 $b=2^x$ 时运行速度较快，因此典型的大小为 $2^5,2^6,2^7,2^8,2^9$

一般来说，当训练样本数量 $n\geq 2000$ 时，常选用该方法进行优化

【各梯度下降法的对比】

对于 MBGD 来说，当处理的批次大小 $b=1$ 时，即为 SGD

SGD 每轮对一个训练样本执行一次梯度下降，每一轮训练速度快，但丢失了向量化带来的计算加速，同时其噪声较高，需要适当的减少学习率，代价函数总体趋势向全局最小值靠近，但永远不会收敛，不断的在最小值附近波动

BGD 每轮对所有训练样本执行一次梯度下降，每一轮训练速度慢，但相对来说噪声较低，代价函数总是向减小的方向下降

MBGD 每轮对固定大小的训练样本执行一次梯度下降，每一轮训练速度适中，代价函数总体趋势向全局最小值靠近

BGD 和 MBGD 的代价函数变化趋势如下图：