Alex_McAvoy

想要成为渔夫的猎手

GBDT 梯度提升决策树

发表于 分类于 ，
本文字数： 9k 阅读时长 ≈ 8 分钟

References：

【GBDT 梯度提升决策树】

梯度提升决策树（Gradient Boosting Decision Tree，GBDT）是 Boosting 算法族的一种，其可认为是学习算法采用梯度提升法的提升树

【GBDT 回归算法】

CART 回归树

对于回归问题，设给定的容量为 $n$ 的训练集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_n,y_n)\}$，第 $i$ 组样本中的输入 $\mathbf{x}_i$ 具有 $m$ 个特征值，即：$\mathbf{x}_i=(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{R}^m$，输出 $y_i\in\mathcal{Y}=\{-1,+1\}$

依照 CART 回归树，将输入空间 $\mathcal{X}$ 划分为 $K$ 个互不相交的区域 $R_1,R_2,\cdots,R_K$，并且在每个区域上确定输出的常量 $c_k$，那么决策树可表示为：

其中，$K$ 为回归树的复杂度即叶结点个数，$\{(R_1,c_1),(R_2,c_2),\cdots,(R_K,c_K)\}$ 为树的区域划分和各区域上的最优值

关于 CART 回归树，详见：决策树的 CART 生成算法

梯度提升法

对于梯度提升决策树，使用梯度提升法进行学习，即：

对于梯度提升法的第 $t$ 轮来说，给定当前模型 $G_{t-1}(\mathbf{x})$，需求解：

得到第 $t$ 棵树的参数，即第 $t$ 棵树的区域划分和各区域上的最优值

由于采用梯度提升法，因此只需要简单地拟合当前模型的负梯度 $\triangledown G_t(\mathbf{x}) = \Big[- \frac{\partial L(y,G(\mathbf{x}))}{\partial G(\mathbf{x})} \Big]_{G(\mathbf{x})=G_{t-1}(\mathbf{x})}$ 即可

算法流程

下面给出回归问题的 GBDT 算法的算法流程

输入：容量为 $n$ 的训练集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_n,y_n)\}$，第 $i$ 组样本中的输入 $\mathbf{x}_i$ 具有 $m$ 个特征值，即：$\mathbf{x}_i=(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{R}^m$，输出 $y_i\in\mathcal{Y}\subset \mathbb{R}$

输出：梯度提升树 $f(\mathbf{x})$

Step1：初始化 $G_0(\mathbf{x})$

此时，$c$ 为根结点上的最优值

Step2：对 $t=1,2,\cdots,T$

1）计算负梯度

2）根据 CART 算法，对负梯度 $\triangledown G_{ti}(\mathbf{x}) $ 学习一个回归树，得到树的区域划分 $\{R_{t1},R_{t2},\cdots,R_{tK}\}$

3）根据树的区域划分 $R_{tk}$ ，计算各区域上的最优值 $\{c_{t1},c_{t2},\cdots,c_{tK}\}$

4）更新回归决策树

Step3：根据加法模型得到最终的梯度提升树

【GBDT 分类算法】

分类问题的 GBDT 算法思想上来说与回归问题 GBDT 算法没有区别，但是由于分类问题样本输出不是连续的值，而是离散的类别，这导致无法直接从输出类别去拟合类别输出的误差

为了解决这个问题，主要有两个方法：

  1. 使用指数损失函数：此时 GBDT 算法退化为 AdaBoost 算法
  2. 使用对数损失函数：用类别的预测概率值和真实概率的差来拟合损失

关于 AdaBoost 分类算法，详见：AdaBoost 算法

【GBDT 的正则化】

为防止过拟合，GBDT 与 AdaBoost 一样，需要进行正则化

GBDT 的正则化主要有三种方式：

1）对于梯度上升法的更新 $G_t(\mathbf{x}) = G_{t-1}(\mathbf{x}) + \sum\limits_{k=1}^K c_k \mathbb{I}(\mathbf{x}\in R_{tk})$，有：

其中，$\mu \in (0,1]$ 即为学习率

2）通过子采样（Subsample） 比例限制，取值 $(0,1]$

如果取值为 $1$，则说明使用全部样本，相当于没有采用子采样；如果取值小于 $1$，说明只有一部分样本会进行 GBDT 的决策树拟合

需要注意的是，这里的子采样和随机森林不一样，随机森林使用的是有放回抽样，而这里是不放回抽样

3）对弱学习器，即 CART 回归树进行正则化剪枝

【sklearn 实现】

GBDT 回归算法

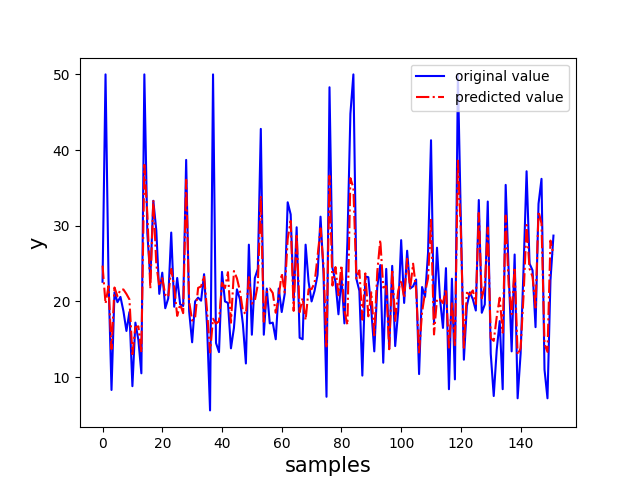
以 sklearn 中的波士顿房价数据集为例，选取其后两个特征来实现 GBDT 回归算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import r2_score

# 特征提取
def deal_data():
    boston = load_boston()  # sklearn的波士顿房价数据集
    df = pd.DataFrame(boston.data, columns=boston.feature_names)
    df['result'] = boston.target
    data = np.array(df)
    return data[:, :-1], data[:, -1]

# 模型训练
def train_model(features, labels):  
    # 建立GBDT回归模型
    model = GradientBoostingRegressor(n_estimators=300, learning_rate=0.005,
                                     max_depth=4, max_features='sqrt',
                                     min_samples_leaf=15, min_samples_split=10, 
                                     loss='ls')
    
    # 训练
    model.fit(features, labels)
    return model

# 模型评估
def estimate_model(y_true, y_pred):
    MSE = mean_squared_error(y_true, y_pred)
    RMSE = np.sqrt(MSE)
    MAE = mean_absolute_error(y_true, y_pred)
    R2 = r2_score(y_true, y_pred)
    indicators = {"MSE": MSE, "RMSE":RMSE, "MAE":MAE, "R2":R2}
    return indicators

# 可视化
def visualization(y_true, y_pred, model):
    # 绘图
    plt.plot(range(y_true.shape[0]), y_true, "b-") 
    plt.plot(range(y_true.shape[0]), y_pred, "r-.")
    plt.legend(["original value", "predicted value"])
    plt.xlabel("samples", fontsize="15")
    plt.ylabel("y", fontsize="15")
    
    plt.show()

if __name__ == "__main__":
    # 特征提取
    x, y = deal_data()
    
    # 简单交叉验证
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=0)
    
    # 模型训练
    model = train_model(x_train, y_train)
    
    # 预测结果
    y_pred = model.predict(x_test) # predict()输入输出均为二维
    print("y test:", y_test[:10]) # 测试集y值
    print("y pred:", y_pred[:10]) # 预测y值
    
    # 模型评估
    indicators = estimate_model(y_test, y_pred)
    print("MSE:", indicators["MSE"])
    print("RMSE:", indicators["RMSE"])
    print("MAE:", indicators["MAE"])
    print("R2:", indicators["R2"])
    
    # 可视化
    visualization(y_test, y_pred, model)

GBDT 分类算法

以 sklearn 中的鸢尾花数据集为例，选取其后两个特征来实现 AdaBoost 分类算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.metrics import confusion_matrix,accuracy_score,classification_report,precision_score,recall_score,f1_score
from matplotlib.colors import ListedColormap

# 特征提取
def deal_data():
    iris = load_iris()  # sklearn的鸢尾花数据集
    # iris分为三类，前50行一类，51-100行一类，101-150行一类
    X = iris.data[:, [2, 3]] # 选用后两个特征作为样本特征
    y = iris.target  #取species列，类别
    return X,y

# 数据归一化
def standard_scaler(X_train,X_test):
    sc = StandardScaler() # 初始化一个sc对象去对数据集作变换
    scaler = sc.fit(X_train) # 归一化，存有计算出的均值和方差
    X_train_std = scaler.transform(X_train) # 利用 scaler 进行标准化
    X_test_std = scaler.transform(X_test) # 利用 scaler 进行标准化
    return X_train_std, X_test_std

# 模型训练
def train_model(X_train_std, y_train):
    # 建立 GBDT 分类模型
    model = GradientBoostingClassifier(n_estimators=200, learning_rate=0.8,
                                      max_depth=4, max_features='sqrt',
                                      min_samples_leaf=15, min_samples_split=10)
    # 训练
    model.fit(X_train_std, y_train)
    return model

# 模型评估
def estimate_model(y_pred, y_test, model):
    # 混淆矩阵，三分类情况下，大小为 3*3
    cm2 = confusion_matrix(y_test,y_pred) 
    # 准确率
    acc = accuracy_score(y_test,y_pred)
    # 正确分类的样本数
    acc_num = accuracy_score(y_test,y_pred,normalize=False)
    # macro 分类报告
    macro_class_report = classification_report(y_test, y_pred,target_names=["类0","类1","类2"])
    # 微精确率
    micro_p = precision_score(y_test,y_pred,average='micro') 
    # 微召回率
    micro_r = recall_score(y_test,y_pred,average='micro')
    # 微F1得分
    micro_f1 = f1_score(y_test,y_pred,average='micro') 
    
    indicators = {"cm2":cm2,"acc":acc,"acc_num":acc_num,"macro_class_report":macro_class_report,"micro_p":micro_p,"micro_r":micro_r,"micro_f1":micro_f1}
    return indicators

# 可视化
def visualization(X, y, classifier, test_id=None, resolution=0.02):
    # 创建 color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    
    # 绘制决策边界
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1 #第一个特征取值范围作为横轴
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1 #第二个特征取值范围作为纵轴
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution)) # reolution为网格剖分粒度
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T) # 对组合的特征进行预测，ravel为数组展平
    Z = Z.reshape(xx1.shape) # Z是列向量
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap) # x和y为两个等长一维数组，z为二维数组，指定每一对xy所对应的z值
    plt.xlim(xx1.min(), xx1.max()) #对等高线间的区域进行填充
    plt.ylim(xx2.min(), xx2.max()) #对等高线间的区域进行填充
    
    # 全数据集，不同类别样本点的特征作为坐标(x,y)，用不同颜色画散点图
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl) 
        
    # 高亮测试集
    if test_id:
        X_test, y_test = X[test_id, :], y[test_id]
        # c设置颜色，测试集不同类别的实例点画图不区别颜色
        plt.scatter(x=X_test[:, 0], y=X_test[:, 1], alpha=1.0, c='gray', marker='^', linewidths=1, s=55, label='test set')
        
    plt.xlabel('petal length [standardized]')
    plt.ylabel('petal width [standardized]')
    plt.legend(loc='upper left')
    plt.tight_layout()
    plt.show()
    
if __name__ == "__main__":
    # 特征提取
    X, y = deal_data()
    
    # 简单交叉验证
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
    
    # 数据标准化
    X_train_std, X_test_std = standard_scaler(X_train, X_test)
    
    # 模型训练
    model = train_model(X_train_std, y_train)
    
    # 预测结果
    y_pred = model.predict(X_test_std)
    print("y test:", y_test) # 测试集y值
    print("y pred:", y_pred) # 预测y值
    
    # 模型评估
    indicators = estimate_model(y_pred, y_test, model)
    cm2 = indicators["cm2"] 
    print("混淆矩阵：\n", cm2) 
    acc =  indicators["acc"]
    print("准确率：", acc)
    acc_num =  indicators["acc_num"]
    print("正确分类的样本数：", acc_num)
    macro_class_report = indicators["macro_class_report"]
    print("macro 分类报告：\n", macro_class_report)
    micro_p = indicators["micro_p"]
    print("微精确率：", micro_p)
    micro_r = indicators["micro_r"]
    print("微召回率：", micro_r)
    micro_f1 = indicators["micro_f1"]
    print("微F1得分：", micro_f1)
    
    # 可视化
    X_combined_std = np.vstack((X_train_std, X_test_std))
    y_combined = np.hstack((y_train, y_test))
    # classifier为分类器，test_id为测试集序号
    visualization(X_combined_std, y_combined, classifier=model, test_id=range(105, 150))
感谢您对我的支持，让我继续努力分享有用的技术与知识点！