Reference
【概述】
在 朴素贝叶斯 中介绍了朴素贝叶斯分类器与其所假设的条件独立性,但该假设过于强势,在实际模型中有时并不满足,即样本的很多特征可能存在关联关系,并不独立
为解决上述问题,在朴素贝叶斯的基础上引入了限制条件:允许某些特征间存在依赖关系,即半朴素贝叶斯(Semi-naive Bayes)
半朴素贝叶斯适当地考虑一部分特征间的相互依赖信息,这样既不需要进行完全联合概率计算,又不至于彻底忽略了较强的属性依赖关系
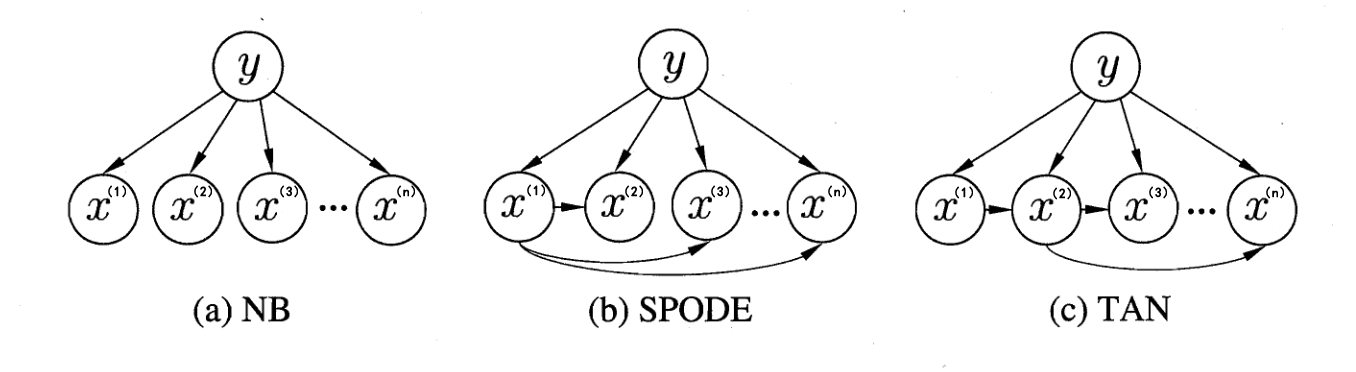
如下图,显示了朴素贝叶斯和两种半朴素贝叶斯分类器所考虑的特征依赖关系
【ODE 策略】
独依赖估计(One-dependent Estimator,ODE)是半朴素贝叶斯中最常用的策略,即假设每个特征在类别之外最多依赖一个其他特征,即:
其中,$a^{(j)}$ 为特征 $x^{(j)}$ 的父特征,即 $x^{(j)}$ 所依赖的特征
此时,对于每个特征 $x^{(j)}$,可以采用贝叶斯估计的方法来估计 $P(X^{(j)}=x^{(j)}|Y=c_k,a^{(j)})$ 的概率
于是,问题的关键就转化为如何确定每个特征的父特征,由此产生了不同的独依赖分类模型
【独依赖分类模型】
SPODE 模型
超父独依赖估计(Super-parent One-dependent Estimator,SPODE)模型,是最简单的 ODE 策略的实现
SPODE 假设所有特征都依赖于同一个特征,这个特征被称为超父(Super Parent),之后通过交叉验证的方法来确定超父特征
在确定超父特征 $X^{(f)}$ 后,概率公式变为:
在下图 SPODE 模型的特征依赖关系中,$x^{(1)}$ 即为超父特征

AODE 模型
平均独依赖估计(Averaged One-Dependent Estimator,AODE)模型是一种基于集成学习机制的独依赖分类器
与 SPODE 通过模型选择超父特征不同,其通过将每个特征分别作为超父来构建 SPODE,然后将有足够训练数据支撑的 SPODE 集成后作为最终结果,即:
其中,$N_{x^{(i)}}$ 为第 $i$ 个特征上取值为 $x^{(i)}$ 的样本数量,$\alpha’$ 为阈值参数
显然,AODE 需要估计 $P(Y=c_k,X^{(i)}=x^{(i)})$ 与 $P(X^{(j)}=x^{(j)}|Y=c_k,X^{(j)}=x^{(i)})$,计算公式如下:
其中,各参数含义如下:
- $N_{c_k}^{x^{(i)}}$:第 $i$ 个特征 $X^{(i)}$ 取值为 $x^{(i)}$ 且属于类别 $c_k$ 的样本个数
- $N_{c_k}^{x^{(i)},x^{(j)}}$:第 $i$ 个特征 $X^{(i)}$ 和第 $j$ 个特征 $X^{(j)}$ 分别取值 $x^{(i)}$ 和 $x^{(j)}$ 且类别为 $c_k$ 的样本个数
- $N^{(i)}$:第 $i$ 个特征可能的取值数
- $N^{(j)}$:第 $j$ 个特征可能的取值数
- $n$:样本个数
- $K$:类别取值个数
TAN 模型
树扩展朴素贝叶斯(Tree Augmented Naive Bayes,TAN)与 SPODE 模型类似,也是假设每个特征只依赖于一个特征,但与 SPODE 不同的是,其并不是统一的依赖于一个超父
其将 $m$ 个特征视为 $m$ 个结点,对于任意两个结点建立无向边,以构建一个无向完全图,同时,每条边的权重设为两条边的条件互信息(Conditional Mutual Information):
观察上式可知,其刻画了特征 $x^{(i)}$ 和 $x^{(j)}$ 在已知类别 $c_k$ 的情况下的相关性,即:
- 若 $P(x^{(i)},x^{(j)},c_k)=P(x^{(i)},c_k)P(x^{(j)},c_k)$,则 $I(x^{(i)};x^{(j)}|y)=0$,此时 $x^{(i)}$ 与 $x^{(j)}$ 无关
- 若 $P(x^{(i)},x^{(j)},c_k) > P(x^{(i)},c_k)P(x^{(j)},c_k)$,则 $I(x^{(i)};x^{(j)}|y)>0$,此时 $x^{(i)}$ 与 $x^{(j)}$ 正相关
- 若 $P(x^{(i)},x^{(j)},c_k) < P(x^{(i)},c_k)P(x^{(j)},c_k)$,则 $I(x^{(i)};x^{(j)}|y)<0$,此时 $x^{(i)}$ 与 $x^{(j)}$ 负相关
之后,对于建立好的无向完全图,根据最大带权生成树(Maximum Weighted Spanning Tree)算法,挑选根结点,同时根据特征 $x^{(i)}$ 和 $x^{(j)}$ 的相关性,将无向边设为有向边
最后,加入类别结点 $y$,增加类别结点 $y$ 到每个特征的有向边
这样一来,即可像 AODE 模型中一样计算概率,只是每个特征有着自己独特的父类