朴素贝叶斯

Reference

• 【辨析】先验概率、后验概率、似然概率
• 带你理解朴素贝叶斯分类算法
• 算法杂货铺——分类算法之朴素贝叶斯分类(Naive Bayesian classification)
• 贝叶斯估计
• 平滑处理—拉普拉斯（Laplace Smoothing）
• Naive Bayes classifier
• Additive smoothing

【概述】

贝叶斯分类模型是基于贝叶斯定理与特征条件独立假设的分类模型，朴素贝叶斯（Naive Bayes）是贝叶斯分类模型中最简单、最常见的一种分类方法，该方法从概率论的角度来进行分类预测，实现简单，预测效率高

贝叶斯定理、贝叶斯分类模型、朴素贝叶斯三者关系如下：

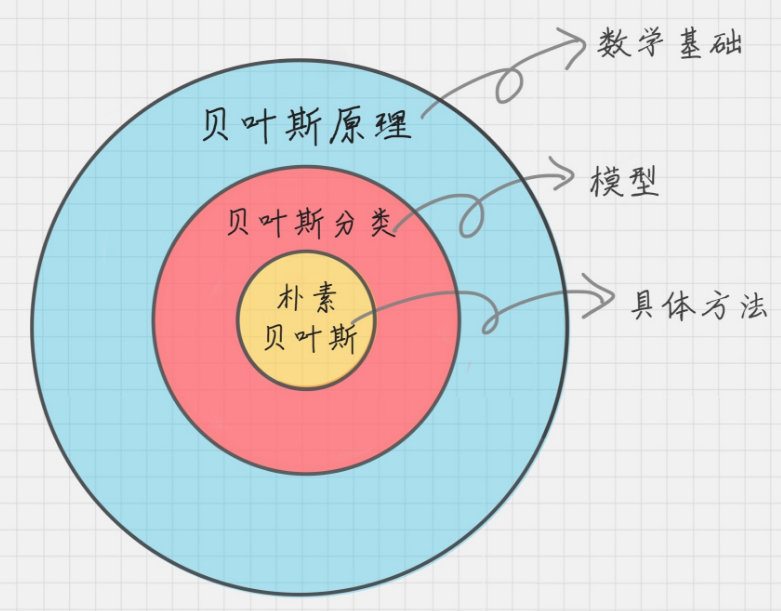
之所以叫做朴素贝叶斯，一方面是其基于贝叶斯定理，另一方面，朴素是指其基于特征独立性假设，各特征不会相互影响，大大减少了计算概率的难度

该方法的基本思想是：对于给定的训练集，当要根据多个特征对数据进行分类时，通常假设这些特征相互独立，然后利用条件概率乘法法则得到每一个分类的概率，对于给定的输入样本 $\mathbf{x}$，利用模型求出后验概率最大的作为预测输出 $y$

【贝叶斯公式】

假设事件 $A$ 发生的概率为 $P(A)$，事件 $B$ 发生的概率为 $P(B)$，在事件 $B$ 发生的情况下，事件 $A$ 发生的概率为 $P(A|B)$，则事件 $A$ 发生的情况下事件 $B$ 发生的概率为：

$$\begin{align*} P(B|A) &= \frac{P(AB)}{P(A)} \\ &= \frac{P(A|B)P(B)}{P(A)} \end{align*}$$

其中，$P(B|A)$ 称为后验概率（Posterior Probability），$P(A)$、$P(B)$ 称为先验概率（Prior Probability），$P(A|B)$ 称为似然概率（Likelihood）

对于分类算法来说，令数据特征为事件 $A$，令类别为事件 $B$，则此时贝叶斯公式可表达为如下形式：

$$P(类别|特征)=\frac{P(特征|类别)P(类别)}{P(特征)}$$

为便于表述，记数据特征为 $\mathbb{x}$，记类别为 $c$，那么有：

$$P(c|\mathbb{x}) = \frac{P(\mathbb{x}|c) P(c)}{P(\mathbb{x})}$$

进一步，对于先验概率 $P(c)$ 和 $P(\mathbb{x})$，表示类别的先验概率 $P(类别)$ 称为类先验概率（Class Prior Probability），表示做出预测的先验概率 $P(特征)$ 称为预测先验概率（Predictor Prior Probability）

【朴素贝叶斯模型】

设输入空间 $\mathcal{X}\subseteq \mathbb{R}^m $ 为 $m$ 维向量的集合，输出空间为类标记集合 $\mathcal{Y}=\{c_1,c_2,…,c_K\}$，输入为特征向量 $\mathbf{x}\in \mathcal{X}$，输出为类标记 $y\in \mathcal{Y}$，$X$ 是定义在输入空间 $\mathcal{X}$ 上的随机向量，$Y$ 是定义在输出空间 $\mathcal{Y}$ 上的随机变量，$P(X,Y)$ 是 $X$ 和 $Y$ 的联合概率分布

已知给定的训练集 $T=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),…,(\mathbf{x_n},y_n)\}$ 由 $P(X,Y)$ 独立同分布产生，对于第 $i$ 组样本对，输入 $\mathbf{x_i}$ 具有 $m$ 个特征值，即：$\mathbf{x_i} =(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{X} \subseteq \mathbb{R}^m$，输出 $y_i\in\mathcal{Y}= \{c_1,c_2,…,c_K\}$ 为实例的类别

根据训练集 $T$ 可知，类标记的先验概率分布为：

$$P(Y=c_k),\quad k=1,2,...,K$$

亦可知在训练集 $T$ 上输入 $\mathbf{x}_i$ 的条件概率分布为：

$$P(X=\mathbf{x}_i|Y=c_k) = P(X^{(1)}=x_i^{(1)},...,X^{(m)}=x_i^{(m)}|Y=c_k),\quad k=1,2,...,K$$

对于 $P(X=\mathbf{x}_i|Y=c_k)$，假设 $\mathbf{x}$ 的各分量 $x_i^{(j)}$ 可取值的个数为 $S_j,j=1,2,…,m$，又由于 $Y$ 可取值个数为 $K$，那么参数的个数为：

$$K\prod _{j=1}^nS_j$$

可以发现，条件概率分布 $P(X=\mathbf{x_i}|Y=c_k)$ 有着指数级的参数，对其进行参数估计是不可行的，为此，作条件独立性假设

也就是说，假设用于分类的特征在类确定的条件下都是独立的，此时，在训练集 $T$ 上输入 $\mathbf{x}_i$ 的条件概率分布为：

$$\begin{align*} P(X=\mathbf{x}_i|Y=c_k) =& P(X^{(1)}=x^{(1)}_i,...,X^{(m)}=x^{(m)}_i|Y=c_k) \\ =&\prod_{j=1}^m P(X^{(j)}=x^{(j)}|Y=c_k) \end{align*}$$

另一方面，根据全概率公式：

$$P(A)=\sum_{i=1}^nP(A|B_i)P(B_i)$$

在训练集 $T$ 上输入 $\mathbf{x}_i$ 的概率分布为：

$$P(X=\mathbb{x_i}) = \sum_{k=1}^K P(X=\mathbb{x}_i|Y=c_k)P(Y=c_k)$$

这样，根据朴素贝叶斯公式，当给定一个新的输入 $\mathbb{x}\in\mathbb{R}^m$ 时，即可计算出该输入所属类别 $c_k$ 的后验概率分布，即：

$$\begin{align*} P(Y=c_k|X=\mathbb{x}) &= \frac{P(X=\mathbb{x}|Y=c_k) P(Y=c_k)}{P(X=\mathbb{x})} \\ &= \frac{P(Y=c_k) \prod\limits_{j=1}^m P(X^{(j)}=x^{(j)}|Y=c_k)}{\sum\limits_{k'=1}^K \Big[ P(X=\mathbb{x}|Y=c_{k'}) P(Y=c_{k'})\Big]} \\ &= \frac{P(Y=c_k) \prod\limits_{j=1}^m P(X^{(j)}=x^{(j)}|Y=c_k)}{\sum\limits_{k'=1}^K \Bigg[ P(Y=c_{k'}) \prod\limits_{j=1}^m P(X^{(j)}=x^{(j)}|Y=c_{k'}) \Bigg] } \end{align*}$$

由此，对于给定新的输入 $\mathbb{x}\in\mathbb{R}^m$，朴素贝叶斯分类器即可表示为：

$$y=\arg\max_{c_k} \frac{P(Y=c_k) \prod\limits_{j=1}^m P(X^{(j)}=x^{(j)}|Y=c_k)}{\sum\limits_{k'=1}^K \Bigg[ P(Y=c_{k'}) \prod\limits_{j=1}^m P(X^{(j)}=x^{(j)}|Y=c_{k'}) \Bigg] }$$

可以注意到，上式中，分母对所有的 $c_k$ 都是相同的，将分母忽略，即有：

$$\hat{y}=\arg\max_{c_k} P(Y=c_k) \prod\limits_{j=1}^m P(X^{(j)}=x^{(j)}|Y=c_k)$$

此时，模型学习意味着估计类先验概率 $P(Y=c_k)$ 与似然概率 $P(X^{(j)}=x^{(j)}|Y=c_k)$

【期望风险最小化与后验概率最大化】

对于分类决策函数 $\hat{y}=f(\mathbf{x})$，假设使用 0-1 损失函数：

$$L(y,f(x))= \left\{\begin{array}{rl} 1, & y \neq f(x)\\ 0, & y = f(x) \end{array}\right.$$

对于联合分布 $P(X,Y)$，取条件期望，此时期望风险函数为：

$$\begin{align*} R_{exp}(f) &= E[L(Y,f(X))] \\ &= E_X\sum_{k=1}^KL(c_k,f(X))P(c_k|X) \end{align*}$$

为使期望风险最小化，只需对 $X=\mathbb{x}$ 逐个极小化，有：

$$\begin{align*} \hat{y} &= \arg \min_{y\in\mathcal{Y}}\sum_{k=1}^K L(c_k,y)P(c_k|X=\mathbb{x}) \\ &= \arg \min_{y\in\mathcal{Y}}\sum_{k=1}^K P(y\neq c_k|X=\mathbb{x}) \\ &= \arg \min_{y\in\mathcal{Y}}[1-P(y=c_k|X=\mathbb{x})] \\ &= \arg \max_{y\in\mathcal{Y}}P(y=c_k|X=\mathbb{x}) \end{align*}$$

可以发现，在朴素贝叶斯中，期望风险最小化与后验概率最大化是等价的