Alex_McAvoy

想要成为渔夫的猎手

朴素贝叶斯参数估计

发表于 分类于 ， ，
本文字数： 13k 阅读时长 ≈ 12 分钟

Reference

【朴素贝叶斯参数估计】

对于朴素贝叶斯分类器：

模型学习意味着对类先验概率 $P(Y=c_k)$ 与似然概率 $P(X^{(j)}=x^{(j)}|Y=c_k)$ 进行参数估计，此时，可以使用极大似然估计来进行参数估计

由于离散型随机变量是直接将频率当做概率，因此若一个属性未出现时，计算得出的概率为 $0$

为避免这种错误，可以使用贝叶斯估计，通过引入 $\lambda=1$ 进行拉普拉斯平滑修正，即假设特征值和类别的均匀分布，但当样本数目足够大时，该影响会被消除

【极大似然估计】

朴素贝叶斯的学习就意味着对类先验概率 $P(Y=c_k)$ 与似然概率 $P(X^{(j)}=x^{(j)}|Y=c_k)$ 进行参数估计

对于类先验概率 $P(Y=c_k)$，可以通过对训练集进行经验统计而得出，对于样本容量为 $n$ 的训练集，有：

对于似然概率 $P(X^{(j)}=x^{(j)}|Y=c_k)$，根据贝叶斯公式，可写为：

对于分子，根据条件概率公式，有：

假设第 $j$ 个特征 $x^{(j)}$ 可能取值的集合为 $\{a^{(j)}_1,a^{(j)}_2,…,a^{(j)}_{S_j}\}$，其中，$a^{(j)}_l$ 代表第 $j$ 个特征可能取的第 $l$ 个值，$S_j$ 代表第 $j$ 个特征可取值的数量，那么有：

其中，$j=1,2,…,n$，$l=1,2,…,S_j$，$k=1,2,…,K$

于是，似然概率为：

即：

其中，$j=1,2,…,n$，$l=1,2,…,S_j$，$k=1,2,…,K$

【贝叶斯估计】

与极大似然估计相似，对于贝叶斯估计，设 $\lambda\geq0$，则对于类先验概率 $P(Y=c_k)$，有：

进一步，假设第 $j$ 个特征 $x^{(j)}$ 可能取值的集合为 $\{a^{(j)}_1,a^{(j)}_2,…,a^{(j)}_{S_j}\}$，其中，$a^{(j)}_l$ 代表第 $j$ 个特征可能取的第 $l$ 个值，$S_j$ 代表第 $j$ 个特征可取值的数量，那么有：

其中，$j=1,2,…,n$，$l=1,2,…,S_j$，$k=1,2,…,K$

可以发现，贝叶斯估计等价于在随机变量各个取值的频数上赋予一个正数 $\lambda\geq0$，而当 $\lambda=0$ 时，即为极大似然估计

一般来说，常取 $\lambda=1$，此时称为拉普拉斯平滑（Laplace smoothing）

那么，对于任意的 $l$ 和 $k$，有：

【实例】

问题描述

现给出一个身高为 高，体重为 中，鞋码为 中 的数据，根据下图中的数据，判断这个数据是男是女

问题分析

设特征：身高为 高 为 $A_1$，体重为 中 为 $A_2$，鞋码为 中 为 $A_3$，类别：男 $C_1$，女 $C_2$

首先要求在 $A_1,A_2,A_3$ 下 $C_k$ 的概率，即：

由于类别仅有两种，因此仅需计算 $P(C_1|A_1A_2A_3)$ 和 $P(C_2|A_1A_2A_3)$，然后输出较大的概率所对应的分类

根据朴素贝叶斯模型：

这就等价于求 $P(A_1A_2A_3|C_k)P(C_k)$ 的最大值

极大似然估计

假设 $A_i$ 之间是相互独立的，那么有：

对于先验概率 $P(Y=c_k)$，其极大似然估计为：

根据数据集，可得：

对于似然概率 $P(X^{(j)}=a_{jl}|Y=c_k)$ ，其极大似然估计为：

根据数据集，可得：

因此，由朴素贝叶斯模型：

可得：

综上，对于给定身高为 高，体重为 中，鞋码为 中 的数据，应是 $C_1$ 类别，为男性

贝叶斯估计

假设 $A_i$ 之间是相互独立的，那么有：

对于先验概率 $P(Y=c_k)$，其贝叶斯估计为：

根据数据集，可得：

对于似然概率 $P(X^{(j)}=a^{(j)}_l|Y=c_k)$ ，其贝叶斯估计为：

根据数据集，可得：

因此，由朴素贝叶斯模型：

可得：

综上，对于给定身高为 高，体重为 中，鞋码为 中 的数据，应是 $C_1$ 类别，为男性

【sklearn 实现】

概述

sklearn 中提供了若干朴素贝叶斯的实现算法，对于不同的朴素贝叶斯实现，主要是对 $P(X^{(j)}=x^{(j)}|Y=c_k)$ 的分布假设不同，以采用不同的参数估计方式

对于朴素贝叶斯来说，其主要就是计算似然概率 $P(X^{(j)}=x^{(j)}|Y=c_k)$，一旦似然概率确定，最终所属每个类别的概率自然也就轻易得出

常用的两种朴素贝叶斯为：

  • 高斯朴素贝叶斯：GaussianNB()
  • 伯努利朴素贝叶斯：BernoulliNB()

高斯朴素贝叶斯

高斯朴素贝叶斯适用于连续型随机变量，其假设各特征 $x^{(j)}$ 在各类别 $c_k$ 下服从正态分布，因此算法内部使用正态分布的概率密度函数来计算概率，即：

其中，参数含义如下：

  • $\mu_{c_k}$：在类别 $c_k$ 的样本中，特征 $x^{(j)}$ 的均值
  • $\sigma_{c_k}$：在类别 $c_k$ 的样本中，特征 $x^{(j)}$ 的标准差

以 sklearn 中的鸢尾花数据集为例，选取其后两个特征来实现高斯朴素贝叶斯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
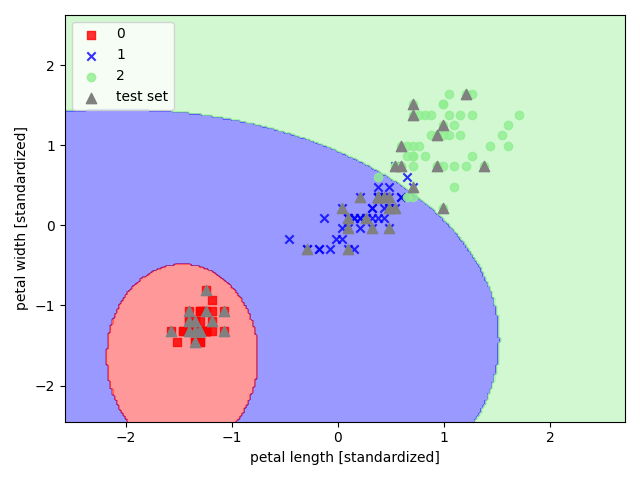
127
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import confusion_matrix,accuracy_score,classification_report,precision_score,recall_score,f1_score
from matplotlib.colors import ListedColormap

# 特征提取
def deal_data():
    iris = load_iris()  # sklearn的鸢尾花数据集
    # iris分为三类，前50行一类，51-100行一类，101-150行一类
    X = iris.data[:, [2, 3]] # 选用后两个特征作为样本特征
    y = iris.target  #取species列，类别
    return X,y

# 数据归一化
def standard_scaler(X_train, X_test):
    sc = StandardScaler() # 初始化一个sc对象去对数据集作变换
    scaler = sc.fit(X_train) # 归一化，存有计算出的均值和方差
    X_train_std = scaler.transform(X_train) # 利用 scaler 进行标准化
    X_test_std = scaler.transform(X_test) # 利用 scaler 进行标准化
    return X_train_std, X_test_std

# 模型训练
def train_model(X_train_std, y_train):
    # 建立高斯朴素贝叶斯模型
    model = GaussianNB()
    # 训练
    model.fit(X_train_std, y_train)
    return model

# 模型评估
def estimate_model(y_pred, y_test, model):
    # 混淆矩阵，三分类情况下，大小为 3*3
    cm2 = confusion_matrix(y_test,y_pred) 
    # 准确率
    acc = accuracy_score(y_test,y_pred)
    # 正确分类的样本数
    acc_num = accuracy_score(y_test,y_pred,normalize=False)
    # macro 分类报告
    macro_class_report = classification_report(y_test, y_pred,target_names=["类0","类1","类2"])
    # 微精确率
    micro_p = precision_score(y_test,y_pred,average='micro') 
    # 微召回率
    micro_r = recall_score(y_test,y_pred,average='micro')
    # 微F1得分
    micro_f1 = f1_score(y_test,y_pred,average='micro') 
    
    indicators = {"cm2":cm2,"acc":acc,"acc_num":acc_num,"macro_class_report":macro_class_report,"micro_p":micro_p,"micro_r":micro_r,"micro_f1":micro_f1}
    return indicators

# 可视化
def visualization(X, y, classifier, test_id=None, resolution=0.02):
    # 创建 color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    
    # 绘制决策边界
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1 #第一个特征取值范围作为横轴
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1 #第二个特征取值范围作为纵轴
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution)) # reolution为网格剖分粒度
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T) # 对组合的特征进行预测，ravel为数组展平
    Z = Z.reshape(xx1.shape) # Z是列向量
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap) # x和y为两个等长一维数组，z为二维数组，指定每一对xy所对应的z值
    plt.xlim(xx1.min(), xx1.max()) #对等高线间的区域进行填充
    plt.ylim(xx2.min(), xx2.max()) #对等高线间的区域进行填充
    
    # 全数据集，不同类别样本点的特征作为坐标(x,y)，用不同颜色画散点图
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl) 
        
    # 高亮测试集
    if test_id:
        X_test, y_test = X[test_id, :], y[test_id]
        # c设置颜色，测试集不同类别的实例点画图不区别颜色
        plt.scatter(x=X_test[:, 0], y=X_test[:, 1], alpha=1.0, c='gray', marker='^', linewidths=1, s=55, label='test set')
        
    plt.xlabel('petal length [standardized]')
    plt.ylabel('petal width [standardized]')
    plt.legend(loc='upper left')
    plt.tight_layout()
    plt.show()
    
if __name__ == "__main__":
    # 特征提取
    X, y = deal_data()
    
    # 简单交叉验证
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
    
    # 数据标准化
    X_train_std, X_test_std = standard_scaler(X_train, X_test)
    
    # 模型训练
    model = train_model(X_train_std, y_train)
    
    # 预测结果
    y_pred = model.predict(X_test_std)
    print("y test:", y_test) # 测试集y值
    print("y pred:", y_pred) # 预测y值
    
    # 模型评估
    indicators = estimate_model(y_pred, y_test, model)
    cm2 = indicators["cm2"] 
    print("混淆矩阵：\n", cm2) 
    acc =  indicators["acc"]
    print("准确率：", acc)
    acc_num =  indicators["acc_num"]
    print("正确分类的样本数：", acc_num)
    macro_class_report = indicators["macro_class_report"]
    print("macro 分类报告：\n", macro_class_report)
    micro_p = indicators["micro_p"]
    print("微精确率：", micro_p)
    micro_r = indicators["micro_r"]
    print("微召回率：", micro_r)
    micro_f1 = indicators["micro_f1"]
    print("微F1得分：", micro_f1)
    
    # 可视化
    X_combined_std = np.vstack((X_train_std, X_test_std))
    y_combined = np.hstack((y_train, y_test))
    # classifier为分类器，test_id为测试集序号
    visualization(X_combined_std, y_combined, classifier=model, test_id=range(105, 150))

伯努利朴素贝叶斯

伯努利朴素贝叶斯适用于离散型随机变量，其假设各特征 $x^{(j)}$ 在各类别 $c_k$ 下服从 n 重伯努利分布，因此算法内部会首先对特征值 $x^{(j)}$ 进行二值化处理，之后依照如下公式进行概率计算：

在训练集中，会进行如下估计：

其中，参数含义如下：

  • $N_{c_k}^{(j)}$：第 $j$ 个特征中属于类别 $c_k$，且特征值为 $1$ 的样本个数
  • $N_{c_k}$：属于类别 $c_k$ 的样本个数
  • $\alpha$：平滑系数

以 sklearn 中的鸢尾花数据集为例，选取其后两个特征来实现伯努利朴素贝叶斯

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
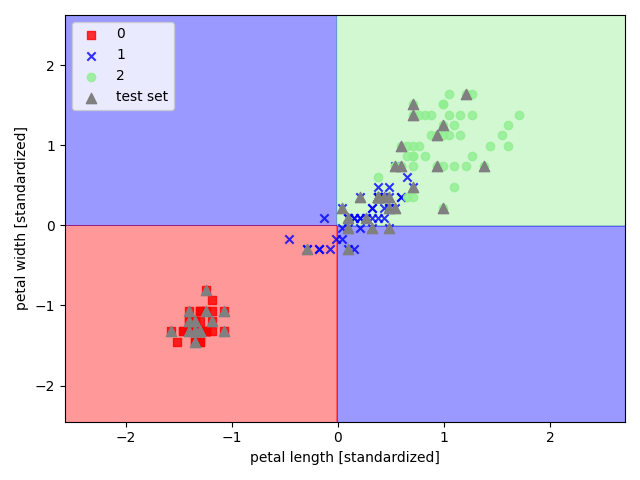
127
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
from sklearn.naive_bayes import BernoulliNB
from sklearn.metrics import confusion_matrix,accuracy_score,classification_report,precision_score,recall_score,f1_score
from matplotlib.colors import ListedColormap

# 特征提取
def deal_data():
    iris = load_iris()  # sklearn的鸢尾花数据集
    # iris分为三类，前50行一类，51-100行一类，101-150行一类
    X = iris.data[:, [2, 3]] # 选用后两个特征作为样本特征
    y = iris.target  #取species列，类别
    return X,y

# 数据归一化
def standard_scaler(X_train, X_test):
    sc = MinMaxScaler() # 初始化一个sc对象去对数据集作变换
    scaler = sc.fit(X_train) # 归一化，存有计算出的均值和方差
    X_train_std = scaler.transform(X_train) # 利用 scaler 进行标准化
    X_test_std = scaler.transform(X_test) # 利用 scaler 进行标准化
    return X_train_std, X_test_std

# 模型训练
def train_model(X_train_std, y_train):
    # 建立伯努利朴素贝叶斯模型
    model = BernoulliNB(alpha=0.15, binarize=0.5)
    # 训练
    model.fit(X_train_std, y_train)
    return model

# 模型评估
def estimate_model(y_pred, y_test, model):
    # 混淆矩阵，三分类情况下，大小为 3*3
    cm2 = confusion_matrix(y_test,y_pred) 
    # 准确率
    acc = accuracy_score(y_test,y_pred)
    # 正确分类的样本数
    acc_num = accuracy_score(y_test,y_pred,normalize=False)
    # macro 分类报告
    macro_class_report = classification_report(y_test, y_pred,target_names=["类0","类1","类2"])
    # 微精确率
    micro_p = precision_score(y_test,y_pred,average='micro') 
    # 微召回率
    micro_r = recall_score(y_test,y_pred,average='micro')
    # 微F1得分
    micro_f1 = f1_score(y_test,y_pred,average='micro') 
    
    indicators = {"cm2":cm2,"acc":acc,"acc_num":acc_num,"macro_class_report":macro_class_report,"micro_p":micro_p,"micro_r":micro_r,"micro_f1":micro_f1}
    return indicators

# 可视化
def visualization(X, y, classifier, test_id=None, resolution=0.02):
    # 创建 color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    
    # 绘制决策边界
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1 #第一个特征取值范围作为横轴
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1 #第二个特征取值范围作为纵轴
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(x2_min, x2_max, resolution)) # reolution为网格剖分粒度
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T) # 对组合的特征进行预测，ravel为数组展平
    Z = Z.reshape(xx1.shape) # Z是列向量
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap) # x和y为两个等长一维数组，z为二维数组，指定每一对xy所对应的z值
    plt.xlim(xx1.min(), xx1.max()) #对等高线间的区域进行填充
    plt.ylim(xx2.min(), xx2.max()) #对等高线间的区域进行填充
    
    # 全数据集，不同类别样本点的特征作为坐标(x,y)，用不同颜色画散点图
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl) 
        
    # 高亮测试集
    if test_id:
        X_test, y_test = X[test_id, :], y[test_id]
        # c设置颜色，测试集不同类别的实例点画图不区别颜色
        plt.scatter(x=X_test[:, 0], y=X_test[:, 1], alpha=1.0, c='gray', marker='^', linewidths=1, s=55, label='test set')
        
    plt.xlabel('petal length [standardized]')
    plt.ylabel('petal width [standardized]')
    plt.legend(loc='upper left')
    plt.tight_layout()
    plt.show()
    
if __name__ == "__main__":
    # 特征提取
    X, y = deal_data()
    
    # 简单交叉验证
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
    
    # 数据标准化
    X_train_std, X_test_std = standard_scaler(X_train, X_test)
    
    # 模型训练
    model = train_model(X_train_std, y_train)
    
    # 预测结果
    y_pred = model.predict(X_test_std)
    print("y test:", y_test) # 测试集y值
    print("y pred:", y_pred) # 预测y值
    
    # 模型评估
    indicators = estimate_model(y_pred, y_test, model)
    cm2 = indicators["cm2"] 
    print("混淆矩阵：\n", cm2) 
    acc =  indicators["acc"]
    print("准确率：", acc)
    acc_num =  indicators["acc_num"]
    print("正确分类的样本数：", acc_num)
    macro_class_report = indicators["macro_class_report"]
    print("macro 分类报告：\n", macro_class_report)
    micro_p = indicators["micro_p"]
    print("微精确率：", micro_p)
    micro_r = indicators["micro_r"]
    print("微召回率：", micro_r)
    micro_f1 = indicators["micro_f1"]
    print("微F1得分：", micro_f1)
    
    # 可视化
    X_combined_std = np.vstack((X_train_std, X_test_std))
    y_combined = np.hstack((y_train, y_test))
    # classifier为分类器，test_id为测试集序号
    visualization(X_combined_std, y_combined, classifier=model, test_id=range(105, 150))
感谢您对我的支持，让我继续努力分享有用的技术与知识点！