References:
【Cover 定理】
在实际应用中,分类问题有许多是线性不可分的
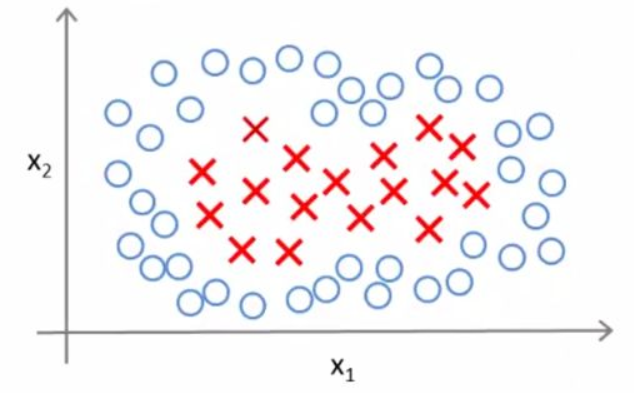
对于这样的线性不可分问题,可以通过多项式回归结合 Logistic 回归来得到想要的结果:
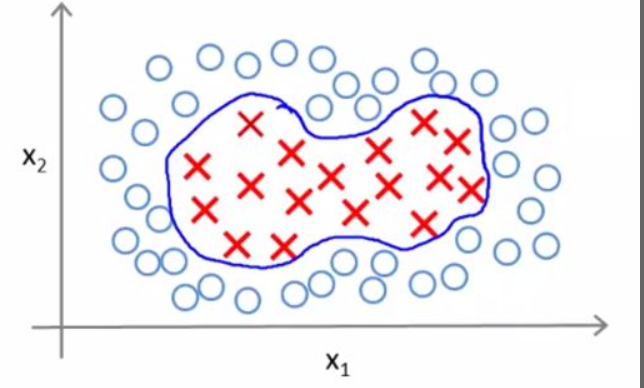
举例来说,对于如下图的一维数据:

无法使用一根直线将数据区分,因为不管怎么分,都会出现错误分类的情况:

如果原来的数据是 $X=[x]$ ,给它增加一个维度 $x^2$,数据就从一维变成二维 $X=[x,x^2]$,此时提升维度后的数据集已经变为线性可分了,可以用 $y=x$ 来将数据分开:
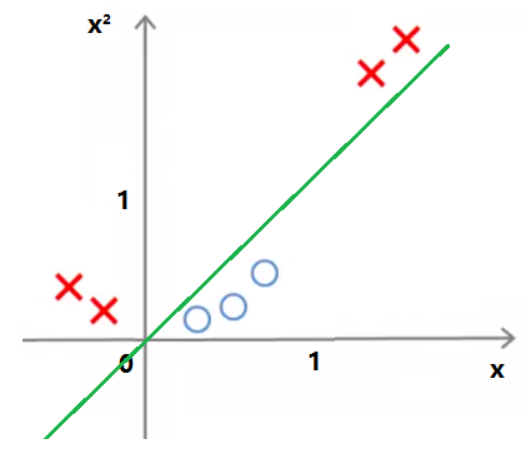
回到一维中,使用 Logistic 回归可以得到分界线方程:$\theta_1+\theta_2x+\theta_3x^2=0$,经过梯度下降优化后,可以得到曲线 $x^2-x=0$
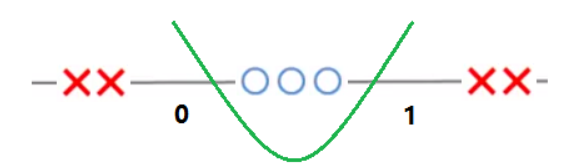
也就是说,多项式回归通过将数据从低维映射到高维,将原本线性不可分的情况变成了线性可分的情况
提升维度后,原本非线性的数据变成线性可分的数据,这在数学上是有严格证明的,即Cover 定理:当空间的维数 $D$ 越大时,在该空间的 $n$ 个数据点间的线性可分的概率就越大
需要的是,Cover 定理描述的是线性可分的概率,并非提供了提升维度就一定可以线性可分的依据
【特征构建】
根据 Cover 定理,在面对低维且线性不可分的数据时,可以将数据从低维空间映射到高维空间从而提升线性可分的概率
举例来说,对于向量 $\mathbf{x}=[1\quad x_1\quad x_2]$,使用多项式平方映射后,有:
在映射前的数据维度为 $3$,经过映射后提升成了 $9$,此时向量内的线性特征更加显著
这类将低维数据转变为高维的映射 $\phi(\mathbf{x})$ 被称为特征构建(Feature Build),映射后的向量被称为特征向量
使用多项式回归将数据从低维映射到高维,随着维度的增加,会导致计算量会以几何级数增加,为此,引入了核方法(Kernel Method),其是一种利用核函数(Kernel Function)将低维空间的非线性可分问题,转化为高维空间的线性可分问题的方法
【核函数】
设输入空间 $\mathcal{X}$ 是 $n$ 维欧氏空间 $\mathbb{R}^n$ 的子集或离散集合,特征空间 $\mathcal{H}$ 是希尔伯特空间,若存在一个从 $\mathcal{X}$ 到 $\mathcal{H}$ 的映射:
使得对所有的 $\mathbf{x},\mathbf{z}\in\mathcal{X}$ 满足:
则称 $K(\mathbf{x},\mathbf{z})$ 为核函数,$\phi(\cdot)$ 为映射函数,其中 $\phi(\mathbf{x})\cdot\phi(\mathbf{z})$ 为 $\phi(\mathbf{x})$ 和 $\phi(\mathbf{z})$ 的内积
需要注意的是,对于给定的核函数 $K(\mathbf{x},\mathbf{z})$,特征空间 $\mathcal{H}$ 和映射函数 $\phi(\cdot)$ 的取法不唯一,可以取不同的特征空间,在同一特征空间中也可以取不同的映射
【正定核】
已知映射函数 $\phi(\cdot)$,可以通过 $\phi(\mathbf{x})$ 和 $\phi(\mathbf{z})$ 的内积来求得核函数 $K(\mathbf{x},\mathbf{z})$,那么能否不构造映射 $\phi(\cdot)$ 就能直接判断一个给定的函数 $K(\mathbf{x},\mathbf{z})$ 是否为核函数?或者说,函数 $K(\mathbf{x},\mathbf{z})$ 满足什么样的条件,才能成为核函数?
再生核与再生核希尔伯特空间
定义映射:
根据这一映射,对任意 $\mathbf{x}_i\in \mathcal{X},\alpha_i\in\mathbb{R},i=1,2,\cdots,m$,定义线性组合:
考虑由上述线性组合为元素的集合 $S$,由于集合 $S$ 对加法和数乘运算是封闭的,因此 $S$ 构成一个向量空间
此时,对于向量空间上的任意线性组合 $f,g\in S$
在向量空间 $S$ 上定义内积运算:
此时,向量空间 $S$ 为一内积空间
进一步,根据内积运算,可导出范数:
故而内积空间 $S$ 是一个赋范向量空间
根据泛函分析理论,对于不完备的赋范向量空间 $S$,一定可以使其完备化,得到完备的赋范向量空间 $\mathcal{H}$,即希尔伯特空间(Hilbert Space)
而对于赋范向量空间 $S$,其完备化后得到的希尔伯特空间 $\mathcal{H}$,由于函数 $K(\cdot,\mathbf{x})$ 具备再生性,即:
故称函数 $K(\cdot,\mathbf{x})$ 为再生核(Reproducing Kernel),称希尔伯特空间 $\mathcal{H}$ 为再生核希尔伯特空间(Reproducing Kernel Hilbert Space)
事实上,任何一个核函数,都隐式地定义了一个再生核希尔伯特空间
正定核
设 $\mathcal{X}\subset \mathbb{R}^n$,$K(\mathbf{x},\mathbf{z})$ 是定义在 $\mathcal{X}\times\mathcal{X}$ 上的对称函数,若对 $\forall\mathbf{x}_i\in \mathcal{X},i=1,2,\cdots,m$,$K(\mathbf{x},\mathbf{z})$ 对应的 Gram 矩阵
是半正定矩阵,即对于任意非零实向量 $\mathbf{a}$,有:
则称 $K(\mathbf{x},\mathbf{z})$ 是正定核
对于 $K(\mathbf{x},\mathbf{z})$,可以构造其从 $\mathcal{X}$ 到某个希尔伯特空间 $\mathcal{H}$ 的映射:
根据函数 $K(\cdot,\mathbf{x})$ 的再生性,可得:
即正定核 $K(\mathbf{x},\mathbf{z})$ 是定义在 $\mathcal{X}\times\mathcal{X}$ 上的核函数
正定核在构造核函数是十分有用,但对于一个具体函数 $K(\mathbf{x},\mathbf{z})$ 来说,检验其是否为正定核函数并不容易,因为要求对任意有限输入集 $\{\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_m\}$ 需要验证 $K$ 对应的 Gram 矩阵是半正定的
因此,在实际应用中,常采用已有的核函数
【常用核函数】
常用的核函数如下:
- 线性核函数: $K(\mathbf{x},\mathbf{z})=\mathbf{x}\cdot\mathbf{z}$
- 多项式核函数:$K(\mathbf{x},\mathbf{z})=(\mathbf{x}\cdot\mathbf{z}+1)^p$,其中 $p\geq 1$ 为多项式的次数
- 高斯(径向基)核函数:$K(\mathbf{x},\mathbf{z})=\exp(-\frac{1}{2\sigma}||\mathbf{x}-\mathbf{z}||^2_2)$,其中 $\sigma>0$ 为带宽
- 拉普拉斯核函数:$K(\mathbf{x},\mathbf{z})=\exp(-\frac{1}{\sigma}||\mathbf{x}-\mathbf{z}||_2)$,其中 $\sigma>0$ 为带宽
- Sigmoid 核函数:$K(\mathbf{x},\mathbf{z})=\text{sigmoid}(\beta\mathbf{x}\cdot\mathbf{z}+\theta)$,其中 $\beta>0,\theta<0$
【表示定理】
设 $\mathcal{H}$ 为核函数 $K(\mathbf{x},\mathbf{z})$ 对应的再生核希尔伯特空间,$||h||_{\mathcal{H}}$ 为再生核希尔伯特空间中关于 $h$ 的范数,对任意单调递增函数 $f(x)$ 和任意非负损失函数 $L(\mathbf{x})$,对于优化问题:
的解可以写为:
上述定理即为表示定理(Representer Theorem),其说明了在高维甚至无限维的正则化泛函可以由数据样本张成的有限维空间表示,这避免了直接在高维空间进行优化
表示定理对损失函数没有任何限制,只要求正则化项 $f(x)$ 单调递增,甚至不要求 $f(x)$ 是凸函数
也就是说,对于一般的损失函数和正则化项,优化问题 $F(h)$ 的最优解 $h^*(\mathbf{x})$ 都可以表示为核函数 $K(\mathbf{x},\mathbf{z})$ 的线性组合
由此,发展出一系列的基于核函数的核方法,即通过引入核函数进行核化,将线性学习模型扩展为非线性学习模型,常见的有非线性支持向量机、核主成分分析、核线性判别分析等

