Alex_McAvoy

想要成为渔夫的猎手

二元 Logistic 回归

发表于 分类于 ， ，
本文字数： 13k 阅读时长 ≈ 12 分钟

Reference

【概述】

对数几率回归（Logistic regression）即 Logistic 回归，虽然名为回归，但其实际上是一种解决分类问题的分类学习方法，在现实中应用十分广泛，比如垃圾邮件识别，手写数字识别，人脸识别，语音识别等

对于分类问题来说，如果利用线性回归来拟合，假设函数 $f(\mathbf{x_i};\boldsymbol{\theta})$ 的输出值会出现 $f(\mathbf{x_i};\boldsymbol{\theta})>1$ 或 $f(\mathbf{x_i};\boldsymbol{\theta})<0$ 的情况，无法对结果进行归纳，因此，有了 Logistic 回归

其利用一个单调可微的激活函数，将分类任务的真实标记 $y_i$ 与线性回归模型的预测值 $f(\mathbf{x_i};\boldsymbol{\theta})$ 联系起来，从而将数值结果转换为分类结果，简单来说，其是利用线性回归模型的预测结果去逼近真实标记的对数几率

Logistic 回归根据分类数据的类别，分为以下三种情况：

  • 二元 Logistic 回归：分类数据为两类（例如：有/没有）
  • 多元无序 Logistic 回归：分类数据超过两类，且类别间没有对比意义（例如：一线城市、二线城市、三线城市）
  • 多元有序 Logistic 回归：分类数据超过两类，且类别间有对比意义（例如：喜欢、不喜欢、无所谓）

需要注意的是，这里的元，指的不是自变量的个数，而是因变量的取值范围

本文仅介绍二元 Logistic 回归，关于多元 Logistic 回归，详见：多元 Logistic 回归

【假设形式】

假设函数

对于给定的容量为 $n$ 的样本集 $D=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),…,(\mathbf{x_n},y_n)\}$，第 $i$ 组样本中的输入 $\mathbf{x_i}$ 具有 $m$ 个特征值，即：$\mathbf{x_i}=(x_i^{(1)},x_i^{(2)},…,x_i^{(m)})\in \mathbb{R}^m$，输出为 $y_i\in \{0,1\}$，二元 Logistic 回归学习到的模型为 $f(\mathbf{x_i};\boldsymbol{\theta})$，使得 $f(\mathbf{x_i};\boldsymbol{\theta})\simeq y_i$

假设函数 $f(\mathbf{x_i};\boldsymbol{\theta})$ 为：

其中，特征参数 $\boldsymbol{\theta}$ 为 $(m+1)\times 1$ 的列向量，即：

$g(z)$ 为激活函数，就是假说表示，对于不同的问题，根据实际情况来选择不同的激活函数

为了表述方便，对假设函数进行简化，定义一个额外的第 $0$ 个特征量，这个特征量对所有样本的取值全部为 $1$，这使得特征量从过去的 $m$ 个变为 $m+1$ 个，即设：$x_i^{(0)}=1$

那么假设函数就可以写为：

在二元 Logistic 回归中，采用 sigmoid 函数 $\sigma(z)=\frac{1}{1+e^{-z}}$ 作为激活函数，其图像如下：

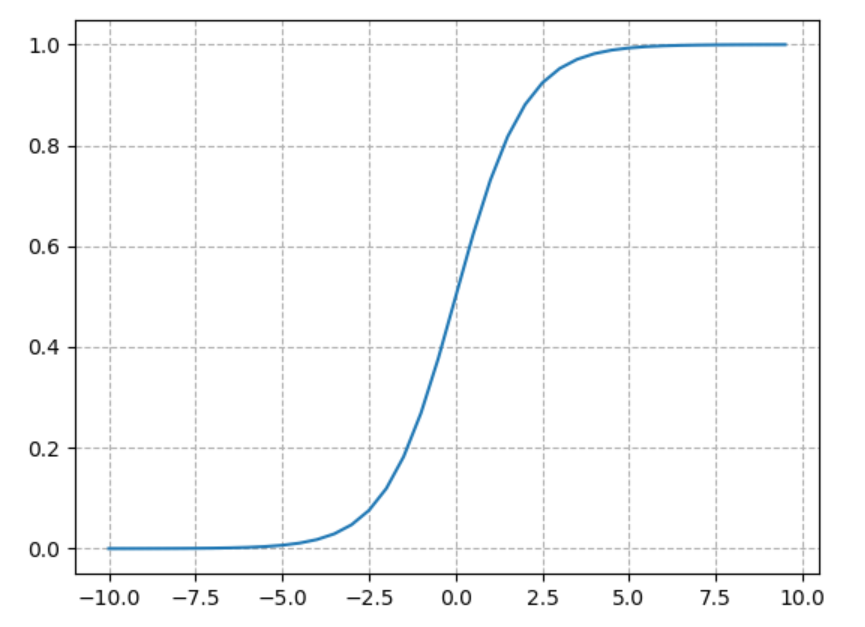
不难看出，sigmoid 函数左侧无限接近于 $0$，右侧无限接近于 $1$，具有很好的对称性，值域 $y \in (0,1)$，正好符合对二分类问题模型的要求

于是，假设函数可以写作：

对数几率形式

对于假设函数 $f(\mathbf{x_i};\boldsymbol{\theta})=\frac{1}{1+e^{-\boldsymbol{\theta}^T\mathbf{x_i}}}$，将假设函数 $f(\mathbf{x_i};\boldsymbol{\theta})$ 的值 $\hat{y_i}$ 记为样本 $\mathbf{x_i}$ 为正例的可能性，则 $1-\hat{y_i}$ 是其为反例的可能性，则两者的比值，称为几率（Odds），其反映了 $\mathbf{x_i}$ 作为正例的相对可能性：

当假设输出标记 $\hat{y_i}$ 是在指数尺度上变化时，可对几率取对数，称为对数几率（Log Odds），即：

将对数几率作为模型逼近的目标，并将假设函数带入，即二元 Logistic 回归模型的对数几率形式：

若将 $\hat{y_i}$ 视为后验概率估计 $P(y_i=1|\mathbf{x_i};\boldsymbol{\theta})$，即在给定概率参数为 $\boldsymbol{\theta}$ 时，对具有 $\mathbf{x_i}$ 特征的条件下 $y_i=1$ 时的概率，即：

那么对于二分类问题，由于输出值非 $0$ 即 $1$，故而可计算出 $y_i=0$ 的概率，即：

那么对数几率可写为：

后验概率形式

对于对数几率 $\ln \frac{P(y_i=1|\mathbf{x_i};\boldsymbol{\theta})}{P(y_i=0|\mathbf{x_i};\boldsymbol{\theta})}=\boldsymbol{\theta}^T\mathbf{x_i}$ 中的 $P(y_i=1|\mathbf{x_i};\boldsymbol{\theta})$ 有：

进而可得：

即：

由于 $y_i$ 只能取 $0$ 或 $1$，那么可以将上面两个式子合写为一个，即二元 Logistic 回归模型的后验概率形式：

【损失函数】

引入

在多元线性回归模型中，当批量使用梯度下降法求解时，损失函数为：

在二元 Logistic 回归中，将假设函数 $\hat{y_i}=\frac{1}{1+e^{-\boldsymbol{\theta}^T\mathbf{x_i}}}$ 带入上述的代价函数里，并画出代价函数的图像，会发现可能是一个类似下图的非凸函数，即有许多局部最优值，如果将梯度下降法用在这样一个函数上，无法保证其能收敛到全局最小值

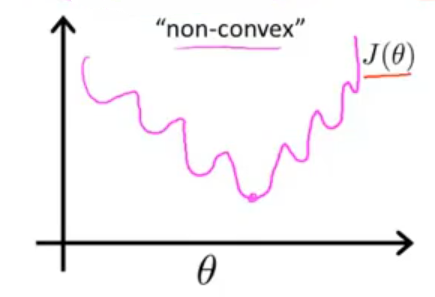
因此，为了保证使用梯度下降法使得代价函数收敛到全局最小值，代价函数需要是一个凸函数，那么就要另找一个不同的代价函数

损失函数

对于得到的二元 Logistic 回归模型的后验概率形式：

采用最大似然法（Maximum Likelihood Method）来估计 $\boldsymbol{\theta}$，即对于给定的容量为 $n$ 的训练集 $D=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),…,(\mathbf{x_n},y_n)\}$，可得到似然函数：

在 $\boldsymbol{\theta}$ 的所有可能取值中找一个使得似然函数取到最大值，这时求得的解就是最大似然估计，即：

由于带连乘运算的似然函数 $L(\boldsymbol{\theta})$ 不好优化，考虑到似然函数的取值范围为 $(0,1)$，那么对似然函数取自然对数不影响其单调性，同时为将最大化问题转为最小化问题，再对取自然对数后的似然函数进行取反，这样就得到了二元 Logistic 回归的损失函数：

此时的损失函数 $J(\boldsymbol{\theta})=-\sum\limits_{i=1}^n \big[ y_i \ln \hat{y_i} + (1-y_i) \ln (1-\hat{y_i}) \big] $，就是整个训练集的损失函数

下面继续对损失函数 $J(\boldsymbol{\theta})$ 进行化简，考虑使用对数几率 $\ln \frac{\hat{y_i}}{1-\hat{y_i}}=\boldsymbol{\theta}^T\mathbf{x_i}$ 进行表示，则有：

即：

接下来要做的，就是要最小化代价函数，为训练集拟合出参数，即：

【批量梯度下降法求解】

使用批量梯度下降法来最小化代价函数：

即将下列公式重复直到收敛为止：

关于批量梯度下降法的具体介绍，详见：梯度下降法

【决策边界】

决策边界（Decision Boundary）是分类问题中假设函数的一个属性，其决定于 $\boldsymbol{\theta}$ 参数，一旦通过训练集拟合出了 $\boldsymbol{\theta}$ 参数，就确定了决策边界

首先来看假设函数：

接着给出 sigmoid 函数的图像，来看一下假设函数何时会预测 $y=0$，何时又会预测 $y=1$

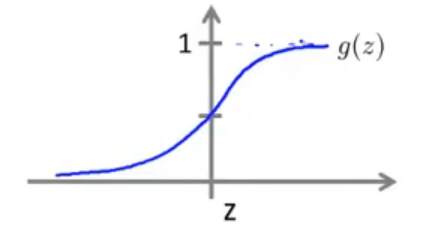
根据 sigmoid 函数图像的对称性，可以认为，只要假设函数输出 $y=1$ 的概率大于或等于 $0.5$，那么意味着 $y=1$，相反地，只要假设函数输出 $y=0$ 的概率小于 $0.5$，那么意味着 $y=0$，即：

也就是说，只要 $\boldsymbol{\theta}^T\mathbf{x_i} \geq 0$，那么 $\hat{y_i} \geq 0.5$，就预测 $y=1$，同理，只要 $\boldsymbol{\theta}^T\mathbf{x_i} < 0$，那么 $\hat{y_i} < 0.5$，就预测 $y=0$

而决策边界，是一条直线，其将预测值为 $1$ 和 $0$ 的两个区域分隔开来，这一条线对应的就是 $\hat{y_i}=0.5$，即 $\boldsymbol{\theta}^T\mathbf{x_i}=0$ 时所对应的线

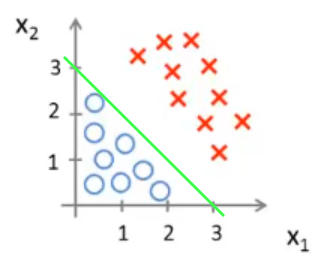
如下图，假设有一个存在两个特征的模型：$\hat{y_i}=g(\theta_0+\theta_1x_1+\theta_2x_2)$

通过训练集拟合出的 $\boldsymbol{\theta}=[-3,1,1]^T$，则：

  • 当 $\boldsymbol{\theta}^T\mathbf{x_i} \geq 0$，即：$-3+x_1+x_2 \geq 0$ 时，模型预测 $y=1$

  • 当 $\boldsymbol{\theta}^T\mathbf{x_i} < 0$，即：$-3+x_1+x_2 < 0$ 时，模型预测 $y=0$

此时，$x_1+x_2=3$ 就是该模型的决策边界

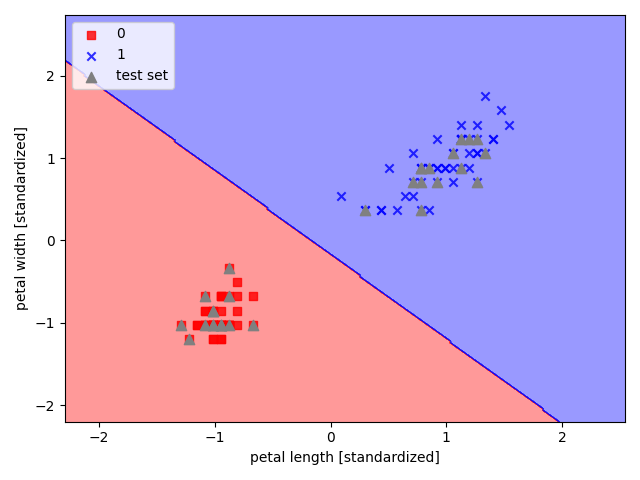
【sklearn 实现】

以 sklearn 中的鸢尾花数据集为例，选取其后两个特征实现二元 Logistic 回归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import confusion_matrix,accuracy_score,classification_report,precision_score,recall_score,f1_score,roc_auc_score
from matplotlib.colors import ListedColormap

# 特征提取
def deal_data():
    iris = load_iris()  # sklearn的鸢尾花数据集
    # iris分为三类，前50行一类，51-100行一类，101-150行一类
    X = iris.data[:100, [2, 3]] # 选用后两个特征作为样本特征
    y = iris.target[:100]  # 取species列，类别
    return X,y

# 数据归一化
def standard_scaler(X_train,X_test):
    sc = StandardScaler() # 初始化一个sc对象去对数据集作变换
    scaler = sc.fit(X_train) # 归一化，存有计算出的均值和方差
    X_train_std = scaler.transform(X_train) # 利用 scaler 进行标准化
    X_test_std = scaler.transform(X_test) # 利用 scaler 进行标准化
    return X_train_std, X_test_std

# 模型训练
def train_model(X_train_std, y_train):
    # 建立Logistic回归模型
    model = LogisticRegression(random_state=0)
    # 训练
    model.fit(X_train_std, y_train)
    return model

# 模型评估
def estimate_model(y_pred, y_test, model):
    # 混淆矩阵
    cm2 = confusion_matrix(y_test,y_pred) 
    # 准确率
    acc = accuracy_score(y_test,y_pred)
    # 正确分类的样本数
    acc_num = accuracy_score(y_test,y_pred,normalize=False)
    # 分类报告
    class_report = classification_report(y_test, y_pred,target_names=["类0","类1"])
    # 精确率
    p = precision_score(y_test,y_pred)
    # 召回率
    r = recall_score(y_test,y_pred)
    # F1得分
    f1 = f1_score(y_test,y_pred)
    # ROC-AUC
    auc = roc_auc_score(y_test,y_pred)
 
    indicators = {"cm2": cm2, "acc": acc, "acc_num": acc_num, "class_report": class_report, "p": p, "r": r, "f1": f1, "auc": auc}
    return indicators

# 可视化
def visualization(X, y, classifier, test_id=None, resolution=0.02):
    # 创建 color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])

    # 绘制决策边界
    x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1  # 第一个特征取值范围作为横轴
    x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1  # 第二个特征取值范围作为纵轴
    xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution), np.arange(
        x2_min, x2_max, resolution))  # reolution为网格剖分粒度
    # 对组合的特征进行预测，ravel为数组展平
    Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
    Z = Z.reshape(xx1.shape)  # Z是列向量
    # x和y为两个等长一维数组，z为二维数组，指定每一对xy所对应的z值
    plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
    plt.xlim(xx1.min(), xx1.max())  # 对等高线间的区域进行填充
    plt.ylim(xx2.min(), xx2.max())  # 对等高线间的区域进行填充

    # 全数据集，不同类别样本点的特征作为坐标(x,y)，用不同颜色画散点图
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8,
                    c=cmap(idx), marker=markers[idx], label=cl)

    # # 高亮测试集
    if test_id:
        X_test, y_test = X[test_id, :], y[test_id]
        # c设置颜色，测试集不同类别的实例点画图不区别颜色
        plt.scatter(x=X_test[:, 0], y=X_test[:, 1], alpha=1.0,
                    c='gray', marker='^', linewidths=1, s=55, label='test set')

    plt.xlabel('petal length [standardized]')
    plt.ylabel('petal width [standardized]')
    plt.legend(loc='upper left')
    plt.tight_layout()
    plt.show()

if __name__ == "__main__":
    # 特征提取
    X, y = deal_data()

    # 简单交叉验证
    X_train, X_test, y_train, y_test = train_test_split(
        X, y, test_size=0.3, random_state=0)

    # 数据标准化
    X_train_std, X_test_std = standard_scaler(X_train, X_test)

    # 模型训练
    model = train_model(X_train_std, y_train)

    # 预测结果
    y_pred = model.predict(X_test_std)
    print("y test:", y_test)  # 测试集y值
    print("y pred:", y_pred)  # 预测y值

    # 模型评估
    indicators = estimate_model(y_pred, y_test, model)
    cm2 = indicators["cm2"]
    print("混淆矩阵：\n", cm2)
    acc = indicators["acc"]
    print("准确率：", acc)
    acc_num = indicators["acc_num"]
    print("正确分类的样本数：", acc_num)
    class_report = indicators["class_report"]
    print("分类报告：\n", class_report)
    p = indicators["p"]
    print("精确率：", p)
    r = indicators["r"]
    print("召回率：", r)
    f1 = indicators["f1"]
    print("F1得分：", f1)
    auc = indicators["auc"]
    print("AUC：", auc)

    # 可视化
    X_combined_std = np.vstack((X_train_std, X_test_std))
    y_combined = np.hstack((y_train, y_test))
    # classifier为分类器，test_id为测试集序号
    visualization(X_combined_std, y_combined, classifier=model, test_id=range(70, 100))
感谢您对我的支持，让我继续努力分享有用的技术与知识点！