Reference
【概述】
最小角回归法(Least Angle Regression,LAR),是一种针对于线性回归问题,快速进行特征选择和回归系数计算的迭代算法,其被广泛推广用于求解线性回归以及 Lasso 回归问题
其核心思想是:将回归目标向量依次分解为若干组特征向量的线性组合,最终使得与所有特征均线性无关的残差向量最小
可见,最小角回归法的关键在于选择正确的特征向量分解顺序和分解系数
为更好地介绍最小角回归法,首先介绍相关的前向选择算法(Forward Selection Algorithm)与前向逐步算法(Forward Stagewise Algorithm)
【残差向量】
对于忽略偏置项的回归问题:
$x^{(1)},x^{(2)},…,x^{(m)}$ 为特征向量,$\theta^{(1)},…,\theta^{(m)}$ 为预求的回归系数
定义残差向量 $y_i$ 为进行第 $i$ 次特征向量线性组合后,与目标向量 $y$ 的向量差
那么,初始残差向量有:
对于忽略偏置项的回归问题 $y= \theta^{(1)} x^{(1)} + \theta^{(2)} x^{(2)}$,特征向量与初始残差向量如下图

【前向选择算法】
前向选择算法(Forward Selection Algorithm)是一种贪婪地对目标向量进行特征分解的算法,常用于回归模型的自变量选择,其是一种迭代算法,每次将候选的自变量逐个引入回归方程中,逐个选择自变量
对于回归问题 $y=\theta^{(0)} + \theta^{(1)} x^{(1)} + \theta^{(2)} x^{(2)} + … + \theta^{(m)} x^{(m)}$,其初始残差向量为:
在第一轮中,会选择一个与 $y_0$ 余弦相似度最高的特征向量 $x^{(M_0)}$,并将 $y_0$ 在该特征向量的方向上进行投影,以得到第二轮的残差向量 $y_1=y_0-\theta^{(M_0)}x^{(M_0)}$
之后,进行迭代,对于第 $k$ 轮迭代来说,会在该轮迭代前未被选用过的特征向量中,选择一个与当前残差向量 $y_{k-1}$ 余弦相似度最高的特征向量 $x^{(M_k)}$,然后在该特征向量的方向上进行投影,最后令该轮的残差向量 $y_{k-1}$ 减去该轮的投影向量 $x_{M_k}=\theta^{(M_k)}x^{(M_k)}$,以得到该轮的目标残差向量 $y_k$,即:
直到无多余特征向量,或无目标残差向量,或残差向量足够小时,终止迭代
对于忽略偏置项的回归问题 $y= \theta^{(1)} x^{(1)} + \theta^{(2)} x^{(2)}$,前向选择算法迭代过程如下图
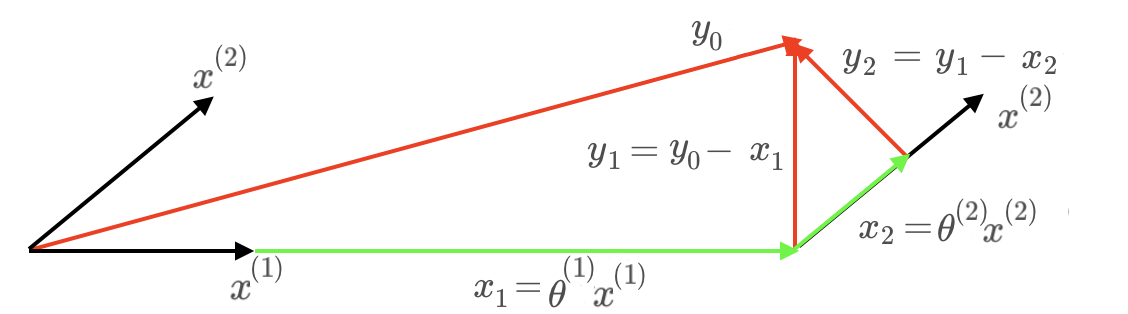
前向选择算法简单粗暴,各特征向量最多使用一次,每轮的目标残差方向均与上一轮采用的特征向量方向正交,但由于其忽略了各特征向量间可能存在的线性关系,仅作盲目的依次投影,因此计算较为粗糙,只能给出局部近似解
【前向逐步算法】
前向逐步算法(Forward Stagewise Algorithm)与前向选择算法的基本思想一致,但其没有盲目的进行投影,而是采用了小步试错的方法,以保证每一步分解的合理性
对于回归问题 $y=\theta^{(0)} + \theta^{(1)} x^{(1)} + \theta^{(2)} x^{(2)} + … + \theta^{(m)} x^{(m)}$,其初始残差向量为:
在第 $k$ 轮迭代中,其选择一个与本轮目标残差向量 $y_{k-1}$ 余弦相似度最高的特征向量 $x^{(M_k)}$,然后在该方向上移动一小步 $\epsilon x^{(M_k)}$,从而得到下一轮的目标残差向量 $y_{k}$,即:
直到无目标残差向量,或残差向量足够小时,终止迭代
对于忽略偏置项的回归问题 $y= \theta^{(1)} x^{(1)} + \theta^{(2)} x^{(2)}$,前向逐步算法迭代过程如下图
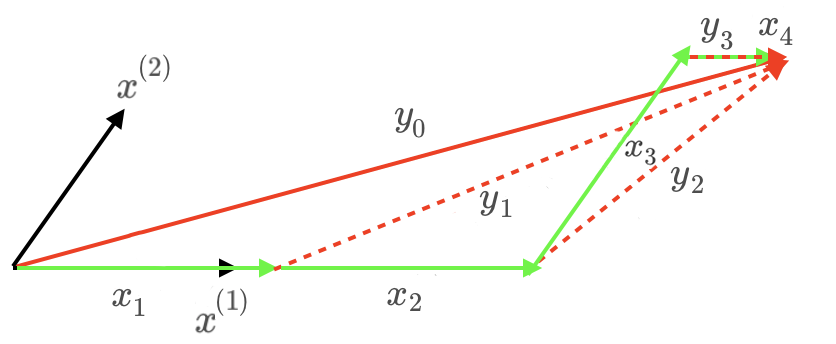
前向逐步算法中,每轮的候选特征向量均为全部的特征向量,因此每个特征向量可能会被多次使用,同时,当 $\epsilon$ 足够小时,可以得到一个较为精确的解,但此时计算量很大
【最小角回归法】
对于前向选择算法来说,其相较于前向逐步算法速度快,但准确性不高;对于前向逐步算法来说,其相较于前向选择算法准确性高,但速度不快
最小角回归法(Least Angle Regression,LAR)就是前向选择算法的快速性与前向逐步算法的准确性的折中
对于回归问题 $y=\theta^{(0)} + \theta^{(1)} x^{(1)} + \theta^{(2)} x^{(2)} + … + \theta^{(m)} x^{(m)}$,其初始残差向量为:
在第一轮中,会选择一个与 $y_0$ 余弦相似度最高的特征向量 $x^{(M_0)}$,并在特征向量 $x^{(M_0)}$ 的方向上移动某个步长 $\omega^{(0)}$,得到此时的目标残差向量 $y_1=y_0-\omega^{(0)}x^{(M_0)}$,要求 $y_1$ 与特征向量 $x^{(M_0)}$ 和余弦相似度第二高的特征向量 $x^{(M_0’)}$ 的相关性相等,即令 $y_1$ 等于 $x^{(M_0)}$ 和 $x^{(M_0’)}$ 的角平分向量
之后,进行迭代,对于第 $k$ 轮迭代来说,会在该轮迭代前未被选用过的特征向量中,选择一个与当前残差向量 $y_{k-1}$ 余弦相似度最高的特征向量 $x^{(M_k)}$,并在上一轮的角平分向量的方向即当前残差向量 $y_{k-1}$ 上移动某个步长 $\omega^{(k)}$,得到该轮的目标残差向量 $y_k=y_{k-1}-\omega^{(k)}x^{(M_k)}$,要求 $y_k$ 与之前被选用过的特征向量的相关性相等,即令 $y_k$ 等于之前被选用过的特征向量的角平分向量
直到无多余特征向量,或无目标残差向量,或残差向量足够小时,终止迭代
对于忽略偏置项的回归问题 $y= \theta^{(1)} x^{(1)} + \theta^{(2)} x^{(2)}$,最小角回归算法迭代过程如下图
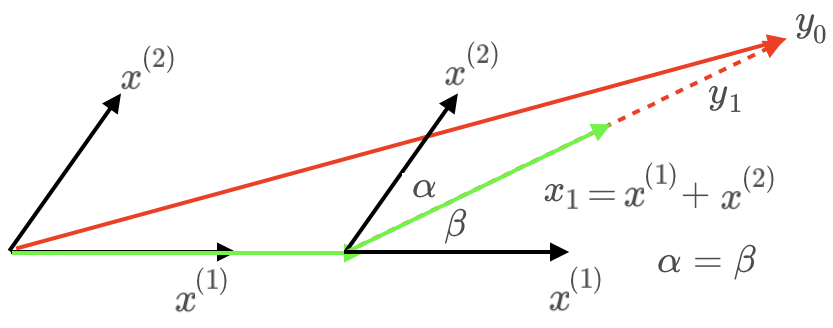
在最小角回归算法中,各特征向量最多使用一次,其通过准确得到每步最优的分解长度以保证计算的准确性和速度
此外,其具有以下特点:
- 特别适合特征维度 $m$ 远高于样本数 $n$ 的情况
- 最坏计算复杂度和最小二乘法相同,但平均计算速度与前向选择算法一样
- 可以产生分段线性结果的完整路径,在模型的交叉验证中极为有用
- 迭代方向是基于目标残差方向,很容易受到噪声的影响

