常见的激活函数

【概述】

激活函数（Activation Function），是用于将权值结果转换为分类结果的一类函数，目前常用激活函数的地方有两个：

• 逻辑回归（Logistic Regression）
• 神经网络（Neural Network）

在这两种应用中，激活函数都是用于计算一个线性函数，通过计算每个类别可能性的概率，将其权值结果转为分类结果

激活函数的灵感来自于生物神经网络，被认为是神经元对输入的激活程度

最理想的一种形式是单位阶跃函数，其类似一个开关，要么是 $0$，要么是 $1$，即：

$$\epsilon(t)=\left\{\begin{matrix}1 & t\geq 0 \\ 0 & t<0 \end{matrix}\right.$$

但在实际应用中，由于单位阶跃函数具有不连续、不光滑的性质，因此一般不使用单位阶跃函数，只是将其作为激活函数思想的来源

【Sigmoid】

一般形式

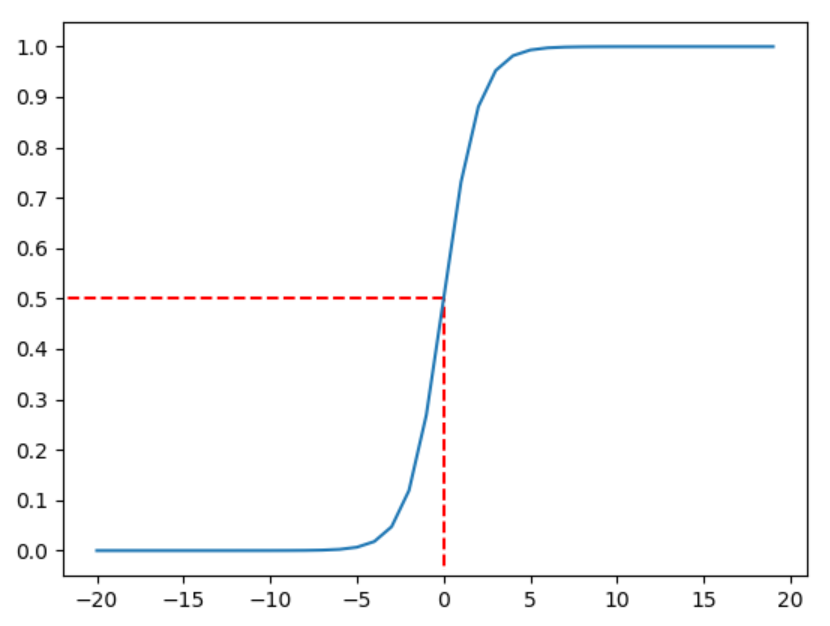
S 型函数（Sigmoid），其常用于表示 Yes/No 这类的信息，多用于过滤数据，是一个典型的”门”，在 Logistic 回归中广泛应用，因此又称 Logistic 函数

其表达式为：

$$\sigma(x) = \frac{e^x}{1+e^x} = \frac{1}{1+e^{-x}} , x \in (0,1)$$

该函数图像左侧无限接近于 $0$，右侧无限接近于 $1$，在 $x=0$ 处，有 $\sigma(x)=0.5$，具有良好的对称性

微分

对于 $\sigma(x)$ 函数，下面给出其微分形式的推导：

$$\begin{align*}\frac{\partial \sigma(x)}{\partial x} &= \frac{1' \cdot (1+e^{-x}) - 1 \cdot (1+e^{-x})'}{(1+e^{-x})^2} \\ &= \frac{e^{-x}}{(1+e^{-x})^2} \\ &= \frac{e^{-x}}{1+e^{-x}} \cdot \frac{1}{1+e^{-x}} \\ &= \frac{e^{-x}+1-1}{1+e^{-x}} \cdot \frac{1}{1+e^{-x}} \\ &= (1 - \frac{1}{1+e^{-x}}) \cdot \frac{1}{1+e^{-x}} \\ &= (1-\sigma(x))\sigma(x) \end{align*}$$

即：

$$\sigma'(x)=(1-\sigma(x))\sigma(x)$$

【Tanh】

一般形式

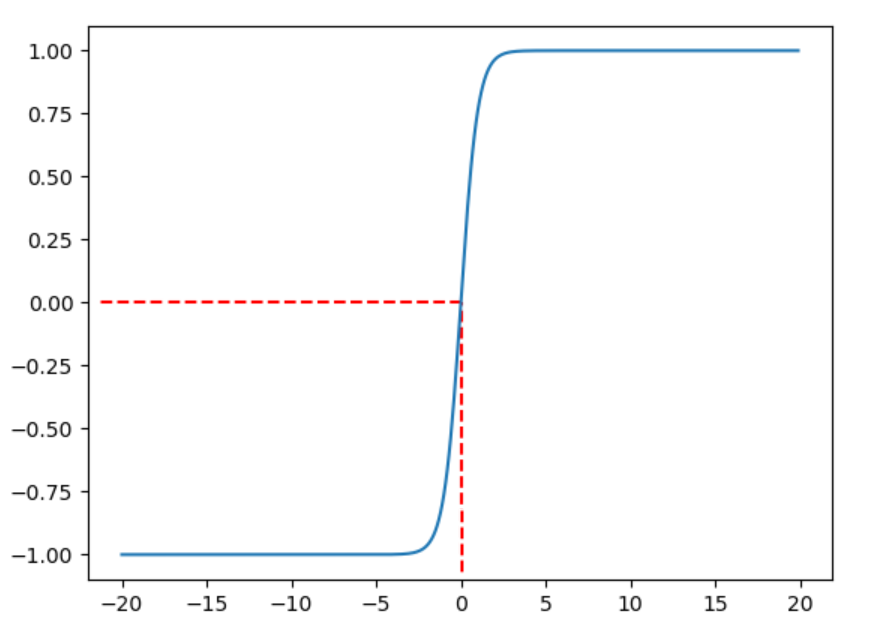
双曲正切函数（Hyperbolic Tangent，Tanh），与 Sigmoid 函数相似，其同样可以表示 Yes/No 的信息，但其对值域进行了扩充，使得可以表达三种状态，例如：不喜欢(-1)/无感(0)/喜欢(1)

该函数多用于输出数据，并且输出的数据最终会利用 softmax 函数进行计算

该函数是由双曲正弦 $\sinh(x)=\frac{e^x-e^{-x}}{2}$ 和双曲余弦 $\cosh(x)=\frac{e^x+e^{-x}}{2}$ 这两种基础双曲函数推导而来，即：

$$\begin{align*}\tanh(x) &= \frac{\sinh(x)}{\cosh(x)} \\ &= \frac{e^x-e^{-x}}{e^x+e^{-x}} \\ &= \frac{e^{2x}-1}{e^{2x}+1} \end{align*}$$

即：

$$\tanh(x)=\frac{e^{2x}-1}{e^{2x}+1},x \in (-1,1)$$

该函数图像与 $\sigma(x)$ 函数十分相似，左侧无限接近于 $-1$，右侧无限接近于 $1$，在 $x=0$ 处，有 $tanh(x)=0$，具有良好的对称性

微分

对于 $\tanh(x)$ 函数，下面给出其微分形式的推导：

$$\begin{align*}\frac{\partial \tanh(x)}{\partial x} &= (\frac{e^{2x}-1}{e^{2x}+1})' \\ &= (1 - \frac{2}{e^{2x}+1})' \\\ &= \frac{(-2)'(e^{2x}+1) - (-2)(e^{2x}+1)'}{(e^{2x}+1)^2} \\\ &= \frac{2(e^{2x}+1)'}{(e^{2x}+1)^2} \\ &= \frac{4e^{2x}}{(e^{2x}+1)^2} \\ &= \frac{(e^{2x}+1)^2 - (e^{2x}-1)^2}{(e^{2x}+1)^2} \\\ &= 1-(\frac{e^x-1}{e^x+1})^2 \\ &= 1-\tanh(x)^2 \end{align*}$$

即：

$$\tanh'(x)=1-\tanh(x)^2$$

【softmax】

引入

softmax 函数又称归一化指数函数，其是 sigmoid 函数在多分类问题上的推广，目的是将多分类的结果以概率的形式展示出来

我们知道预测出来的概率满足两个性质：预测概率为非负、各种预测概率之和等于 $1$，而 softmax 就是将负无穷到正无穷上的预测结果按照这两个步骤来转换概率的

指数函数 $e^x$ 的值域取值范围是 $(0,+\infty )$，因此 softmax 函数的第一步就是将模型预测结果转换到指数函数上，以保证概率的非负性

之后，为确保各类预测结果的概率和为 $1$，我们将转换后的结果进行归一化处理，将转化后的结果除以转化后的结果之和，即转化后结果占总数的百分比

基本形式

对于给定 $K$ 维向量 $\mathbf{z}=[z^{(1)},z^{(2)},…,z^{(K)}]$，其中第 $i$ 个分量经过 softmax 函数处理后有：

$$\text{softmax}(z^{(i)})=\frac{e^{z^{(1)}}}{\sum\limits_{k=1}^K e^{x^{(k)}}}$$

实例

举例来说，假设一个三分类模型的预测结果为 $z_1=3,z_2=1,z_3=-3$，使用 softmax 函数进行处理

Step1：将预测结果利用指数函数转为非负数，有：

$$\begin{matrix}x_1=e^{z_1} = e^3 = 20 \\ x_2=e^{z_2} = e^1 = 2.7 \\ x_3=e^{z_3} = e^{-3} = 0.05 \end{matrix}$$

Step2：计算转化后的结果之和：

$$\text{sum} = \sum_{j=1}^3 x_i = 20+2.7+0.05 = 22.75$$

Step3：进行归一化处理：

$$\begin{matrix}y_1 = \frac{x_1}{\text{sum}} = \frac{20}{22.75} = 0.88 \\ y_2 = \frac{x_2}{\text{sum}} = \frac{2.7}{22.75} = 0.12 \\ y_3 = \frac{x_3}{\text{sum}} = \frac{0.05}{22.75} \approx 0 \end{matrix}$$

上述过程的处理流程图如下：

【ReLU】

修正线性单元（Rectified Linear Unit，ReLU），在神经网络中十分常用，其符合人的神经节运作方式，在 ReLu 函数的左端是抑制的，右端是打开的

其表达式为：

$$\text{ReLu}(x)=\max(0,x)\left\{\begin{matrix}0 & x<0 \\ x & x \geq 0 \end{matrix}\right.$$

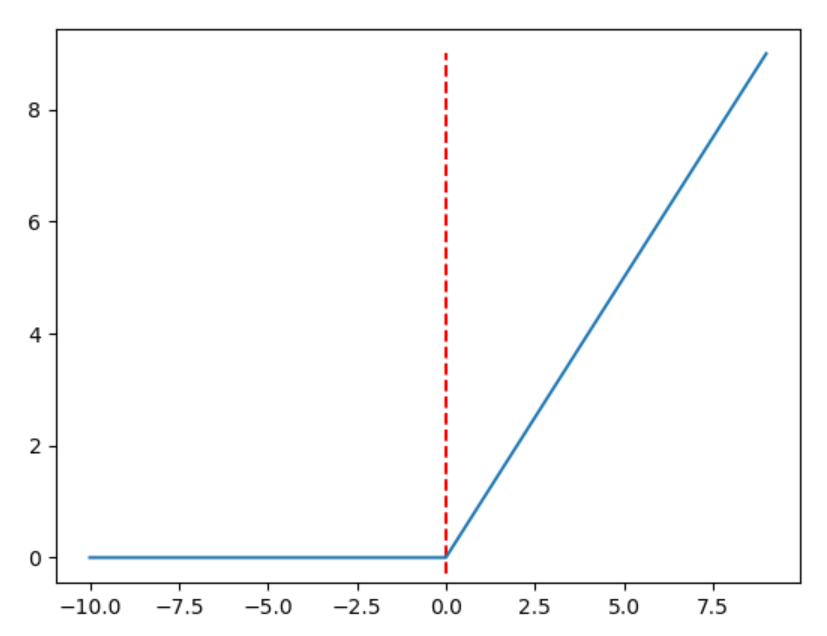
很容易看出，该函数梯度在左端为 $0$，在右端为 $1$，对于正值较少的数据，处理能力更强，很好的避免了梯度消失问题

梯度消失问题是指，在神经网络中，当前隐藏层的学习速率低于后面隐藏层的学习速率，即随着隐藏层数目的增加，分类准确率反而下降了