Reference:
【网络结构】
卷积神经网络由一个或多个卷积层、池化层以及全连接层等组成,其也可以使用反向传播算法进行训练,其架构如下
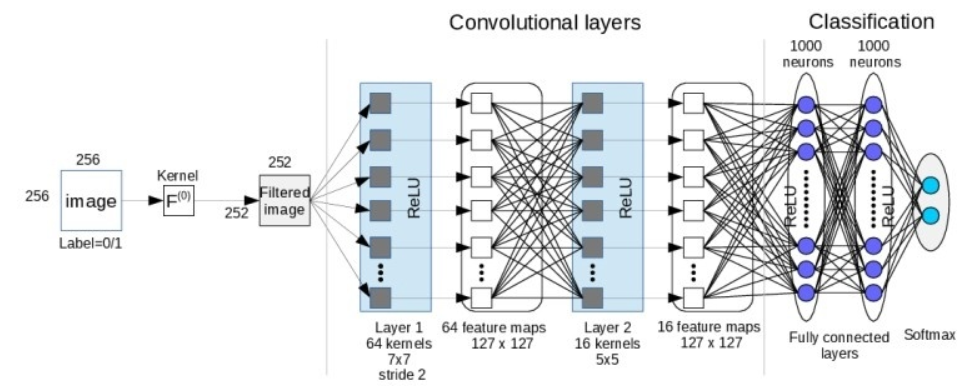
【输入层】
与全连接神经网络相比,卷积神经网络的输入层输入的是一个 $n\times m \times 3$ 的 RGB 图像,而全连接神经网络的输入是 $n×1$ 维的向量
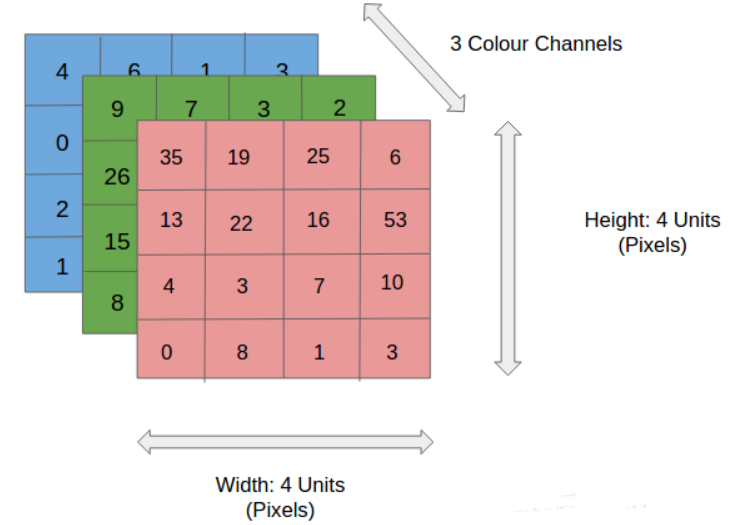
【卷积层】
输入与输出
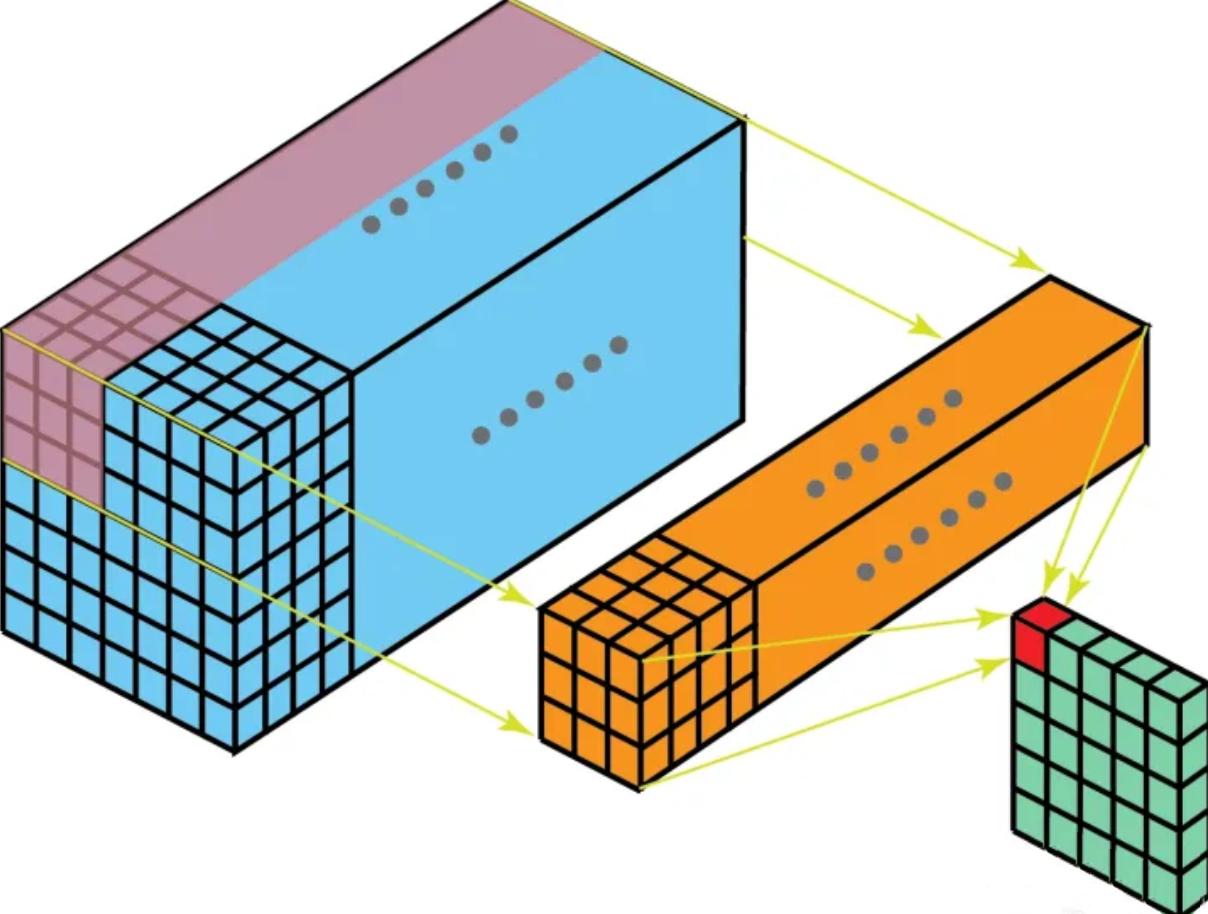
卷积层(Convolutional Layer)是构建卷积神经网络的核心层,它产生了网络中大部分的计算量,其通过滤波器的卷积运算来提取输入的特征,即计算输入图像区域与滤波器的点积和作为该层的输出
此外,网络越深,使用的滤波器就越多,而拥有的滤波器越多,获得的边缘和特征检测就越多
对于输入尺寸为 $H_i\times W_i \times c_i$ 的图像,设网络中某卷积层的滤波器数量为 $K$,卷积核的大小为 $F$,零填充大小为 $P$,步长为 $S$,那么对于输出图像大小 $H_o\times W_o \times c_o$,有:
范式
假设卷积神经网络第 $l$ 层为卷积层,上一层的输出 $A^{[l-1]}$ 的大小为 $n_h^{[l-1]}\times n_w^{[l-1]}\times n_c^{[l-1]}$,即其接受的输入为:
- 图像高度:$n_h^{[l-1]}$
- 图像宽度:$n_w^{[l-1]}$
- 图像通道数:$n_c^{[l-1]}$
而对于该卷积层 $L_l$,有如下参数:
- 卷积核大小:$f^{[l]}$
- 零填充大小:$p^{[l]}$
- 步长大小:$s^{[l]}$
- 滤波器个数:$n_c^{[l]}$
故有:
- 单个滤波器大小:$f^{[l]} \times f^{[l]} \times n_c^{[l-1]}$
- 所有的滤波器大小(连接权重维度):$f^{[l]}\times f^{[l]} \times n_c^{[l-1]} \times n_c^{[l]}$
- 偏置项维度:$1\times 1\times 1\times n_c^{[l]}$
记连接权重为 $W^{[l]}$,偏置为 $\mathbf{b}^{[l]}$,上一层输出值 $A^{[l-1]}$ 那么有权重累计:
其中,$*$ 代表卷积操作,$Z^{[l]}$ 的维度为 $n_h^{[l]}\times n_w^{[l]}\times n_c^{[l]}$
参数个数
在 从全连接神经网络到卷积神经网络 中,介绍了全连接神经网络处理图像带来的问题
使用全连接神经网络处理大尺寸图像时,无疑会造成参数过多效率低下,训练困难,那么,下面计算一下使用卷积神经网络时的参数个数
假设卷积神经网络中只有一层卷积层,该卷积层中有 $10$ 个滤波器,每个滤波器大小为 $3\times 3\times 3$
那么,对于每个滤波器来说,其有 $3\times 3\times 3$ 个连接权重,$1$ 个偏置项,对于所有滤波器来说,参数个数为:
即使图片任意大小,这层的参数也就这么多
从以上角度来看,卷积神经网络无疑极大的减小了参数个数,有助于神经网络的训练
【非线性层】
非线性层(Non-linearity Layer)也被称为激活层,该层一般在卷积层之后,用于对卷机层的输出进行激活处理
通常激活函数会采用 ReLU 函数,但是否加激活函数是根据数据集来决定的,如果是图像类的数据集,需要学习复杂深度特征,那么就需要进行非线性激活
在经过激活函数 $\text{ReLU}(\cdot)$ 后,得到该层输出:
其维度为 $n_h^{[l]}\times n_w^{[l]}\times n_c^{[l]}$
【池化层】
池化层(Pooling Layer)主要对卷积层学习到的特征图进行亚采样(Subsampling)处理,其核心目标是在保证深度的前提下减小特征空间的维度,从而降低后续网络层的输入维度,缩减模型大小,提高计算速度,同时,池化层提高了特征图的鲁棒性,有助于防止过拟合
目前池化层主要有两种方式:
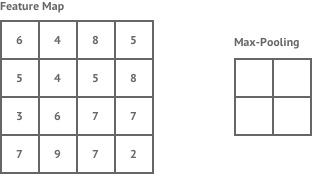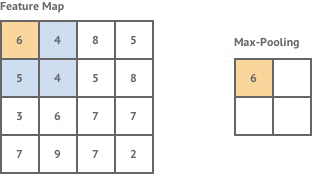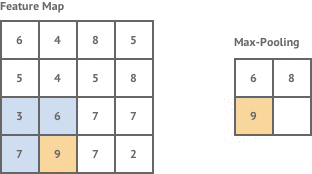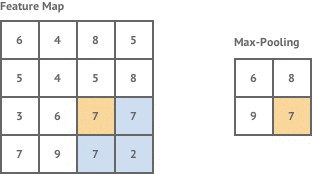
- 最大池化(Max Pooling):取池化窗口中的最大值作为输出
- 平均池化(Average Pooling):取池化窗口内的均值作为输出
如下图所示,是最大池化的过程
【全连接层】
全连接层(Fully Connected Layer,FC Layer)是将池化层输出的特征图展平(Flatten),将每个特征作为神经元的输入,并将其与下一层的神经元连接起来,其与全连接神经网络中的一般操作完全相同
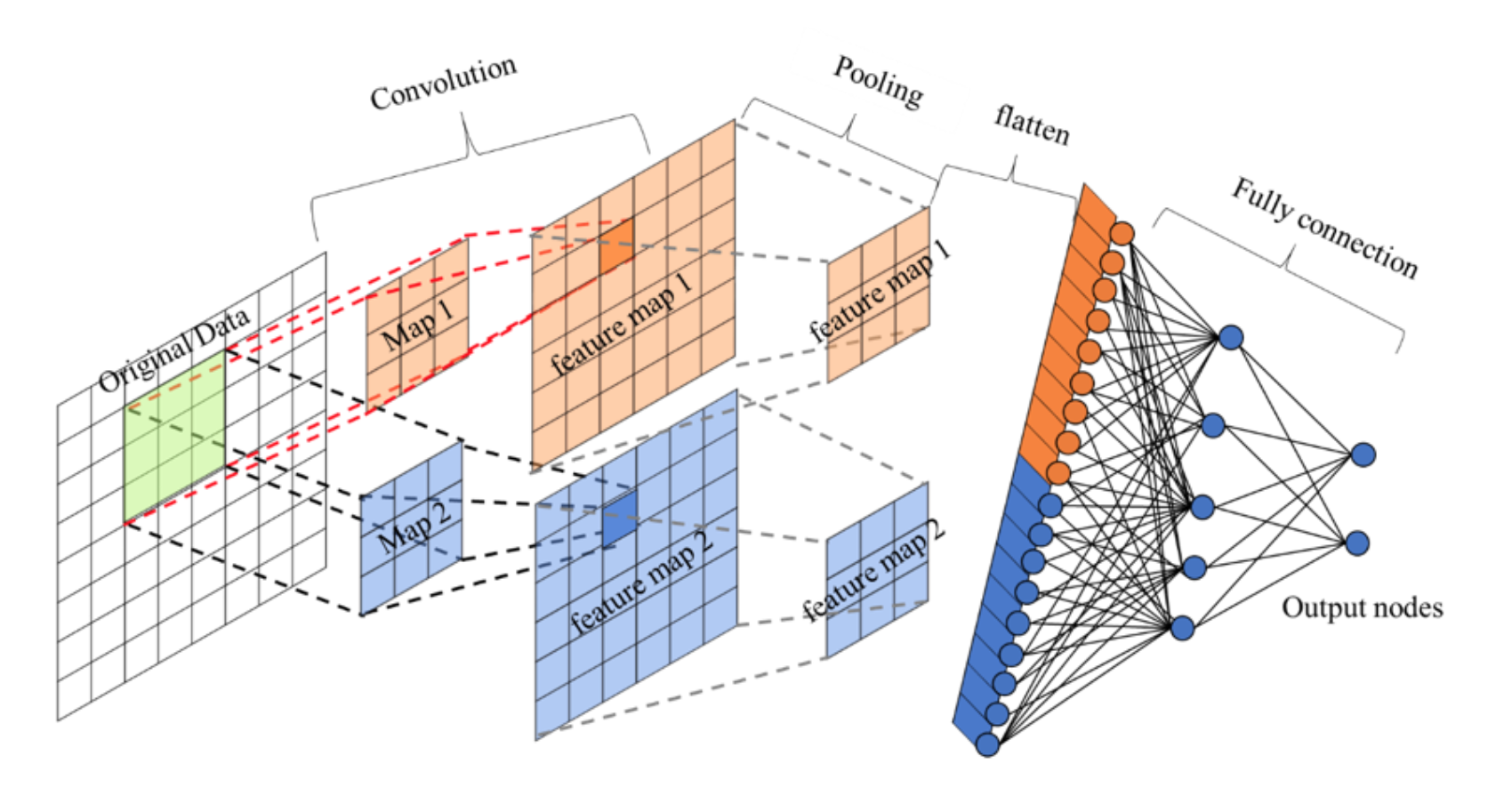
卷积层、非线性层、池化层可以看作 CNN 的特征提取层,将原始数据映射到隐层特征空间,全连接层是将学习到的分布式特征表示映射到样本标记空间
简单来说,对于卷积层、非线性层、池化层学习到的特征图,在通过全连接层后,最终将用于分类、回归等模型任务,全连接层起分类器或回归器的作用
【感受野】
概念
卷积核是基于生物学中感受野(Receptive Field)的概念提出的,在 CNN 中,其是指特征图上的某个点能看到的输入图像的区域,即特征图上的点是由输入图像中感受野大小区域的计算得到的
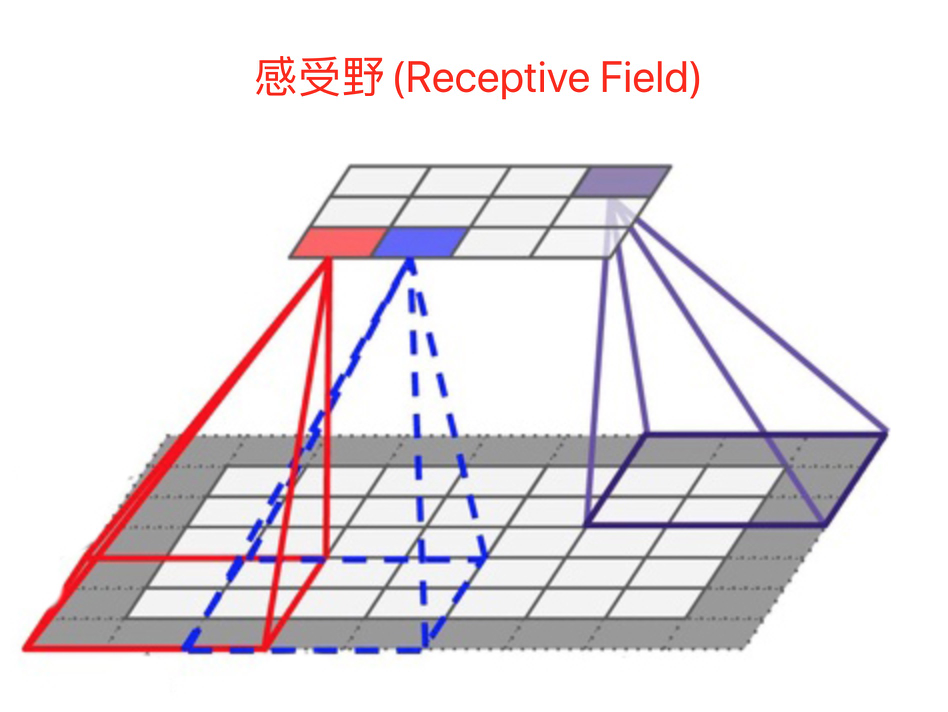
感受野的值越大,表示其能接触到的原始图像范围就越大,也意味着它可能蕴含更为全局,语义层次更高的特征,相反,感受野的值越小,则表示其所包含的特征越趋向局部和细节,因此感受野的值可以用来大致判断每一层的抽象层次
在现流行的一些 CNN 结构中,例如 Faster RCNN,某些参数的设置需要考虑感受野,过大或过小都不好
计算
设 $RF^{[l]}$ 为 CNN 中第 $l$ 层的感受野,$F$ 为卷积核大小,$S^{[l]}$ 表示第 $l$ 层前所有卷积层的步长的乘积,则第 $l+1$ 层的感受野为:
其中,$\text{stride}^{[i]}$ 表示第 $i$ 层滤波器的步长
通过上述公式求取的感受野通常很大,但实际的有效感受野(Effective Receptive Field)往往小于理论感受野,这是因为输入层中边缘点的使用次数明显比中间点要少,两者作出的贡献不同,因此在经过多层的卷积堆叠后,输入层对于特征图点做出的贡献分布呈高斯分布

