卷积核与滤波器

Reference：

• CNN基础知识——卷积（Convolution）、填充（Padding）、步长(Stride)
• 一文看懂卷积运算（convolution）与互相关运算（cross-correlation）的区别
• 卷积核（kernels）与滤波器（filters）的关系
• 卷积神经网络CNN、感受野、边缘检测、卷积层(零填充padding、步长、多通道卷积、多卷积核)、池化层Pooling、全连接层

【卷积核】

卷积核（Convolutional Kernel）是一个大小为 $n\times n$ 的矩阵，用于检测图像中特定的特征，在某一个卷积核对图像进行卷积运算（Convolution）时，就是将卷积核分别与图像的同大小区域进行点乘求和，依次从左到右从上到下滑过图像的所有区域，最终得到特征图（Feature Map）

如下图所示，图像为 $5\times 5$ 的单通道图像，卷积核大小为 $3\times 3$，其从左到右从上到下滑过整个图像，分别计算图像被卷积核盖住的部分的点乘和，最终得到卷积操作后的特征图像

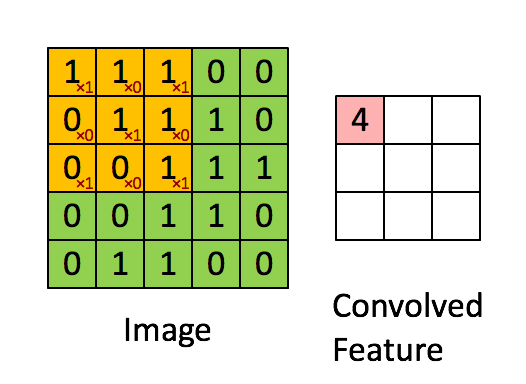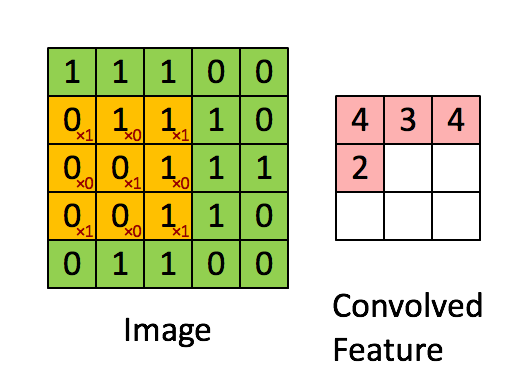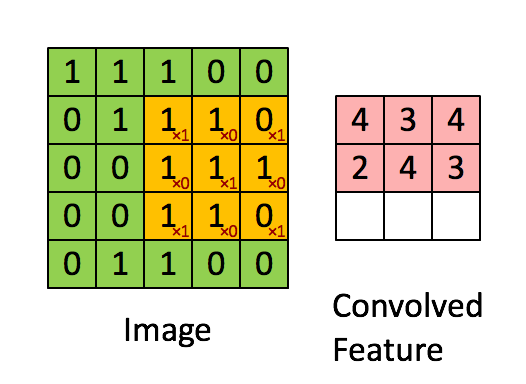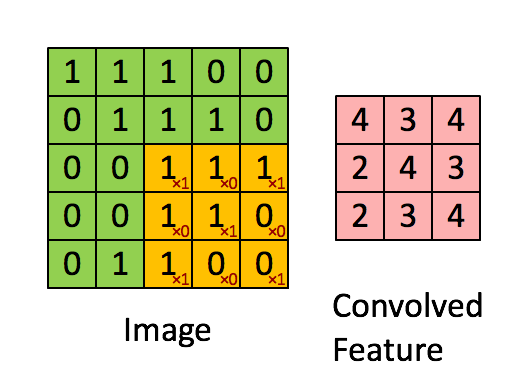
对于输入尺寸为 $N\times N $ 的图像，设卷积核大小为 $F$，那么最终得到的图像大小为：

$$N-F+1$$

此外，卷积核大小 $F$ 一般默认为奇数，其中一个原因是因为这样形成的卷积核有中心，能够轻松定位卷积核的位置

需要注意的是，这里的卷积运算，并不是严格的数学意义上的卷积，实际上是信号处理和图像处理中的互相关运算（Cross-correlation）

【Padding】

零填充

在输入图像与卷积核进行卷积操作时，边缘上的像素永远不会位于卷积核的中心，卷积核也无法扩展到边缘区域以外，也就是说，对于图像边缘的部分只检测了部分像素点，而丢失了图像边界处的众多信息

此外，在进行卷积操作后，输出的特征图的尺寸相较于输入图像的尺寸有所减少，而有时却希望保证输入和输出尺寸相同

为解决上述两个问题，可以在进行卷积操作前，对输入图像的边界进行填充（Padding），即在输入图像对应的矩阵的边界上填充一些值，以增加矩阵大小

为避免 Padding 对图片增加额外的干扰信息，通常会将填充值设为 $0$，这是因为 $0$ 在权重乘积和运算中对最终结果不造成影响，其被称为零填充（0-Padding）

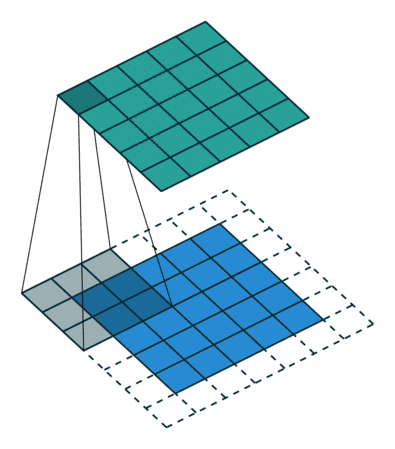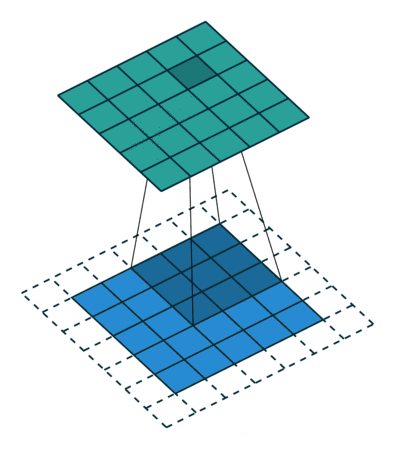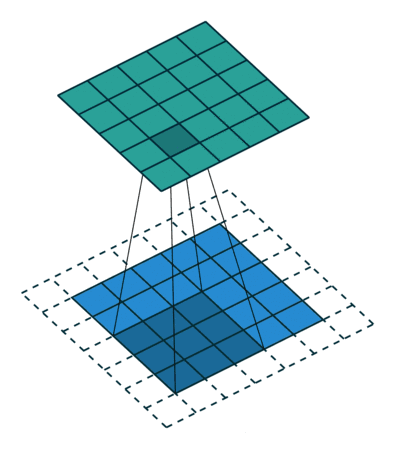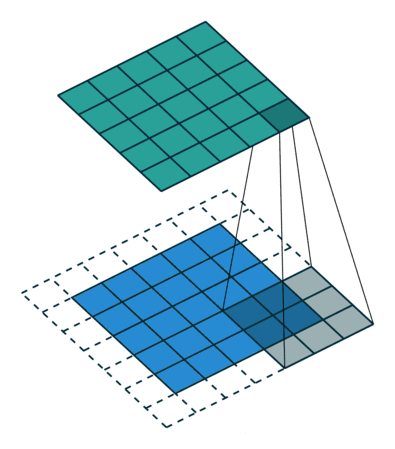
此时，对于输入尺寸为 $N\times N $ 的图像，设卷积核大小为 $F$，零填充层数为 $P$，那么最终得到的图像大小为：

$$N+2P-F+1$$

填充模式

由于进行 Padding 时，并不限制仅填充一层，因此常见的 Padding 有以下三种模式：

1. 空填充（Valid Padding）：当卷积核全部在图像范围内，才进行卷积运算，即零填充层数 $P=0$，最终生成的图像尺寸小于原图像
2. 相同填充（Same Padding）：当卷积核的中心与图像的边角重合时，才进行卷积运算，即零填充层数 $P=\frac{F-1}{2}$，最终生成的图像尺寸与原图像尺寸一致
3. 全填充（Full Padding）：当卷积核与图像有重合范围时，进行卷积运算，即零填充层数 $P=F-1$，最终生成的图像尺寸大于原图像

如下图所示，从左到右分别为空填充、相同填充、全填充

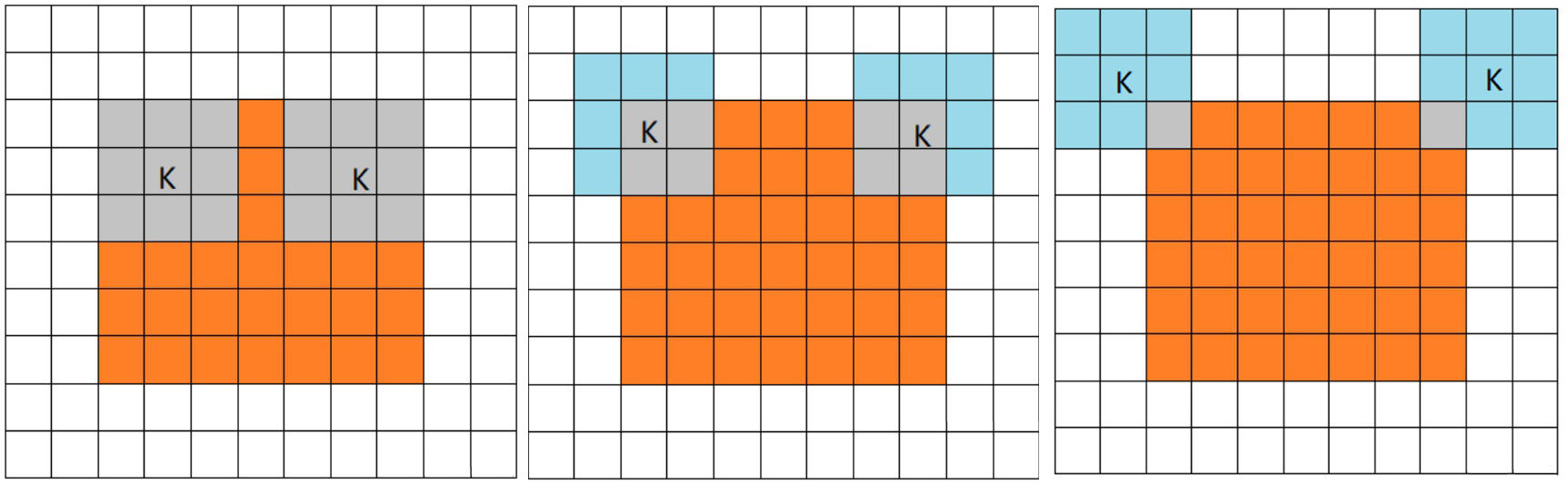
需要注意的是，对于相同填充，零填充层数 $P=\frac{F-1}{2}$，如果卷积核大小 $F$ 不是奇数而是偶数，那么会造成填充不均匀，这也是为什么卷积核默认使用奇数大小的原因之一

【步长】

步长（Stride）是指卷积核每次滑动的大小，其可以成倍的压缩图像信息

在上述的例子中，均是步长为 $1$，在下图中，步长为 $2$

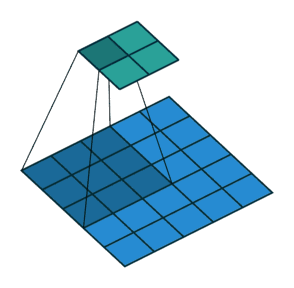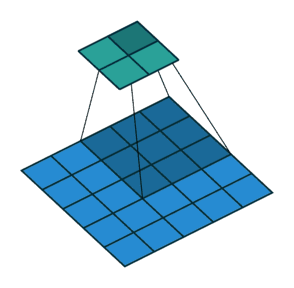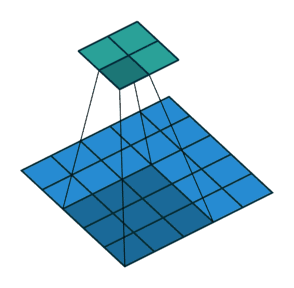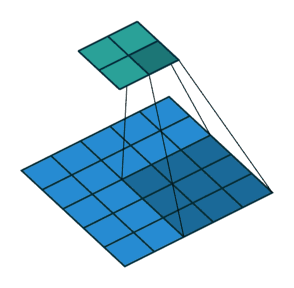
在卷积过程中，使用空填充可以一定程度上来压缩部分信息，使输出尺寸小于输入尺寸，但有时需要成倍的进行压缩，那么就可以修改步长

简单来说，输出尺寸是输入尺寸的 $\frac{1}{\text{stride}}$ 倍

对于输入尺寸为 $N\times N $ 的图像，设卷积核大小为 $F$，零填充层数为 $P$，步长为 $S$，那么最终得到的图像大小为：

$$\Big\lfloor \frac{(N+2P-F)}{S} \Big\rfloor +1$$

---

例如，假设存在一张 $200\times 200 \times 3$ 大小的 RGB 图像，卷积核大小为 $F$，步长为 $1$，为保证最后输出的大小为 $200\times 200$

需要设置的零填充大小为：

$$P = \frac{(N-1)S+F-N}{2} = \frac{199+3-200}{2}=1$$

【滤波器】

结构

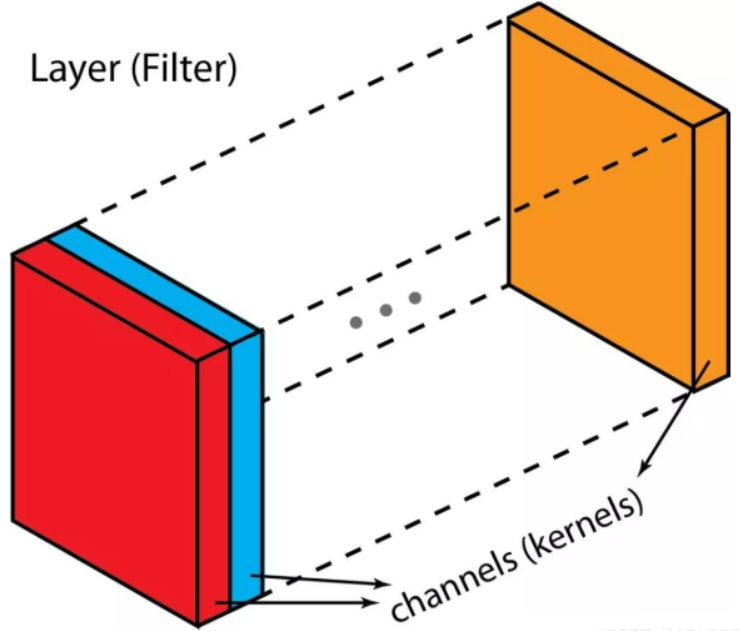
滤波器（Filter），其是由多个卷积核组成的三维矩阵 $n\times n\times c$，多出的一维是通道数 $c$，与输入图像的通道数数量相同

如果输入的是一个 RGB 图像，那么就会有三个通道，滤波器就具有三个卷积核，如果输入的单通道图像，那么滤波器就只有一个卷积核

也就是说，如果输入图像是单通道图像时，滤波器与卷积核是一致，反之，如果输入图像不是单通道图像时，滤波器与卷积核具有不同的结构

多通道卷积

当通道数大于 $1$ 时，滤波器中的卷积核也大于 $1$，此时的滤波器往往被称为多通道卷积，此时每个卷积核需要与输入层对应的通道进行卷积操作，最后再将每个通道的卷积结果进行矩阵加法以得到最终的特征图

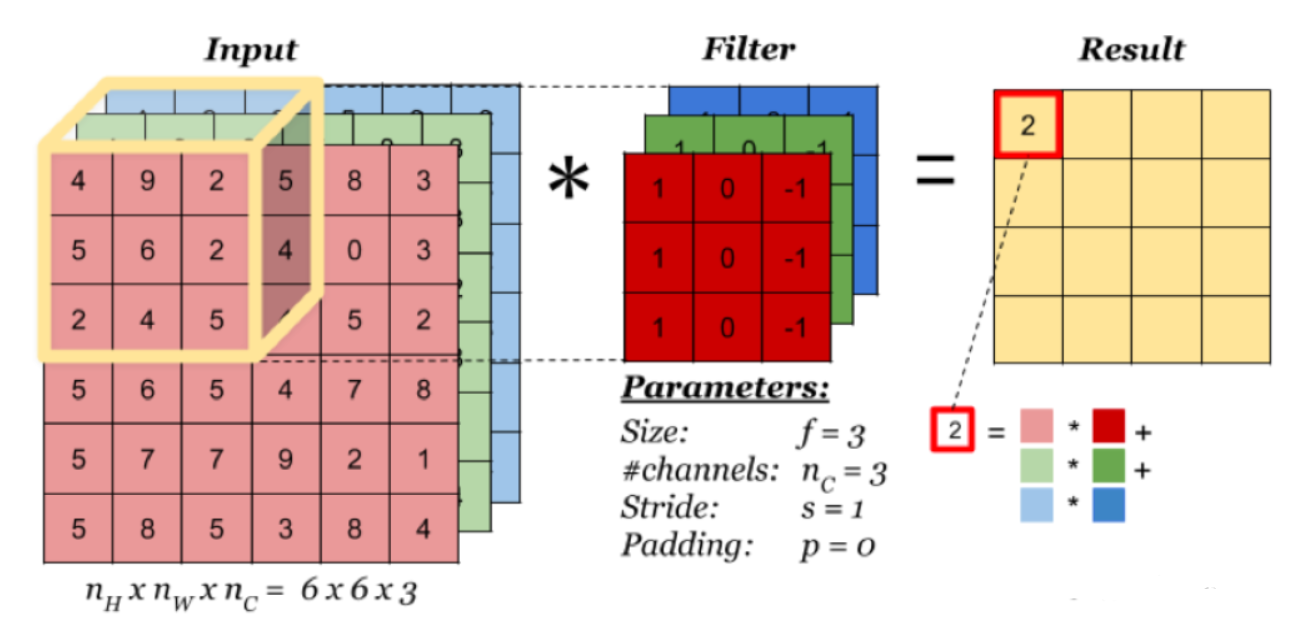
一些检测特定特征的滤波器很容易想到，例如水平滤波器，垂直滤波器等，但能直观想到的滤波器数量有限，CNN 可以自动学习滤波器，调整滤波器里的参数，让计算机自己去理解图像所需的滤波器来检测特征

【多滤波器】

当有多个滤波器时，可以学习到多种不同的特征，对应产生包含多个通道的特征图

如下图所示，存在两个滤波器，每个滤波器学习到一个特征图，每个特征图作为一个通道，因此最终的输出是双通道

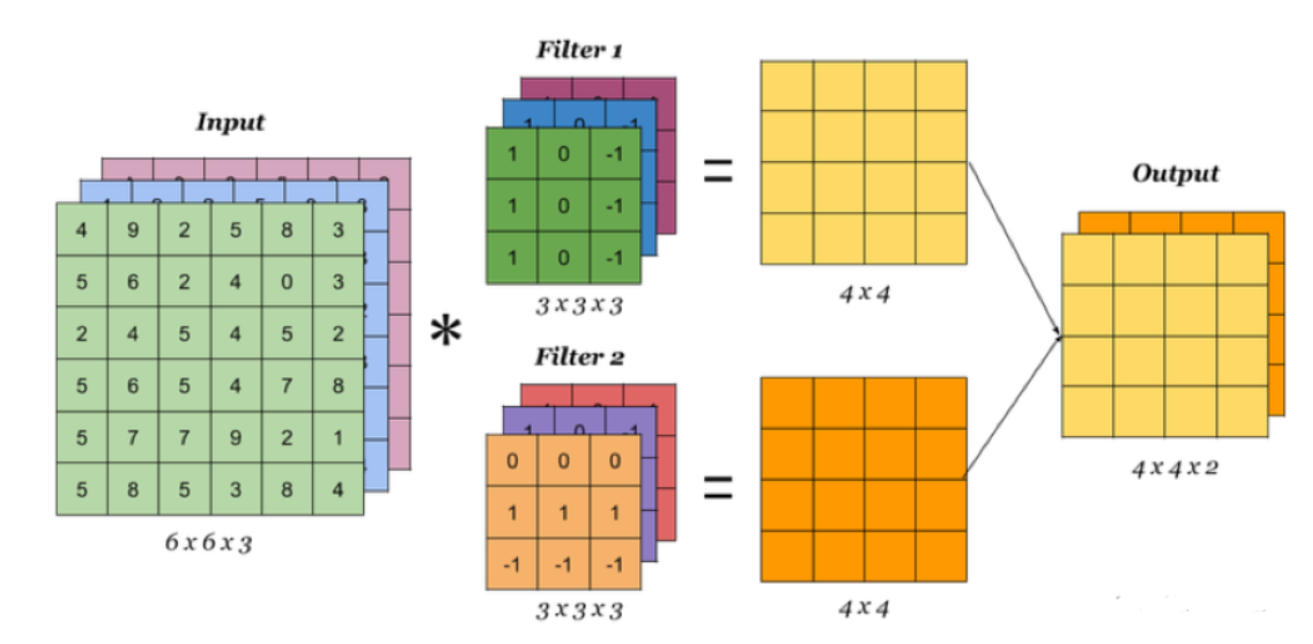
简单来说，对于滤波器的通道数以及输出特征图的通道数，有：

• 某一层滤波器的通道数 = 上一层特征图的通道数
• 某一层输出特征图的通道数 = 当前层滤波器的个数