卷积神经网络的反向传播

Reference：

• 一文入门卷积神经网络：CNN通俗解析
• 卷积神经网络（CNN）详解
• 深度学习系列6：卷积神经网络的反向传播
• 反向传播之六：CNN 卷积层反向传播
• 卷积神经网络(CNN)反向传播算法推导
• Convolutional Neural Networks backpropagation: from intuition to derivation

【概述】

如下图所示，卷积神经网络由若干个卷积层和池化层进行局部特征识别和降维，之后再利用生成的特征图用全连接层去处理

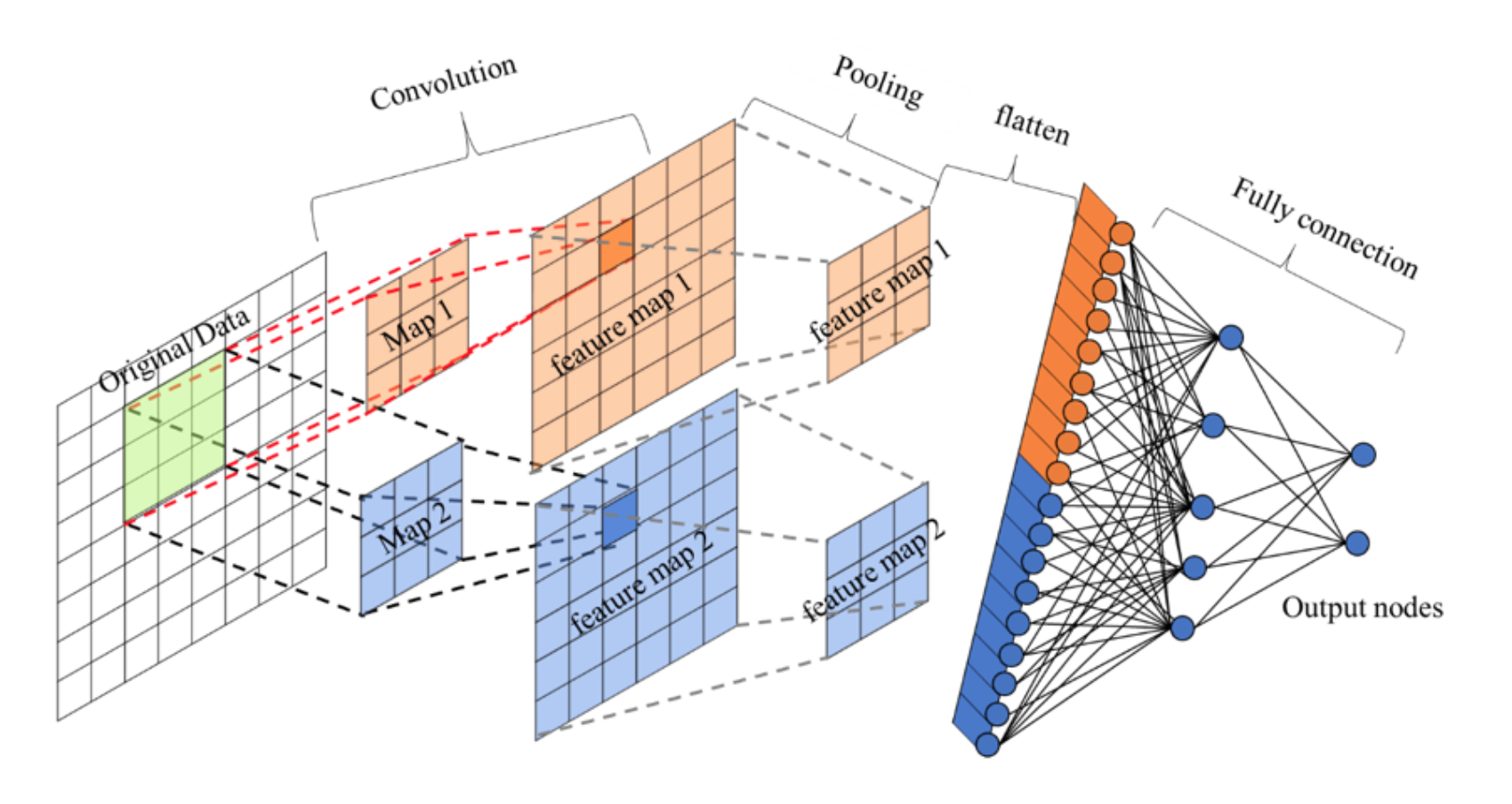
因此，可以将卷积神经网络的反向传播过程分为两个阶段：

1. 对于全连接层，按照 BP 神经网络中的反向传播方式逐层计算
2. 对于卷积层-池化层，按照卷积与池化的反向传播逐层计算

【全连接层】

在 CNN 的全连接层中，反向传播与任何常规的全连接神经网络完全相同，即对于全连接层，有梯度下降方程：

$$\begin{gather*} w_{ij}^{[l]} = w_{ij}^{[l]}-\alpha \cdot \delta_j^{[l+1]} a_i^{[l]} \\ b_{i}^{[l]} = b_{i}^{[l]}-\alpha \cdot \delta_i^{[l+1]} \\ \end{gather*}$$

其中，$\alpha$ 为学习率，$\delta_{j}^{[l]}$ 为第 $L_l$ 层第 $j$ 个神经元的误差，有：

$$\begin{gather*} \delta_{j}^{[l]} = \sum\limits_{k=1}^{S_{l+1}} \bigg[ \delta_k^{[l+1]} \cdot w_{jk}^{[l]} \cdot f'(z_j^{[l]}) \bigg], & l=n_l-1,n_l-2,\cdots,3,2\\ \delta_j^{[n_l]}=\Big[ f(z_j^{[n_l]})-y^{(j)} \Big]\cdot f'(z_j^{[n_l]}), & l=n_l \end{gather*}$$

关于具体的推导过程，详见：BP 神经网络与反向传播算法

【池化层】

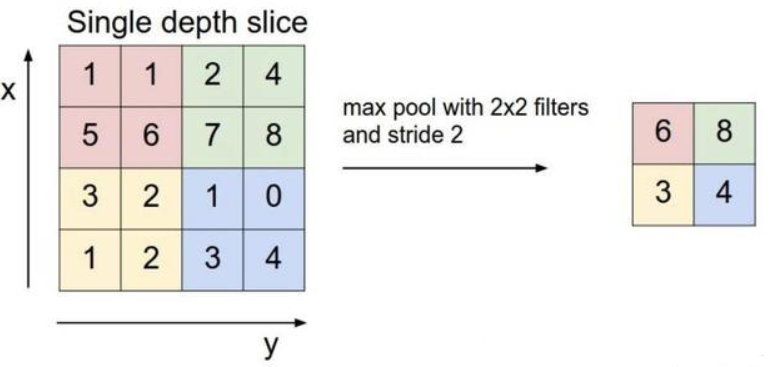
最大池化

在前向传播过程中，最大池化是取每个池化窗口区域的最大值，也就是说，在最大池化层中，梯度仅通过最大值来进行反向传播

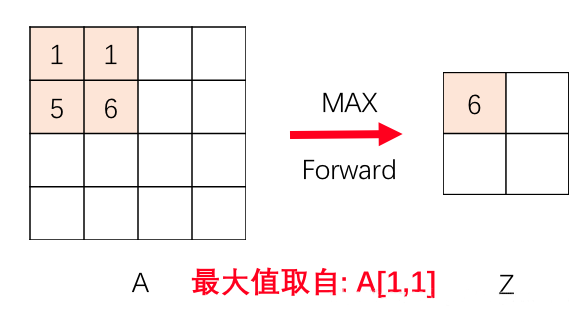
如下图所示，假设最大池化后数字 $6$ 的位置误差为 $\delta$ ，那么误差反向传播回去时，红色区域中最大值对应的位置误差即等于 $\delta$，而其它 $3$ 个位置对应的误差为 $0$

因此，为计算反向传播，在 CNN 进行最大池化前向传播时，不仅要记录区域的最大值，还需要记录最大值 $\max$ 在哪个位置上取得

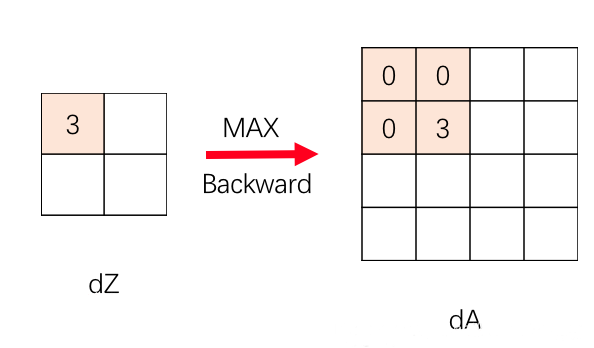
之后，在通过 $dZ^{[l]}$ 计算 $dA^{[l]}$ 时，只需将每个 $dZ^{[l]}$ 的元素对应到 $dA^{[l]}$ 的相应区域，然后令取最大值的位置为最大值 $\max$，其他区域为 $0$

平均池化

在前向传播过程中，平均池化是取每个池化窗口区域的平均值，也就是说窗口区域中的每个值对池化后的结果贡献的权重都为区域大小的倒数

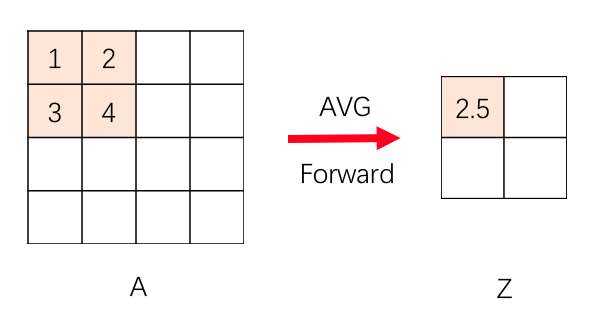
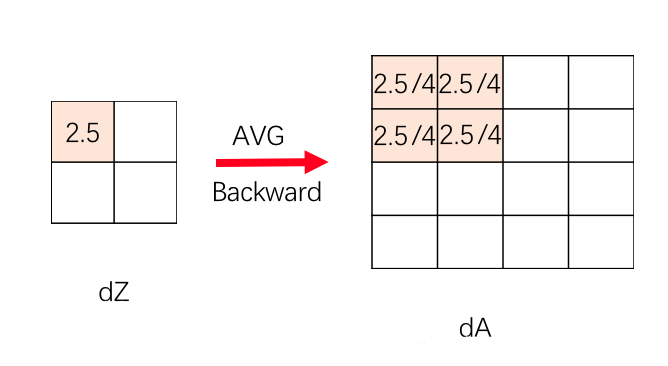
因此，在反向传播时，区域每个位置的误差 $\delta$ 都为池化后误差除以区域的大小，即在通过 计算 $dZ^{[l]}$ 时，只需将每个 $dZ^{[l]}$ 的每个元素均分给对应 $dA^{[l]}$ 的相应区域即可

【卷积层】

卷积层结构

在前向传播时，对于第 $L_l$ 层的卷积层来说，有：

$$Z^{[l]}=W^{[l]} * A^{[l-1]}+\mathbf{b}^{[l]}$$

其中，$*$ 为卷积运算，$W^{[l]}$ 为滤波器

在计算反向传播时，已知 $dZ^{[l]}$，需要求 $dW^{[l]}$、$dA^{[l-1]}$、$d\mathbf{b}^{[l]}$ 即可

$dA^{[l-1]}$ 的计算

在求解 $dA^{[l-1]}$ 时，与偏置向量 $\mathbf{b}^{[l]}$ 无关，因此不需要考虑 $\mathbf{b}^{[l]}$ 的影响

在前向传播过程中，$A^{[l-1]}$ 通过卷积核生成了卷积结果 $Z^{[l]}$，那么在反向传播时，只需要将 $dZ^{[l]}$ 与卷积核进行卷积操作，然后重叠部分叠加即可

如下图所示，前向传播时，$A^{[l-1]}$ 的粉色区域，通过卷积核生成了 $Z^{[l]}$ 的粉色区域 $19$

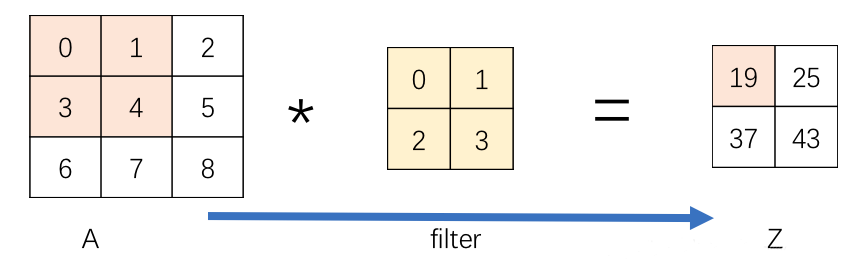
在反向传播时，令 $dA^{[l-1]}$ 的初值为 $0$，然后将已知的 $dZ^{[l]}$ 逐单元与卷积核进行卷积操作，即得到 $dA^{[l-1]}$ 对应位置的值

如下图所示，$dZ^{[l]}$ 的粉色区域 $-1$ 与卷积核相乘，得到 $2\times 2$ 的区域，叠加到 $dA^{[l-1]}$ 相应的粉色区域

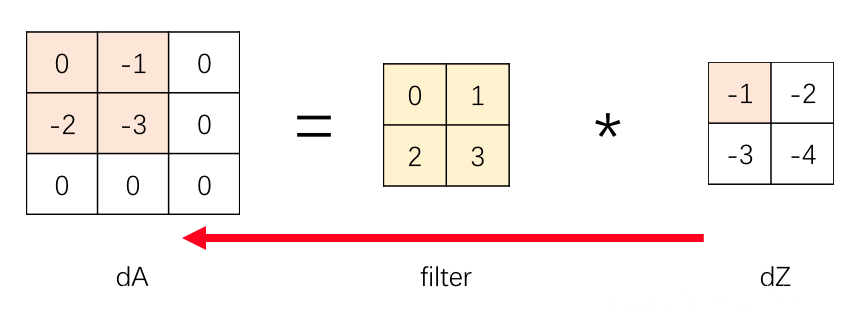
同样，$dZ^{[l]}$ 的蓝色区域 $-2$ 与卷积核相乘，得到 $2\times 2$ 的区域，叠加到 $dA^{[l-1]}$ 相应的蓝色区域

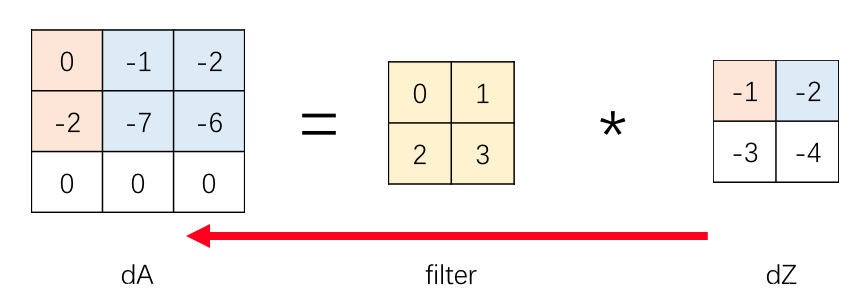
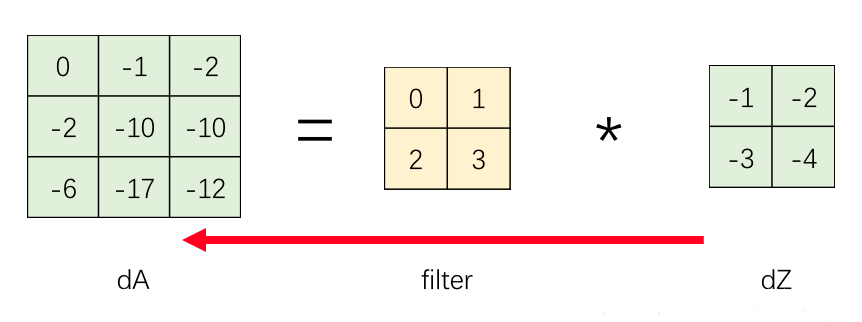
最终，经过对已知的 $dZ^{[l]}$ 的循环，将结果在 $dA^{[l-1]}$ 上叠加，得到最终的 $dA^{[l-1]}$

$dW^{[l]}$ 的计算

在求解 $dW^{[l]}$ 时，与偏置向量 $\mathbf{b}^{[l]}$ 无关，因此不需要考虑 $\mathbf{b}^{[l]}$ 的影响

在反向传播时，令 $dW^{[l]}$ 的初值为 $0$，然后将已知的 $dZ^{[l]}$ 逐单元与 $A^{[l-1]}$ 进行卷积操作，将得到的结果累加到 $dW^{[l]}$ 上，最终对于 $N$ 个样本，还要对 $dW^{[l]}$ 除以样本数 $N$

如下图所示，$A^{[l-1]}$ 的粉色区域与 $dZ^{[l]}$ 对应的粉色区域 $-1$ 相乘，得到 $2\times 2$ 的区域，叠加到 $dW^{[l]}$ 上

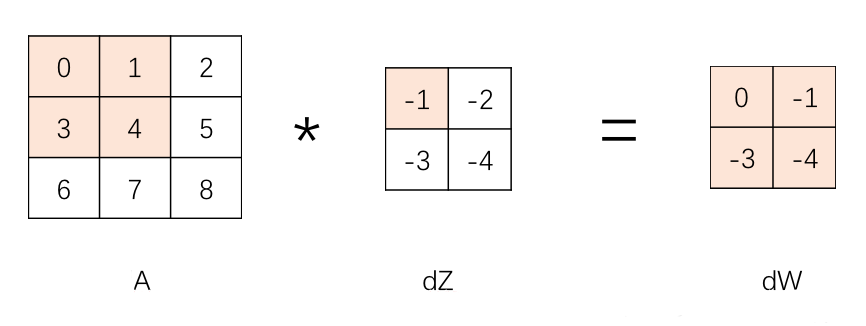
之后，计算 $A^{[l-1]}$ 的蓝色区域 $dZ^{[l]}$ 对应的蓝色区域 $-2$ 的乘积，得到 $2\times 2$ 的区域，叠加到 $dW^{[l]}$ 上

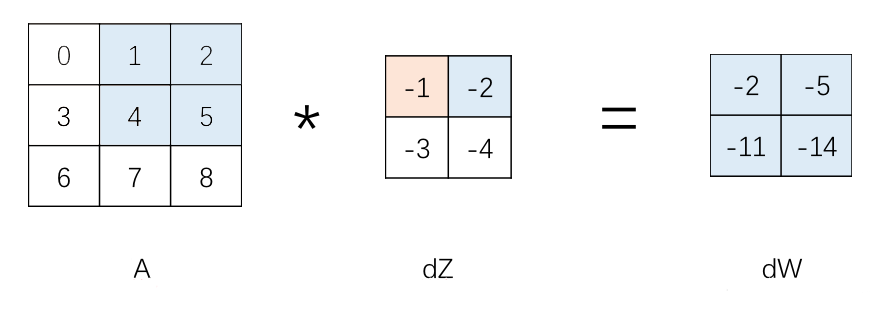
最终，经过对已知的 $dZ^{[l]}$ 的循环，将结果在 $dW^{[l]}$ 上叠加，得到最终的 $dW^{[l]}$

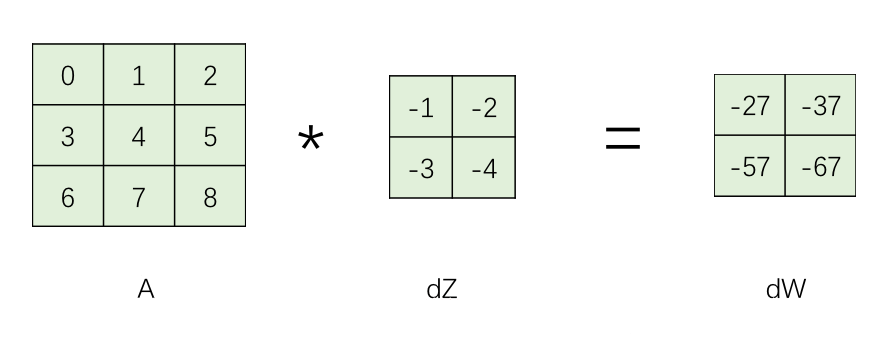
$d\mathbf{b}^{[l]}$ 的计算

$d\mathbf{b}^{[l]}$ 即为已知的 $dZ^{[l]}$ 各元素的累加和

与求解 $dW^{[l]}$ 时相同，最终对于 $N$ 个样本，还要对 $dW^{[l]}$ 除以样本数 $N$