Alex_McAvoy

想要成为渔夫的猎手

图的存储结构

发表于 分类于 ， ，
本文字数： 4.8k 阅读时长 ≈ 4 分钟

【邻接矩阵】

结构

图的邻接矩阵存储也称数组表示法，其方法是用一个一维数组存储图中的顶点，用一个二维数组存储图中的所有的边，存储顶点之间邻接关系的二维数组称为邻接矩阵

设图 $G=(V,E)$ 具有 $n$ 个顶点，则其邻接矩阵是一个 $n*n$ 的方阵，定义为：

若 $G$ 是网图，则有：

其中 $w_{ij}$ 是边 $(v_i,v_j)$ 或弧 $< v_i,v_j >$ 上的权值，$INF$ 代表一极大的数，其大于所有边的权值

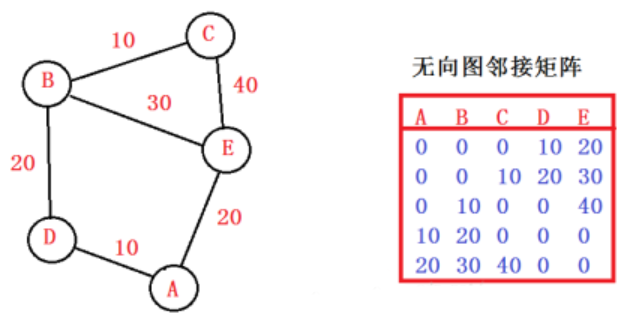
特点

邻接矩阵存储图，其表示方式唯一，具有如下特点：

  • 对于无向图的邻接矩阵，其第 $i$ 行或第 $i$ 列非零元素的个数为第 $i$ 个顶点的度
  • 对于有向图的邻接矩阵，其第 $i$ 行非零元素的个数为第 $i$ 个顶点的出度，第 $i$ 列非零元素的个数为第 $i$ 个顶点的入度
  • 对于图 $G(V,E)$ 的邻接矩阵 $A$，$A^n$ 的元素 $A^n[i][j]$ 为由点 $i$ 到点 $j$ 的长度为 $n$ 的路径的数目
  • 无向图的邻接矩阵是对称矩阵，对于规模大的可以使用压缩存储的方式仅存储上三角或下三角矩阵
  • 邻接矩阵对边的操作效率高，但对于稀疏图来说造成了极大的浪费，因此其只适用于存储点较少的图或稠密图

实现

1
2
3
4
5
6
7
8
9
10
int G[N][N];
void init(int n) {
    memset(G, 0, sizeof(G)); //图的初始化
    while (n--) {
        int x, y, w;
        scanf("%d%d%d", &x, &y, &w); //读入两个顶点序号及权值
        G[x][y] = w;                 //对于不带权的图，可令g[x][y]=1
        G[y][x] = w;                 //无向图的对称性
    }
}

【邻接表】

结构

邻接表是一种顺序存储与链接存储相结合的存储方法，类似于树的孩子链表表示法

对于图 $G$ 的每个顶点 $v_i$，将所有邻接于 $v_i$ 的顶点链成一个单链表，称为 $v_i$ 的边表，第 $i$ 个单链表中的结点表示依附于顶点 $v_i$ 的边，若图 $G$ 是一有向图，则称为 $v_i$ 的出边表

为方便对所有边表的头指针进行存储操作，使用顺序存储，这样，存储边表头指针的数组和存储顶点信息的数组构成了邻接表的表头数组，称为顶点表

顶点表结点由顶点域 pos 和指针域 firstEdge 构成，顶点域存放结点信息（一般为结点编号），指针域指向第一条邻接边的指针

边表结点由位置域 pos、数据域 dis 和指针域 next 构成，pos 指示邻接点（该边附着的另一个结点编号），数据域存放网图的边权，指针域指向下一条邻接边

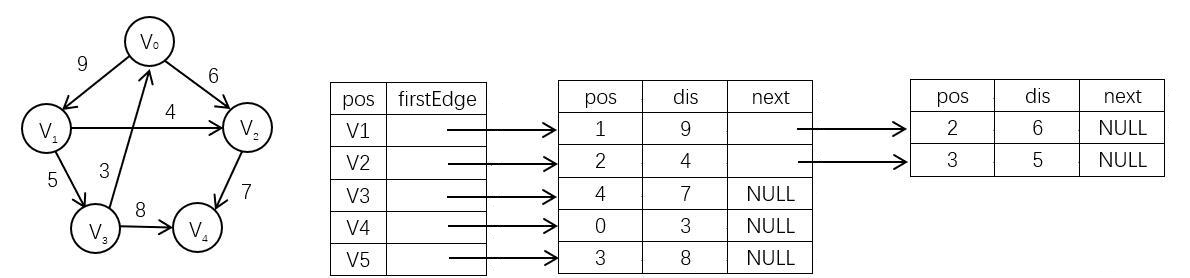
特点

对于邻接表的存储，其表示方式不唯一，具有如下特点：

  • 若 $G(V,E)$ 为无向图，则存储空间为 $O(|V|+2|E|)$
  • 若 $G(V,E)$ 为有向图，则存储空间为 $O(|V|+|E|)$
  • 对于无向图的邻接表，顶点表结点 $i$ 的边表中结点个数为结点 $i$ 的度
  • 对于有向图的邻接表，顶点表结点 $i$ 的边表结点个数为结点 $i$ 的出度，邻接表中所有编号为 $i$ 的边表结点个数为结点 $i$ 的入度
  • 邻接矩阵对点的操作效率高，对于给定的结点，可以轻易的找出其所有邻接边，对不确定的边操作较为方便，可以很好的处理稀疏图

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
struct Edge {   //边表
    int pos;    //位置域，存放该顶点的邻接点在顶点表中的下标
    int dis;    //数据域，对于网图，增设一存取边上信息的域
    Edge *next; //指针域，指向边表中下一结点
};
struct Node {        //顶点表
    int pos;         //顶点域，存放顶点信息
    Edge *firstEdge; //指针域，指向边表中的第一个结点
} node[N];
void init(int n, int m) {
    for (int i = 0; i < n; i++) { //n个点
        scanf("%d", &node[i].pos);
        node[i].firstEdge = NULL;
    }
    for (int i = 0; i < m; i++) { //m条边
        int x, y;
        scanf("%d%d", &x, &y);    //边所依附的两点编号
        Edge *p;                  //边表结点
        //添边x->y
        p->pos = y;
        p->next = node[x].firstEdge;
        node[x].firstEdge = p;
        //添边y->x
        p->pos = x;
        p->next = node[y].firstEdge;
        node[y].firstEdge = p;
    }
}

邻接表与邻接矩阵的转换

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
struct Edge{
    int pos;
    int dis;
    Edge *next;
};
struct Node {
    int pos;
    Edge *firstEdge;
} node[N];   //邻接表
int G[N][N]; //邻接矩阵
int adListToAdMatrix(int n) { //邻接表转邻接矩阵
    for (int i = 0; i < n; i++) { //枚举邻接表中每个点
        Edge *p = node[i].firstEdge;
        while (p != NULL) { //枚举每个点的每条边
            G[i][p->pos] = p->dis;
            p = p->next;
        }
    }
}
void adMatrixToAdList(int n) { //邻接矩阵转邻接表
    for (int i = 0; i < n; i++) //邻接表初始化
        node[i].firstEdge = NULL;
    for (int i = 0; i < n; i++) {
        for (int j = n - 1; j >= 0; j--) {
            if (G[i][j] != 0) { //边存在，头插法建边
                Edge *p = (Edge *)malloc(sizeof(Edge));
                p->pos = j;
                p->next = node[i].firstEdge;
                node[i].firstEdge = p;
            }
        }
    }
}

【前向星与链式前向星】

前向星

对于邻接矩阵来说，其方便但效率低，对于邻接表来说，其虽效率较高但实现较为困难

前向星是一种介于两者之间的较为中庸的结构，虽然好写，但效率较邻接表来说较低，且其不能直接用顶点进行定位，对重边不好处理，只能与邻接表一样遍历判重

前向星借助 STL 中的 vector 容器来储存边的方式来存储图，其通过读入每条边的信息，将边存放在数组中，把数组中的边按照起点顺序排序进行构造

常用于具有多个点或两点间具有多条弧的情况，其缺点是不能直接用顶点进行定位

1
2
3
4
5
6
7
8
9
10
11
int n, m;
vector<int> edge[N];
void init() {
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        int x, y;
        cin >> x >> y; //边所依附的两点编号
        edge[x].push_back(y);//添边x->y
        edge[y].push_back(x);//添边y->x
    }
}

链式前向星

由于借助 vector 实现的前向星的效率并不高，为此借助结构体来模拟链式结构，从而将其进行优化

在优化后，内存利用率高，效率也得到了极大的提升，在常见的图论问题中，链式前向星几乎可适用于所有的图，但其缺点也很明显，如操作复杂化、不好处理重边等

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
struct Edge {
    int next; //下一条边的数组下标
    int to;   //该边的另一个顶点
    int dis;  //该边的权值
} edge[N];
int n, m;     //点数，边数
int head[N];  //head[i]表示顶点i的第一条边的数组下标，-1表示顶点i没有边
int tot;      //边的条数即边序号
void addEdge (int from, int to, int dis) {
    edge[tot].dis = dis; //权值
    edge[tot].to = to;   //另一顶点
    edge[tot].next = head[from];//同结点下该边的下一条边
    head[from] = tot++;  //结点from的第一条边
}
int mian() {
    memset(head, -1, sizeof(head));
    tot = 0;
    
    for (int i = 0; i < m; i++) {
        int x, y, w;
        scanf("%d%d%d", &x, &y, &w);
        addEdge(x, y, w); //添边x->y
        addEdge(y, x, w); //添边y->x
    }
    
    //遍历从x出发的所有边
    int x = 0;
    for (int i = head[x]; i != -1; i = edge[i].next) {
        int y = edge[i].to;
        ...
    }
    ...
    return 0;
}

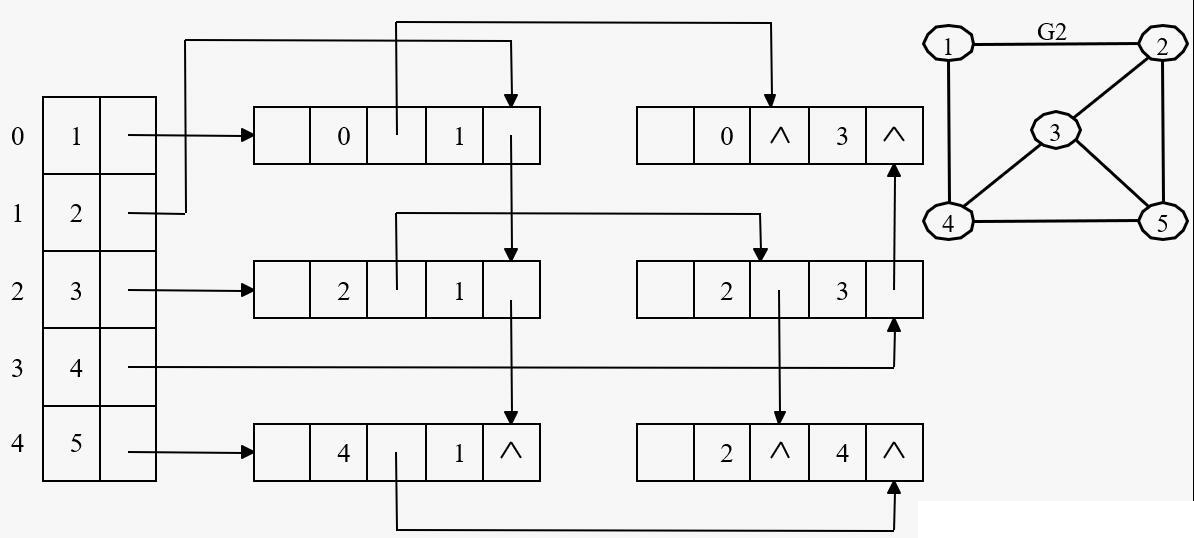
【十字链表与邻接多重表】

十字链表与邻接多重表也是图的一种存储方法，但由于操作复杂、内存利用率不高等因素常不被使用

十字链表

十字链表是有向图的一种存储方法，其实质上是邻接表与逆邻接表的结合

顶点表结点由数据域 data ，入边表头指针firstIn ，出边表头指针 firstOut 构成， 其中， 数据域存放顶点信息（一般为点编号），入边表头指针指向以该顶点为终点的弧构成的链表中的第一个结点；出边表头指针指向以该顶点为始点的弧构成的链表中的第一个结点

边表结点由数据域 data、尾域tailPos 、头域 headPost、入边表指针域headLink、出边表指针域tailLink，其中数据域存放网图的边权，尾域为弧的起点在顶点表中的下标，头域为弧的终点在顶点表中的下标，入边表指针域指向终点相同的下一条边，出边表指针域指向起点相同的下一条边

headLink 为入边表指针域，指向终点相同的下一条边；tailLink 为出边表指针域，指向起点相同的下一条边

邻接多重表

邻接多重表是无向图的一种存储方法，在用邻接表存储无向图时，每条边的两个顶点分别在以该边所依附的两个顶点的边表中，这种重复存储给图的某些操作带来不便，在其基础上有了邻接多重表，两者的差别仅在于同一条边在邻接表用两个结点表示，在邻接多重表用一个结点表示

顶点表结点由数据域 data、边表头指针 firstEdge 构成，其中数据域存放顶点信息（一般为结点编号），边表头指针指向第一条依附于该点的边

边表结点由数据域 data、标志域 mark 、位置域 iPos 与 jPos、位置指针域 iLink与 jLink 构成，其中数据域存放网图的边权，标志域用于标记该边是否被搜索过，位置域分别为某边依附的两结点在顶点表中的下标，位置指针域分别指向依附于结点 iPos 与 jPos 的下一条边

感谢您对我的支持，让我继续努力分享有用的技术与知识点！