【结构】

二叉排序树（Binary Sort Tree，BST），又称二叉搜索树（Binary Search Tree），属于数据结构中的一类，在需要经常进行查找的情景中，该数据结构常被使用，在一般情况下，查询效率比链表结构要高

二叉排序树或是一棵空树，或是一棵具有以下性质的二叉树：

若左子树非空，则左子树上的所有结点值均小于根结点值
若右子树非空，则右子树上的所有结点值均大于根结点值
左、右子树分别也是一棵二叉排序树

根据上述定义可以看出，对于二叉排序树来说，左子树结点值 $<$ 根结点值 $<$ 右子树结点值

因此，当对二叉排序树进行中序遍历时，可以得到一个递增的有序序列

值得注意的是，在二叉排序树中，要求任意两个结点值不相同

【查找】

二叉排序树的查找，是从根结点开始，沿着某个分支逐渐向下比较的过程

如果二叉排序树非空，那么先将给定元素 elem 与根结点 root 的值比较，具体过程如下：

若 elem == root->data，查找成功
若 elem < root->data，在 root 的左子树上进行查找
若 elem > root->data，在 root 的右子树上进行查找

上述过程一直持续到 elem 被找到或者待查找的子树为空，若待查找的子树为空，则查找失败

值得注意的是，当查找失败时，恰好找到了以 elem 为键值的新结点在二叉排序树中的插入位置

BSTNode *searchBST(BSTree root, int elem) { //查找elem所在结点
    if (root == NULL)
        return NULL;
    if (root->data == elem)
        return root;
    if (elem < root->data)
        return searchBST(root->lchild, elem);
    if (elem > root->data)
        return searchBST(root->rchild, elem);
}

【插入】

二叉排序树是一种动态树表，其树的结构通常不是一次生成的，而是在查找过程中，发现不存在相应结点时，进行插入的

向二叉排序树中插入一个元素 elem 的过程如下：

若 root 是空树，则将 elem 作为根节点插入
若 elem == root->data，则插入失败
若 elem < root->data，则将 elem 插入到 root 的左子树中
若 elem > root->data，则将 elem 插入到 root 的右子树中

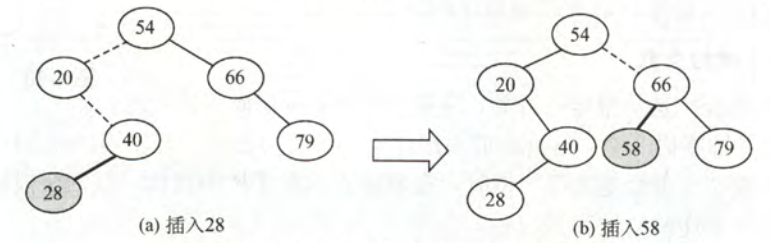
如上图，在图中依次插入结点 $28$ 和 $58$，可以看出，插入的结点是作为叶结点插入到二叉排序树中的

bool insertBST(BSTree &root, int elem) { //插入elem
    if (root == NULL) {
        root = (BSTree)malloc(sizeof(BSTNode));
        root->data = elem;
        root->lchild = NULL;
        root->rchild = NULL;
        return true;
    }
    if (elem == root->data)
        return false;
    if (elem < root->data)
        insertBST(root->lchild, elem);
    if (elem > root->data)
        insertBST(root->rchild, elem);
}

【构造】

从一棵空树出发，依次输入元素，将它们插入二叉排序树中的合适位置，本质上，就是不断将元素插入到二叉排序树中

void creatBST(BSTree &root, int elems[], int n) { //构造二叉排序树
    root = NULL;
    for (int i = 0; i < n; i++)
        insertBST(root, elems[i]);
}

【删除】

在二叉排序中，在删除一个结点时，由于删除的可能是叶结点，也有可能是分支结点，因此在删除时，需要重新修改指针，使得在删除结点后，仍能保持二叉排序树的特性

对于二叉排序树的删除操作，可以分为以下三种情况来处理：

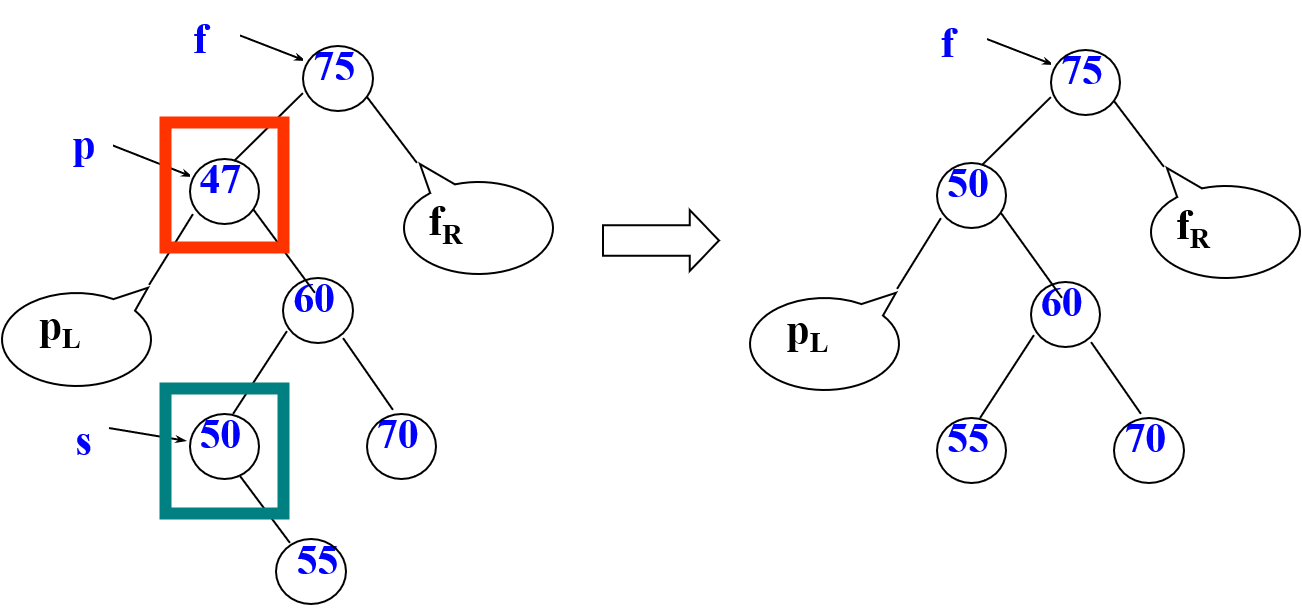
1）待删除结点为叶结点

如下图，待删除结点 p 为叶结点，可以直接将结点 p 的父结点的相应指针域改为空即可，即有：f->lchild

2）待删除结点只有一棵左子树或右子树

如下图，待删除结点 p 只有一棵左子树 pl 或右子树 pr 时，将子树替换为待删除结点 p 的父结点 f 的子树即可，即有：f->lchild = p->lchild 或 f->rchild = p-rchild

3）待删除结点既有左子树又有右子树

如下图，待删除结点 p 既有左子树 pl 又有右子树 pr，那么就寻找该二叉排序树的中序序列中 p 的直接后继或直接前驱来替换结点 p

然后再从树中删除这个被替换的结点，从而将删除情况转换成了情况 1）或情况 2）

void deleteBST(BSTree p, BSTree f) { //删除结点p
    if (p->lchild == NULL && p->rchild == NULL) { // p是叶结点
        if (f->lchild == p) // p是f的左孩子
            f->lchild = NULL;
        else // p是f的右孩子
            f->rchild = NULL;
        free(p);
        return;
    }
    if (p->rchild == NULL) { // p只有左子树
        if (f->lchild == p)  // p是f的左孩子
            f->lchild = p->lchild;
        else  // p是f的右孩子
            f->rchild = p->lchild;
        free(p);
        return;
    }
    if (p->lchild == NULL) { // p只有右子树
        if (f->lchild == p)  // p是f的左孩子
            f->lchild=p->rchild;
        else  // p是f的右孩子
            f->rchild=p->rchild;
        free(p);
        return;
    }
    if (p->lchild != NULL && p->rchild != NULL) { //p左右子树均不空
        f=p;
        BSTNode *s=p->rchild;
        while (s->lchild != NULL) { //查找最左下结点
            f=s;
            s=s->lchild;
        }
        p->data=s->data;
        if (f == p) //特殊情况
            p->rchild=s->rchild;
        else //一般情况
            f->lchild=s->rchild;
        free(p);
        return;
    }
}

【判定】

对于二叉排序树来说，其中序遍历序列为一递增有序序列

因此，对于给定的二叉树进行中序遍历，若其始终能保持前一个值比后一个值小，则说明该二叉树为一个二叉排序树

//调用时，pre初值为-0x3f3f3f3f
bool judge(BSTree root, int pre) { //二叉排序树判定
    if (root == NULL)
        return true;
    bool lflag = judge(root->lchild, pre); //判左子树
    if (!lflag)                            //左子树不是
        return false;
    if (root->data <= pre) //当前结点小于其前驱
        return false;
    pre = root->data;
    bool rflag = judge(root->rchild, pre); //判右子树
    return rflag;
}

【最大最小关键字】

最大关键字

在一棵二叉排序树中，最右下结点即为关键字最大的结点

int getMaxKey(BSTree root) { //求最大关键字
    if (root == NULL)
        return -1;
    while (root->rchild != NULL)
        root = root->rchild;
    return root->data;
}

最小关键字

在一棵二叉排序树中，最左下结点即为关键字最小的结点

int getMinKey(BSTree root) { //求最小关键字
    if (root == NULL)
        return -1;
    while (root->lchild != NULL)
        root = root->lchild;
    return root->data;
}

【查找效率分析】

时间复杂度

二叉排序树的查找效率与二叉排序树的高度有关

在最坏情况下，构造二叉排序树的输入序列是有序的，会形成一个斜树，此时树的高度为 $n$，时间复杂度为 $O(n)$

从查找过程来看，二叉排序树的查找与二分查找类似，但二分查找判定树唯一，则二叉排序树不唯一，这是因为相同关键字插入顺序的不同，可能会生成不同的二叉排序树

就维护表的有序性而言，二叉排序树无须移动结点，仅需修改指针即可完成插入与删除操作，时间复杂度为 $O(log_2n)$

平均查找长度

对于二叉排序树，其查找成功的 $ASL$ 为第 $i$ 个结点的层数和除以结点总个数

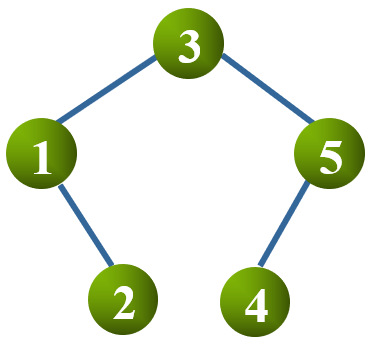
如上图，由序列 $\{3, 1, 2, 5, 4\}$ 构造的二叉排序树，有：

$ASL_{成功}=\frac{1+2+2+3+3}{5}=2.2$

Alex_McAvoy

二叉排序树 BST