【结构】
结构
二叉树排序树 BST 的查找效率取决于二叉排序树的形态,而构造一棵形态均匀的二叉排序树与结点的插入次序有关,但结点的插入次序不是随人的意志决定的,这就要求找到一种动态平衡的方法,对于任意给定的关键码序列都能构造一棵形态均匀、平衡的二叉排序树,这种二叉排序树被称为平衡二叉树(Balance Binary Tree)
平衡二叉树最早由 G. M. Adelson-Velsky 和 E. M. Landis 提出,因此,平衡二叉树常称为 AVL 树
AVL 树其或是一棵空的二叉排序树,或是满足如下性质的二叉排序树:
- 根结点的左子树和右子树深度最多差 $1$
- 根结点的左子树和右子树也是平衡二叉树

平衡因子与最小平衡子树
将平衡二叉树中某个结点的左右子树的深度之差称为平衡因子(Balance Factor),根据平衡二叉树的定义,平衡因子只可能取值 $-1,0,1$
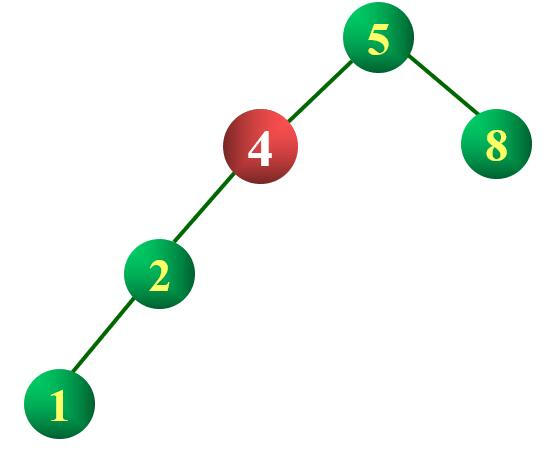
在平衡二叉树构造过程中,以距离插入结点最近的、平衡因子绝对值大于 $1$ 的结点为根的子树,称为最小不平衡子树(Minimal Unbalance Subtree)
【构造】
基本思想
构造平衡二叉树的基本思想是:在构造二叉排序树的过程中,每插入一个结点时,首先检查是否因结点插入而破坏了树的平衡性,若破坏了平衡性,则找出最小不平衡子树,在保持二叉排序树的特性前提下,调整最小不平衡子树中各结点的位置,进行相应旋转,使其成为新的平衡子树
设结点 $A$ 为最小平衡子树的根结点,对该子树进行平衡调整归纳起来有以下四种情况:
- LL 型:右单旋转,顺时针旋转一次
- RR 型:左单旋转,逆时针旋转一次
- LR 型:先左后右双旋转,逆时针旋转一次,再顺时针旋转一次
- RL 型:先有后左双旋转,顺时针选择一次,再逆时针旋转一次
在旋转时,规定旋转优先,即在以某结点为支撑点旋转时,令旋转方向一侧的子树不动
- 顺时针旋转时,旋转前为右子树,旋转后仍为右子树
- 逆时针旋转时,旋转前为左子树,旋转后仍为左子树
LL 型
当新插入的结点,是插在结点 $A$ 的左孩子的左子树上,即为 LL 型
设结点 $B$ 是结点 $A$ 的左孩子,$B_L$、$B_R$ 分别为结点 $B$ 的左右子树,$A_R$ 为结点 $A$ 的右子树,且 $B_L$、$B_R$、$A_R$ 三棵子树的深度均为 $h$
此时,将结点 $X$ 插入到结点 $B$ 的左子树 $B_L$ 上,导致结点 $A$ 的平衡因子由 $1$ 变为 $2$,从而使得以结点 $A$ 为根的子树失去了平衡
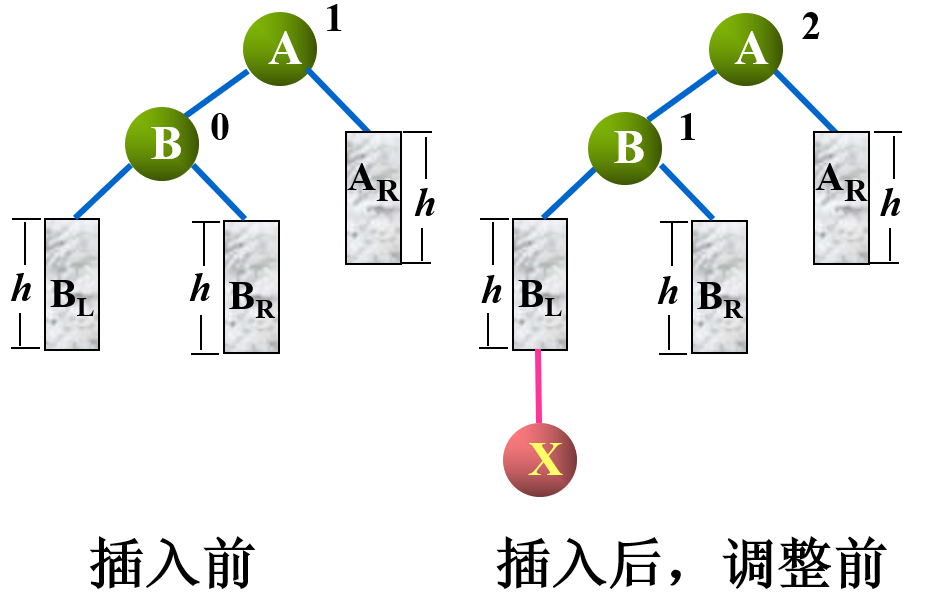
为了使树保持平衡,将支撑点由 $A$ 改为 $B$,相应的进行顺时针旋转,旋转后,结点 $A$ 及其右子树 $A_R$ 和结点 $B$ 的右子树 $B_R$ 发生冲突
根据旋转优先原则,即令结点 $A$ 成为 $B$ 的右孩子结点,结点 $B$ 的右子树 $B_R$ 成为结点 $A$ 的左子树

RR 型
当新插入的结点,是插在结点 $A$ 的右孩子的右子树上,即为 RR 型
设结点 $B$ 是结点 $A$ 的右子树的根结点,$B_L$、$B_R$ 分别为结点 $B$ 的左右子树,$A_L$ 为结点 $A$ 的左子树,且 $B_L$、$B_R$、$A_R$ 三棵子树的深度均为 $h$
此时,将结点 $X$ 插入到结点 $B$ 的右子树 $B_R$ 上,导致结点 $A$ 的平衡因子由 $-1$ 变为 $-2$,使得以结点 $A$ 为根的子树失去了平衡

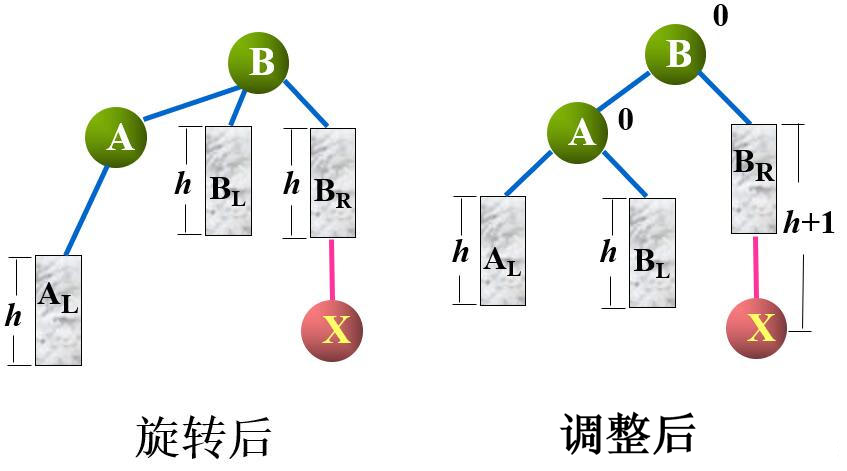
为了使树保持平衡,将支撑点由 $A$ 改为 $B$,相应的进行逆时针旋转,旋转后,结点 $A$ 及其左子树 $A_L$ 和结点 $B$ 的左子树 $B_L$ 发生冲突
根据旋转优先原则,结点 $A$ 成为 $B$ 的左孩子结点,结点 $B$ 的左子树 $B_L$ 成为结点 $A$ 的右子树
LR 型
当新插入的结点,是插在结点 $A$ 的左孩子的右子树上,即为 LR 型
设结点 $B$ 是结点 $A$ 的左子树的根结点,结点 $C$ 是结点 $B$ 的右子树的根节点,$A_R$ 为结点 $A$ 的右子树,$B_L$ 为结点 $B$ 的左子树,$C_L$、$C_R$ 分别为结点 $C$ 的左右子树,且 $B_L$、$A_R$ 两棵子树的深度为 $h$,$C_L$、$C_R$ 两棵子树的深度为 $h-1$
此时,将结点 $x$ 插入到结点 $C$ 的左子树 $C_L$ 上,导致结点 $A$ 的平衡因子由 $1$ 变为 $2$,使得以结点 $A$ 为根的子树失去了平衡
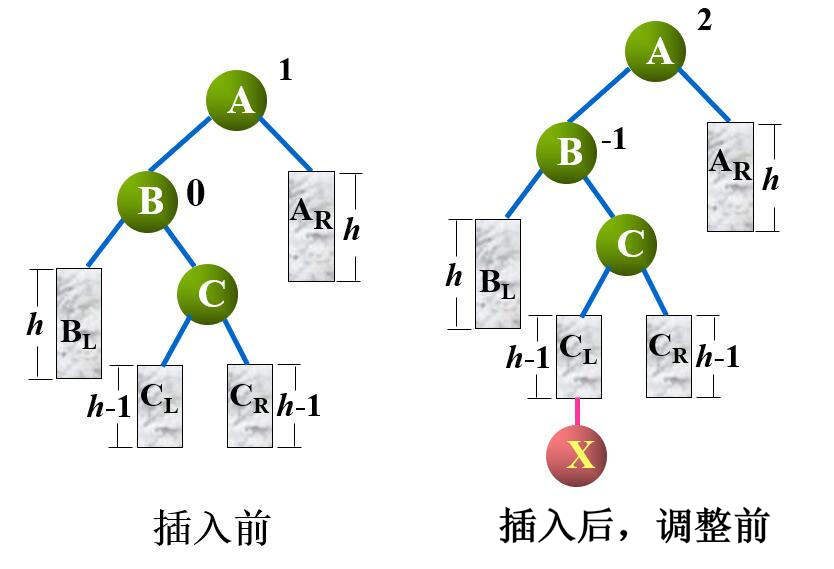
为了使树保持平衡,需要旋转两次:
第一次旋转时,令根节点 $A$ 不动,调整结点 $A$ 的左子树,将支撑点由结点 $B$ 调整到结点 $C$ 处,相应的进行逆时针旋转,旋转后,结点 $B$ 及其左子树与结点 $C$ 的左子树 $C_L$ 发生冲突,按旋转优先原则,结点 $C$ 的左子树成为 $B$ 的右子树

第二次旋转时,将支撑点由结点 $A$ 调整到结点 $C$, 相应的进行顺时针旋转,旋转后,结点 $A$ 及其右子树 $A_R$ 与结点 $C$ 的右子树 $C_R$ 发生冲突,按旋转优先原则,结点 $C$ 的右子树成为结点 $A$ 的左子树

RL 型
当新插入的结点,是插在结点 $A$ 的右孩子的左子树上,即为 RL 型
设结点 $B$ 是结点 $A$ 的右子树的根结点,结点 $C$ 是结点 $B$ 的左子树的根节点,$A_L$ 为结点 $A$ 的左子树,$B_R$ 为结点 $B$ 的右子树,$C_L$、$C_R$ 分别为结点 $C$ 的左右子树,且 $B_R$、$A_L$ 两棵子树的深度为 $h$,$C_L$、$C_R$ 两棵子树的深度为 $h-1$
将结点 $x$ 插入到结点 $C$ 的右子树 $C_R$ 上,导致结点 $A$ 的平衡因子由 $-1$ 变为 $-2$,使得以结点 $A$ 为根的子树失去了平衡

为了使树保持平衡,需要旋转两次:
第一次旋转时,令根节点 $A$ 不动,调整结点 $A$ 的右子树,将支撑点由结点 $B$ 调整到结点 $C$ 处,相应的进行顺时针旋转,旋转后,结点 $B$ 及其右子树与结点 $C$ 的右子树 $C_R$ 发生冲突,按旋转优先原则,结点 $C$ 的右子树成为 $B$ 的左子树
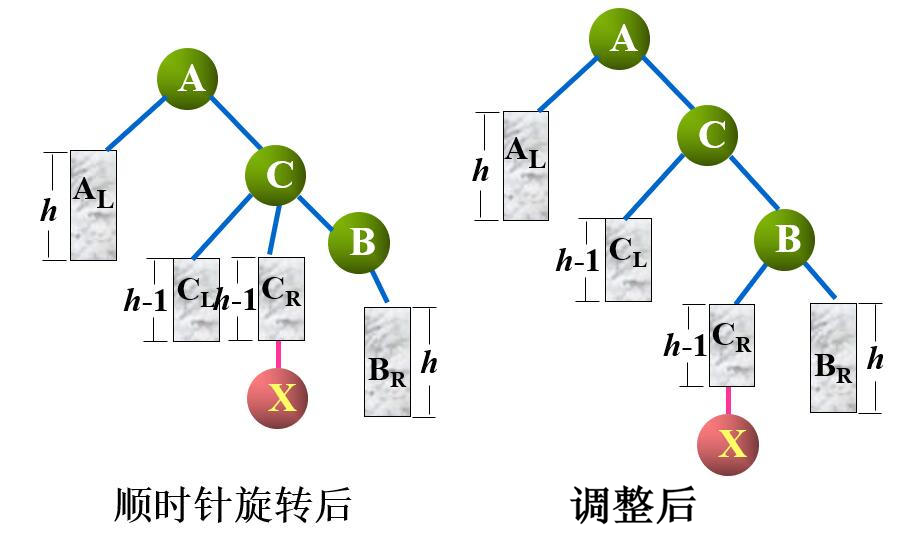
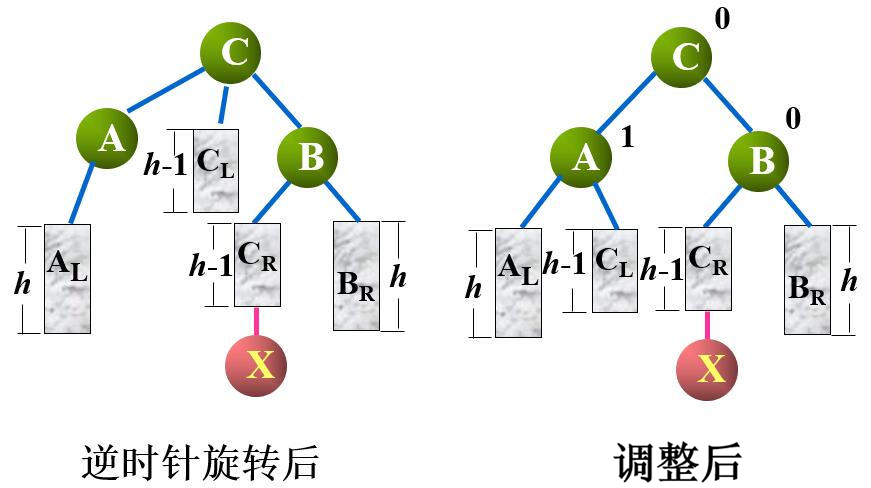
第二次旋转时,将支撑点由结点 $A$ 调整到结点 $C$, 相应的进行逆时针旋转,旋转后,结点 $A$ 及其左子树 $A_R$ 与结点 $C$ 的左子树 $C_L$ 发生冲突,按旋转优先原则,结点 $C$ 的左子树成为结点 $A$ 的右子树
【查找】
在平衡二叉树上进行查找的过程与二叉排序树相同,因此,在查找过程中,与给定值比较的关键字的个数不超过树的深度
假设以 $n_h$ 表示深度为 $h$ 的平衡树中含有的最少结点数(平衡因子为 $1$),则有如下递推公式:
那么,含 $n$ 个结点的平衡二叉树的最大深度为 $O(log_2n)$


