【函数依赖】
函数依赖
设 $R(U)$ 是属性集 $U$ 上的关系模式,$X$、$Y$ 是 $U$ 的子集,若对于 $R(U)$ 的任意一个可能的关系 $r$,$r$ 中不可能存在两个元组在 $X$ 上的属性值相等,而 $Y$ 上的属性值不等,则称 $X$ 函数确定 $Y$,或 $Y$ 函数依赖于 $X$,记作:$X\rightarrow Y$
需要指出的是:
1.函数依赖不是指关系模式 $R$ 的某个或某些关系满足的约束条件,而是指 $R$ 的一切关系均要满足的约束条件,即所有的关系实例均要满足
2.函数依赖与其他的数据依赖均是语义范畴的概念,即只能根据语义来确定一个函数依赖,例如:姓名 $\rightarrow$ 年龄这个函数依赖只能在没有同名人的情况下成立
3.数据库设计者可以对现实世界作强制性规定,例如:规定不允许有同名人出现,从而使得姓名 $\rightarrow$ 年龄这个函数依赖成立,这样当插入某个元组时发现有同名人,则拒绝插入该元组
平凡与非平凡函数依赖
在关系模式 $R(U)$ 中,对于 $U$ 的子集 $X$、$Y$:
如果 $X\rightarrow Y$,但 $Y \subseteq X$,则称 $X\rightarrow Y$ 是平凡的函数依赖
如果 $X\rightarrow Y$,但 $Y \nsubseteq X$,则称 $X\rightarrow Y$ 是非平凡的函数依赖
例如,在关系 SC(Sno, Cno, Grade) 中,(Sno, Cno) → Sno 和 (Sno, Cno) → Cno 是平凡函数依赖,(Sno, Cno) → Grade 是非平凡的函数依赖
对于任一关系模式,平凡函数依赖都是必然成立的,其不反映新的语义,因此,若不特别声明,讨论的总是非平凡函数依赖
完全与部分函数依赖
在介绍完全函数依赖与部分函数依赖前,先给出以下几个定义:
若 $X\rightarrow Y$ ,则 $X$ 称为这个函数依赖的决定属性组,也称为决定因素
若 $X\rightarrow Y$ 且 $Y\rightarrow X$,则记作:$X\leftarrow\rightarrow Y$
若 $Y$ 不依赖于 $X$,则记作:$X\nrightarrow Y$
在 $R(U)$ 中,如果 $X\rightarrow Y$,且对于 $X$ 的任何一个真子集 $X’$,都有 $X’ \nrightarrow Y$,则称 $Y$ 对 $X$ 完全函数依赖,记作:$X\xrightarrow{F}Y$
若 $X\rightarrow Y$,但 $Y$ 不完全函数依赖于 $X$,则称 $Y$ 对 $X$ 部分函数依赖,记作:$X\xrightarrow{P}Y$
例如,在关系 SC(Sno, Cno, Grade, Sdept) 中,(Sno, Cno) → Grade 是完全函数依赖,(Sno, Cno) → Sdept 是部分函数依赖,因为 Sno → Sdept 成立,而 Sno 是 (Sno, Cno) 的真子集
直接与传递函数依赖
在 $R(U)$ 中,如果满、$X\leftarrow\rightarrow Y$、$Y\rightarrow Z$ 则称 $Z$ 对 $X$ 直接函数依赖,记为:$X\xrightarrow{直接}Y$
在 $R(U)$ 中,如果满足 $X\rightarrow Y$、$Y\nrightarrow X$、$Y\rightarrow Z$,则称 $Z$ 对 $X$ 传递函数依赖,记为:$X\xrightarrow{传递}Y$
例如,在关系 SC(Sno, Cno, Grade, Sdept, Mname) 中,有 Sno → Sdept ,Sdept → Mname 成立,故有传递函数依赖 Sno → Mname
属性间联系决定函数依赖关系
假如 $X$、$Y$ 有 $1:1$ 关系,则:$X\rightarrow Y$ 且 $Y\rightarrow X$,可表示为 $X\leftarrow\rightarrow Y$
假如 $X$、$Y$ 有 $1:m$ 关系,则:$Y\rightarrow X$,但 $X\nrightarrow Y$
假如 $X$、$Y$ 有 $n:m$ 关系,则:$X$、$Y$ 不存在任何函数依赖
【多值依赖】
引入
对于 1NF、2NF、3NF、BCNF 来说,都是在函数依赖的范畴内进行讨论,但 BCNF 并非十分完美(关于范式:点击这里)
如下例,学校中某一门课程由多个教师教授,使用相同的参考书,每个教师可以讲授多门课程,每种参考书可以供多门课程使用,可以用一个非规范化的关系来表示教师 T、课程 C、参考书 B 间的关系
可以将这个关系以非规范化的形式列出,如下表
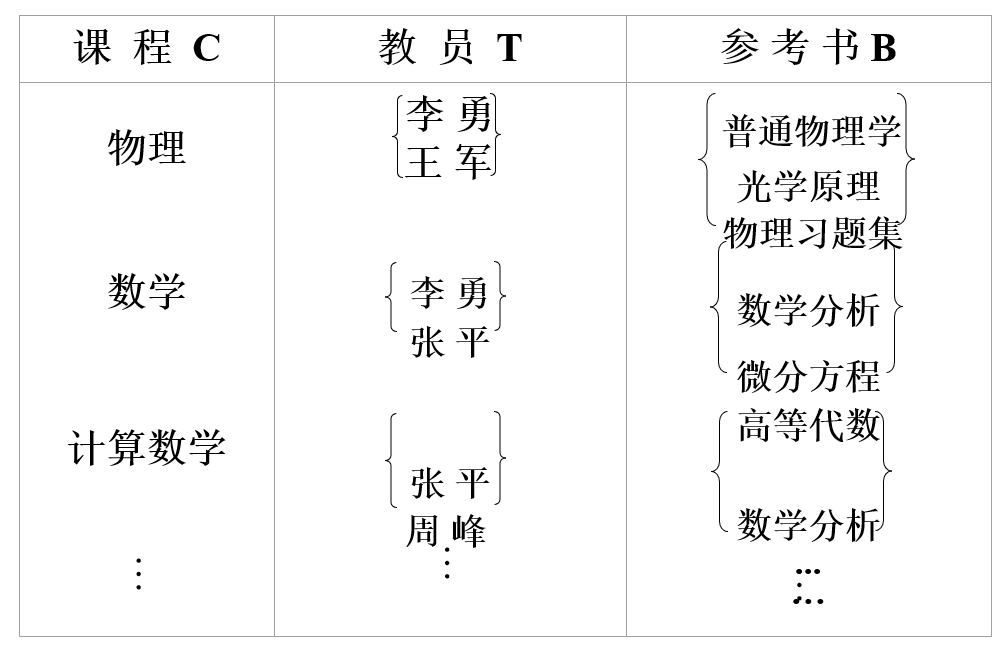
可以发现,关系模式 teaching(C, T, B) 的码 $(C, T, B)$ 是全键(All-Key),其属于 BCNF,将其转为规范化的二维表,如下
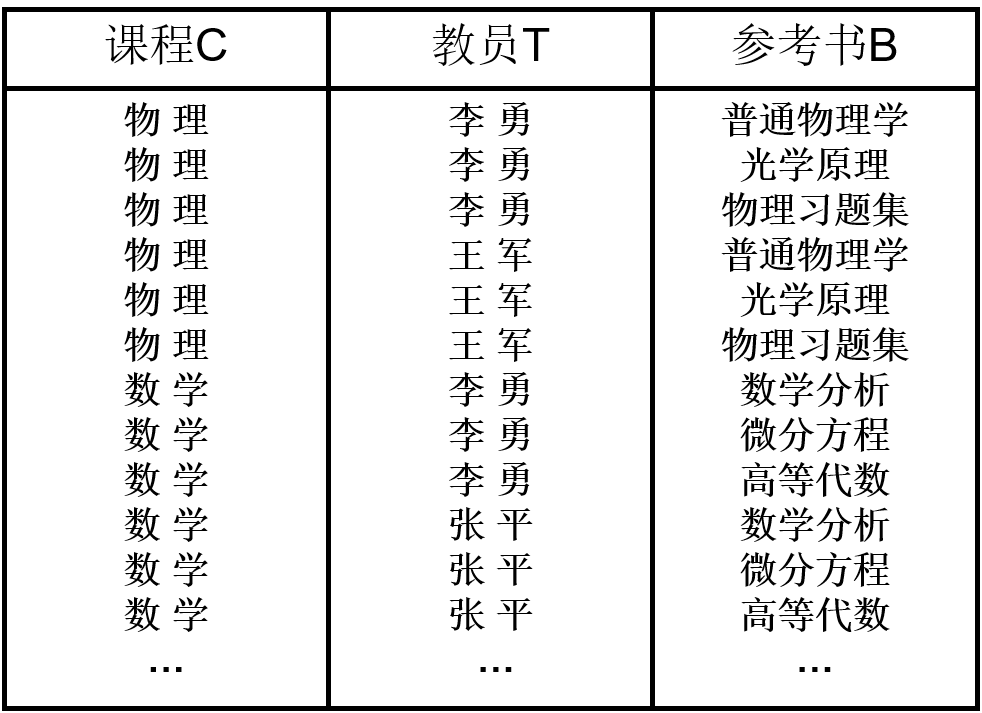
当某一课程增加一名教师时,必须插入多个元组,例如:物理课程添加一名讲课老师张三时,要插入三个元组 (物理, 张三, 普通物理学)、(物理, 张三, 光学原理)、(物理, 张三, 物理习题集)
这对数据的增删改十分不方便,数据的冗余性也十分明显,考察这类的关系模式,发现其具有一种称为多值依赖的数据依赖
多值依赖
设 $R(U)$ 是属性集 $U$ 上的一个关系模式,$X$、$Y$、$Z$ 是 $U$ 的子集,且 $Z=U-X-Y$,当且仅当满足对 $R(U)$ 的任一关系 $r$,给定一对 $(x,z)$ 值,有一组 $y$ 值,且这组值仅决定于 $x$ 值而与 $z$ 值无关时 ,关系模式 $R(U)$ 中多值依赖成立,记作:$X\rightarrow\rightarrow Y$
例如,在关系模式 teaching(C, T, B) 中,对于一个 (物理, 光学原理) 有一组 $T$ 值 {李勇, 王军},这组值仅决定于课程 $C$ 上的值,即对于另一组值 (物理, 普通物理学) 来说,尽管此时参考书 $B$ 的值已经改变,但其对应的一组 $T$ 值仍为 {李勇, 王军},因此 $T$ 多值依赖于 $C$,即:$C\rightarrow\rightarrow T$
平凡与非平凡多值依赖
若 $X\rightarrow\rightarrow Y$,而 $Z=\phi$,即 $Z$ 为空,则称 $X\rightarrow\rightarrow Y$ 为平凡的多值依赖
若 $X\rightarrow\rightarrow Y$,而 $Z\neq \phi$,即 $Z$ 不为空,则称 $X\rightarrow\rightarrow Y$ 为非平凡的多值依赖
一般来说,常见的多值依赖均为非平凡多值依赖
多值依赖的性质
多值依赖具有以下性质:
1.对称性:若 $X\rightarrow\rightarrow Y$,则 $X\rightarrow\rightarrow Z$,其中 $Z=U-X-Y$
2.传递性:若 $X\rightarrow\rightarrow Y$,$Y\rightarrow\rightarrow Z$,则 $X\rightarrow\rightarrow Z-Y$
3.函数依赖是多值依赖的特殊情况:若 $X\rightarrow Y$,则 $X\rightarrow\rightarrow Y$
4.若 $X\rightarrow\rightarrow Y$ 且 $X\rightarrow\rightarrow Z$,则 $X\rightarrow\rightarrow Y\cup Z$
5.若 $X\rightarrow\rightarrow Y$ 且 $X\rightarrow\rightarrow Z$,则 $X\rightarrow\rightarrow Y\cap Z$
6.若 $X\rightarrow\rightarrow Y$ 且 $X\rightarrow\rightarrow Z$,则 $X\rightarrow\rightarrow Y-Z$ 且 $X\rightarrow\rightarrow Z-Y$
【函数依赖与多值依赖的关系】
函数依赖是多值依赖的特殊情况,即当 $X\rightarrow Y$ 时,有 $X\rightarrow\rightarrow Y$,这是因为,当 $X\rightarrow Y$ 时,对 $X$ 的每个值 $x$,$Y$ 都有一个确定值 $y$ 与其对应
但多值依赖与函数依赖相比,有以下两个区别:
1.多值依赖的有效性与属性集范围有关若 $X\rightarrow\rightarrow Y$ 在 $U$ 上成立,则在 $W(XY\subseteq W\subseteq U)$上一定成立
反之不然,即若 $X\rightarrow\rightarrow Y$ 在 $W(XY\subseteq W\subseteq U)$上成立,则在 $U$ 上不一定成立
这是因为多值依赖的定义中不仅涉及属性组 $X$ 和 $Y$,还涉及 $U$ 中其余属性 $Z$
一般地,在 $R(U)$ 上若有 $X\rightarrow\rightarrow Y$ 在 $W(W\subset U)$ 上成立,则称 $X\rightarrow\rightarrow Y$ 为 $R(U)$ 的嵌入型多值依赖
2.多值依赖的子集不成立性若函数依赖 $X\rightarrow Y$ 在 $R(U)$ 上成立,则对于任何 $Y’\subset Y$ 均有 $X\rightarrow Y$
若多值依赖 $X\rightarrow\rightarrow Y$ 在 $R(U)$ 上成立,无法断言对于任何 $Y’\subset Y$ 有 $X\rightarrow\rightarrow Y$ 成立

