【概述】
对于范式来说,数据依赖和函数依赖下定义的码是必不可缺的前置内容,其详细介绍见下:
关系数据库中的关系是要满足一定条件的,满足不同程度要求的为不同范式,满足最低要求的称为第一范式(1NF),在第一范式中进一步满足要求的称为第二范式(2NF),以此类推,直到第五范式
所谓第几范式,是表示关系的某一种级别,所以常称某一关系模式 $R$ 为第几范式,通常可将范式理解成符合某一级别的关系模式的集合,即 $R$ 属于第几范式,就写为 $R\in xNF$
对于各种范式间的关系有:$5NF\subset 4NF\subset BCNF \subset 3NF \subset 2NF \subset 1NF$
简单来说,各范式的特点如下:
- 1NF:字段是最小的单元,不可再分
- 2NF:满足 1NF,表中字段必须完全依赖于全部主键
- 3NF:满足 2NF,非主键外的所有字段必须互不依赖
- BCNF:满足 3NF,且主属性内部不能有部分依赖、传递依赖
- 4NF:满足 3NF,消除多值依赖
- 5NF(较少探讨):满足 4NF,消除连接依赖
【1NF】
第一范式(1NF)的定义为:若关系模式 $R$ 的每一分量都是不可分割的数据项,则 $R\in 1NF$
如下表,就不符合 1NF 的要求
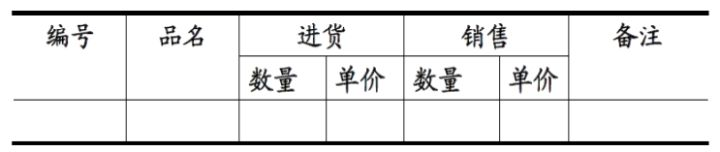
1NF 是所有关系型数据库的最基本要求,在 RDBMS 创建数据表时,如果数据表的设计不符合这个最基本的要求,是无法创建的
也就是说,只要在 RDBMS 中存在的表,一定是满足 1NF 的
如果想要在 RDBMS 中表现出上表中的数据,就要设计成如下表的形式

【2NF】
第二范式(2NF)的定义为:若 $R\in 1NF$ 且每一非主属性完全函数依赖于任何一个候选码,则 $R\in 2NF$
下面举一个不是 $2NF$ 的例子
在关系模式 SLC(Sno, Sdept, Sloc, Cno, Grade) 中,Sloc 为学生的住址(每个系的学生住在一个地方),主码为 (Sno, Cno),那么函数依赖包括:
- $(Sno, Cno)\xrightarrow{F} Grade$
- $Sno\rightarrow Sdept$,$(Sno, Cno)\xrightarrow{P} Sdept$
- $Sno\rightarrow Sloc$,$(Sno, Cno)\xrightarrow{P} Sloc$
- $Sdpt\rightarrow Sloc$
该关系模式中 Sdept、Sloc 部分函数依赖于主码,不符合 $2NF$,其存在如下问题:
- 插入异常:假定插入一个未选课的学生,由于
Cno为NULL,无法插入 - 删除异常:假定某个学生只选了一门课,如果删除了这门课,这个学生的其余信息就丢失了
- 修改困难:假定某个学生选修了 k 门课,
Sdpet、Sloc重复存储了 k 次,要修改一个学生的Sdept时,需要重复修改 $k$ 次 - 数据冗余量大:假定某个学生选修了 k 门课,
Sdpet、Sloc重复存储了 k 次
可以发现,上述例子符合 $1NF$ 但不符合 $2NF$,存在诸多问题,并不是一个好的关系模式
可以利用投影分解法,将这个符合 $1NF$ 但不符合 $2NF$ 的关系模式分解为两个符合 $2NF$ 的关系模式,以一定程度上减轻原来存在的各种异常情况与数据冗余问题
即将关系模式 SLC(Sno, Sdept, Sloc, Cno, Grade) 中部分函数依赖于主码的非主属性 Sdept、Sloc 分解出去,变为两个关系模式 SC(Sno, Cno, Grade) 和 SL(Sno, Sdept, Sloc),其中前者的主码是 (Sno, Cno),后者的主码是 Sno,这样使得非主属性对主码均是完全函数依赖
【3NF】
第三范式(3NF)的定义为:若 $R\in 1NF$ 且 $R$ 中不存在码 $X$、属性组 $Y$、非属性组 $Z\nsubseteq Y$,使得 $X\rightarrow Y$,$Y\rightarrow Z$ 成立,且 $Y\nrightarrow X$,则 $R\in 3NF$
简单来说,$3NF$ 在 $2NF$ 的基础上,消除了非主属性对于码的传递函数依赖,也就是说,如果存在非主属性对于码的传递函数依赖,则不符合 $3NF$ 的要求
如上例,在将关系模式 SLC(Sno, Sdept, Sloc, Cno, Grade) 分解为 SC(Sno, Cno, Grade) 和 SL(Sno, Sdept, Sloc) 后,对于关系模式 SL,其存在函数依赖:
- $Sno\rightarrow Sdept$
- $Sdept\rightarrow Sloc$
在该种情况下,存在非主属性码的函数传递依赖,即:$Sno\xrightarrow{传递} Sloc$,此时出现修改复杂问题,例如:一个系的学生换了宿舍楼
可以发现,将一个 $1NF$ 分解为多个 $2NF$ 后,并不能完全消除关系模式中的异常情况和数据冗余,此时可以利用投影分解法,进一步进行分解,消除传递函数依赖
即将关系模式 SL(Sno, Sdept, Sloc) 分解为两个满足 $3NF$ 的关系模式 SD(Sno, Sdept) 和 DL(Sdept, Sloc)
符合 $3NF$ 要求的数据库设计,基本上解决了数据冗余过大与各种异常问题,在实际应用上,往往为了性能上或者应对扩展的需要,做到 $2NF$ 或者 $1NF$ 即可
【BCNF】
$BCNF$ 比 $3NF$ 更进了一步,通常被认为是修正的第三范式,其定义为:若 $R\in 1NF$ 且 $X\rightarrow Y$ 且 $Y\nsubseteq X$ 时,$X$ 必包含码,则 $R\in BCNF$
简单来说,如果对于一个关系模式 $R$,如果每一个决定属性因素都包含有码,那么 $R\in BCNF$
由 $BCNF$ 的定义可以得到如下结论,即一个满足 $BCNF$ 的关系模式有:
- 所有非主属性对每一个码都是完整函数依赖
- 所有主属性对每一个不包含它的码都是完全函数依赖
- 没有任何属性完全函数依赖于非码的任何一组属性
由于 $R\in BCNF$ 按定义排除了任何属性对码的传递依赖与部分依赖,因此 $R\in 3NF$,但是如果 $R\in 3NF$,未必有 $R\in BCNF$
例如,对于仓库管理关系 WM(Wno, Mno, Ano, Num),其中 Wno 为仓库号,Ino 为物品号,Ano 为管理员号,Num 为物品数量,满足一个管理员仅在一个仓库工作,一个仓库可以存储多种物品,则存在以下关系:
- $(Wno, Ino)\rightarrow (Ano, Num)$
- $(Ano, Num)\rightarrow (Wno, Ino)$
可以发现,$(Wno, Ino)$ 和 $(Ano, Num)$ 都是该关系的候选码,表中唯一非关键字段是数量 Num,这个关系是符合 $3NF$ 的
但由于存在如下关系:
- $Wno \rightarrow Ano$
- $Ano\rightarrow Wno$
即存在关键字段决定关键字段的情况,这是不符合 $BCNF$ 的,此时可以利用投影分解法,进一步进行分解,消除属性对码的依赖
即将关系模式 WM(Wno, Ino, Ano, Num) 分解为两个满足 $BCNF$ 的关系模式 WA(Wno, Ano) 和 WI(Wno, Ino, Num)
【4NF】
第四范式(4NF)的定义为:若关系模式 $R\in 1NF$ 且对于 $R$ 的每个非平凡多值依赖 $X\rightarrow\rightarrow Y (Y\nsubseteq X)$,$X$ 都有码,则 $R\in 4NF$
简单来说,如果 $R\in 4NF$,则:
- 不允许有非平凡且非函数依赖的多值依赖
- 允许有非平凡多字依赖是函数依赖
【如何判断关系 R 是第几范式】
已知一个关系模式的属性之间的语义,也就是相互依赖的关系,如何判断该模式满足第几范式?
1.首先要通过语义把属性之间的函数依赖关系列出来
2.然后确定哪些属性组合可以候选码,从而找出非主属性和主属性
3.然后判断是否存在非主属性与码之间的部分函数依赖关系,如果存在,则不满足 2NF,如不存在部分函数依赖,则属于 2NF
4.继续进行下一步判断,判断非主属性与码之间存在传递依赖关系,不存在,则为 3NF
5.决定因素是否包含码,满足条件则为 BCNF

