【树的遍历】
树中最基本的操作是遍历,从根结点出发,按照某种次序访问树中的所有结点,使得每个结点仅被访问一次
根据树的定义可知:一棵树由根结点和 $m$ 棵子树构成,因此只要递归的遍历根结点和 $m$ 棵子树即可遍历整棵树
树的遍历通常分为三种方式:
- 前序遍历:先访问根结点,再从左到右遍历各棵子树(实质:DFS)
- 后序遍历:先从左到右遍历各棵子树,再访问根结点(实质:DFS)
- 层次遍历:按层次从小到大逐个访问,同一层次按照从左到右的次序(实质:BFS)
从树的孩子兄弟表示法和二叉树的二叉链表表示法可以看出,树的孩子兄弟表示法实质上是二叉树的二叉链表存储形式,因此,从物理结构上来看,两者是相同的,只是解释不同
因此,以二叉链表为媒介,可导出树与二叉树间的对应关系,也就是说,给出一棵树,可以找到一棵唯一的二叉树与之对应,这样一来,对树的操作即可借助二叉树的存储,利用二叉树上的操作实现
根据树与二叉树的转换关系以及二叉树的遍历操作可知:
- 树的前序遍历 $<=>$ 二叉树的前序遍历
- 树的后序遍历 $<=>$ 二叉树的中序遍历
【森林的遍历】
$m(m>=0)$棵互不相交的树的集合称为森林(forest)
森林有两种遍历方法:森林的前序遍历、森林的后序遍历
根据森林与二叉树的转换关系以及二叉树的遍历操作可知:
- 森林的前序遍历 $<=>$ 森林中每棵树的前序遍历 $<=>$ 二叉树的前序遍历
- 森林的后序遍历 $<=>$ 森林中每棵树的后序遍历 $<=>$ 二叉树的中序遍历
【树转二叉树】
将一棵树转为二叉树的方法是:
1)加线:树中所有相邻兄弟结点间加一条线
2)去线:对树中的每个结点,只保留他与第一个子结点的连线,删除与其他子结点的连线
3)层次调整:以根结点为轴心,将树顺时针旋转一定角度,使之层次分明

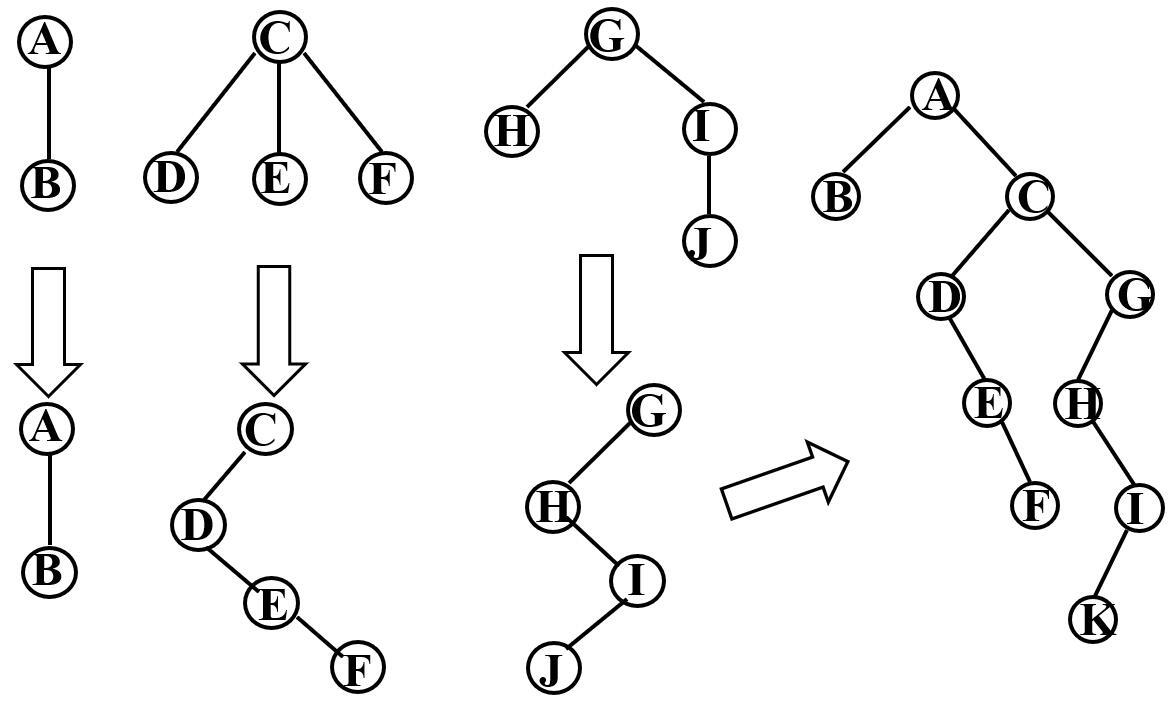
【森林转二叉树】
森林是若干棵树的集合,将森林转成二叉树时,只要先将森林中的每棵树转为二叉树,再将每棵树的根结点视为兄弟即可
将森林转为二叉树的方法是:
1)转树:将森林中的每棵树转换成二叉树
2)连接:从第二棵树二叉树开始,依次将后一棵二叉树的根结点作为前一棵二叉树根结点的右孩子
【二叉树转树或森林】
树和森林都能转成二叉树,二者的不同是树转成的二叉树其根结点无右子树,森林转成的二叉树其根结点有右子树
显然,这一转换过程是可逆的,即:根据二叉树的根结点有无右子树,将其还原成树或森林
将一棵二叉树转成树或森林的方法是:
1)加线:若某结点 $x$ 是其双亲 $y$ 的左孩子,则把结点 $x$ 的右孩子、右孩子的右孩子$…$,都与结点 $y$ 用线连起来
2)去线:删去原二叉树中所有的双亲结点与右孩子结点的连线
3)层次调整:整理 1)、2)步得到的树或森林,使之层次分明


