【定点数的表示】
无符号数与有符号数
计算机中,参与运算的机器数有两类:无符号数、有符号数
- 无符号数:整个机器字长的全部二进制位均为数值位,没有符号位,相当于数的绝对值
- 有符号数:有符号数用 0 表示正号,用 1 表示负号,从而将符号数值化,并通常约定二进制的最高位为符号位,即将符号位放在有效数字的前面
机器数的定点表示
根据小数点的位置是否固定,在计算机中有两种数据格式:定点表示、浮点表示
定点表示即约定机器数中的小数点位置是固定不变的,小数点不再使用 . 表示,而是约定它的位置
理论上,小数点位置固定在哪一位都可以,但在计算机中通常采用两种简单的约定:将小数点的位置固定在数据的最高位之前,或者是固定在最低位之后
一般常称前者为定点小数,后者为定点整数
定点小数
定点小数是纯小数,约定小数点位置在符号位之后、有效数值部分最高位之前
若数据 $X$ 的形式为 $X=x_0x_1x_2…x_n$,则在计算机中的表示形式如下:

当 $x_0=0$,$x_1 \sim x_n$ 均为 $1$时,$X$ 为其所能表示的最大正数,真值等于 $1-2^{-n}”$
当 $x_0=1$,$x_1 \sim x_n$ 均为 $1$时,$X$ 为其所能表示的最小负数,真值等于 $-(1-2^{-n})$
其中,$x_0$ 为符号位,$x_1 \sim x_n$ 是数值的有效部分,称为尾数
定点整数
定点整数是纯整数,约定小数点位置在有效数值部分最低位之后
若数据 $X$ 的形式为 $X=x_0x_1x_2…x_n$,则在计算机中的表示形式如下:

当 $x_0=0$,$x_1 \sim x_n$ 均为 $1$时,$X$ 为其所能表示的最大正数,真值等于 $2^{n}-1”$
当 $x_0=1$,$x_1 \sim x_n$ 均为 $1$时,$X$ 为其所能表示的最小负数,真值等于 $-(2^{n}-1)$
其中,$x_0$ 为符号位,$x_1 \sim x_n$ 是数值的有效部分,称为尾数
符号扩展
在计算机算术运算中,有时必须将采用给定位数表示的数转换成具有不同位数的某种表示形式
例如,某个程序需要将一个 $8$ 位数与另外一个 $32$ 位数相加,要想得到正确的结果,在将 $8$ 位数与 $32$ 位数相加之前,必须将 $8$ 位数转换成 $32$ 位数形式,这称为符号扩展
对于正数来说,将原有形式的符号位移动到新形式的符号位上,新表示形式的所有附加位都用 $0$ 进行填充即可
对于负数来说,其符号扩展方法根据机器数的不同而不同
- 原码:表示负数的符号扩展方法与正数相同,但此时符号位为 $1$
- 补码:原有形式的符号位移动到新形式的符号位上,对于整数,新表示形式的所有附加位都用 $1$ 进行填充,对于小数则用 $0$ 进行填充
- 反码:原有形式的符号位移动到新形式的符号位上,新表示形式的所有附加位都用 $1$ 进行填充
【定点数的运算】
定点数的移位运算
算术移位
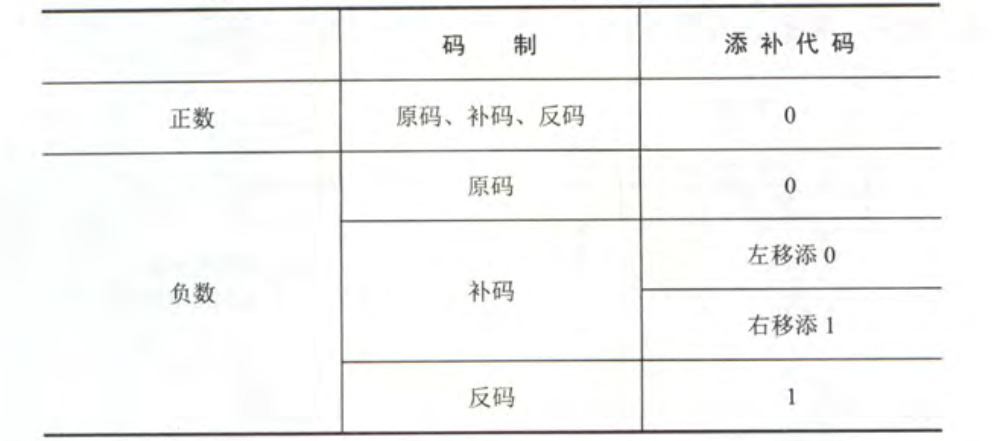
算式移位的对象是带符号数,在移位过程中符号位保持不变
对于正数,由于 $[x]_真 =[x]_原= [x]_补 =[x]_反$,因此移位后出现的空位均添加 $0$
对于负数,由于原码、补码、反码表现形式不同,对移位后出现的空位的添补规则也不同
具体的补位规则见下表
逻辑移位
逻辑移位将操作数当做无符号数看待,具体规则如下:
- 逻辑左移:高位移丢,低位补 $0$
- 逻辑右移:低位移丢,高位补 $0$
循环移位
循环移位操作适用于将数据的低字节数据和高字节数据互换,具体分为带进位标志位 CF 的循环移位(大循环),和不带进位标志位 CF 的循环移位(小循环),其过程如下图所示

原码定点数的加减运算
对于 $[X]_原 = x_s.x_1x_2…x_n$ 和 $[Y]_原 = y_s.y_1y_2…y_n$,在进行加减运算时,规则如下:
- 加法规则:判断符号位,若相同,则绝对值相加,结果符号位不变;若不同,则令绝对值大的数减去绝对值小的数,结果符号位与绝对值大的数相同
- 减法规则:两原码表示的数相减,首先将减数符号取反,然后令被减数与符号取反后的减数进行原码加法计算
补码定点数加减运算
运算规则
由于补码加减运算规则简单,因此在计算机中,多采用补码进行加减运算,其特点如下:
- 参加运算的两操作数均用补码表示
- 按二进制运算规则,逢二进一
- 符号位与数值位按同样规则一起运算,符号位产生的进位要丢弃,结果的符号位由运算得出
- 补码运算的结果亦为补码
具体运算规则如下:
取模运算是为了丢弃溢出位,当参与运算的数是定点小数时,$M=2$,当参与运算的数是定点整数时,$M=2^{n+1}$,$n+1$ 为机器字长
溢出
溢出是指运算结果超过了数的表示范围
通常,称大于机器所能表示的最大正数为上溢,小于机器所能表示的最小负数为下溢
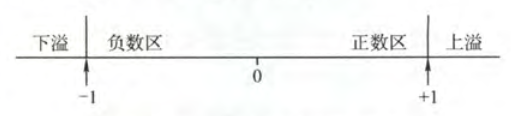
仅当两个符号相同的数相加,或两个符号相异的数相减才可能产生溢出,例如两个正数相加,而结果的符号位却为 $1$,又例如一个负数减去一个正数,结果的符号位却为 $0$
补码定点数加减法运算判断溢出的方式有三种:
1.单符号位判断溢出
由于减法运算在计算机中是用加法器实现的,因此无论是加法还是减法,只要参加操作的两个数符号相同,结果却与原操作数符号不同,就说明结果溢出
设 $A$ 的符号为 $A_s$,$B$ 的符号为 $B_s$,运算结果符号为 $S_s$,则溢出逻辑表达式为:
当 $V=1$ 时,说明结果溢出
2.双符号位判断溢出
双符号位又称模 $4$ 补码,当运算结果的两个符号位相同时,说明未溢出,当运算结果的两个符号位不同时,说明溢出,此时最高位符号位代表真正的符号
对于符号位 $S_{s1}$ 和 $S_{s2}$ 的各种情况如下:
- $S_{s1}S_{s2}=00$:结果为正数,未溢出
- $S_{s1}S_{s2}=01$:出现正溢出
- $S_{s1}S_{s2}=10$:出现负溢出
- $S_{s1}S_{s2}=11$:结果为负数,未溢出
溢出逻辑表达式如下:
当 $V=1$ 时,说明结果溢出
3.单符号位根据进位判断溢出
若符号位的进位 $C_s$ 与最高数位 $C_1$ 相同时,说明未发生溢出
溢出逻辑表达式如下:
当 $V=1$ 时,说明结果溢出

