【原码】
原码是一种简单、直观的机器数表示法,用机器数的最高位表示该数的符号,其余各位表示数的绝对值
纯小数
纯小数的原码定义如下:
如下 $x_1$、$x_2$ 的二进制小数:
字长为 $8$ 位,其原码表示为:
若字长为 $n+1$,则原码小数的表示范围为:
纯整数
纯整数的原码定义如下:
如下 $x_1$、$x_2$ 的二进制整数:
字长为 $8$ 位,其原码表示为:
若字长为 $n+1$,则原码整数的表示范围为:
需要注意的是,在计算机中,真值 $0$ 的原码表示有正零、负零两种形式:
【补码】
原码表示法的加减法操作比较复杂,对于两个不同符号数的加法或同符号数的减法,先要比较两个数的绝对值的大小,然后用绝对值大的数减去绝对值小的数,最后还要结合结果选择合适的符号
而在补码表示法中,加减法则统一采用加法操作即可实现
纯小数
纯小数的补码定义如下:
如下 $x_1$、$x_2$ 的二进制小数:
字长为 $8$ 位,其补码表示为:
若字长为 $n+1$,则补码小数的表示范围为:
纯整数
纯整数的补码定义如下:
如下 $x_1$、$x_2$ 的二进制整数:
字长为 $8$ 位,其补码表示为:
若字长为 $n+1$,则补码整数的表示范围为:
对于正数来说,原码与补码的表示相同,即有:
对于负数来说,原码符号位不变,数值位按位取反,末位加 $1$,即可得到对应的补码;相应的,补码符号位不变,数值位按位取反,末位加 $1$,即可得到对应的原码
【反码】
反码,常用于作为由原码求补码,或者由补码求原码的中间过渡
纯小数
纯小数的反码定义如下:
如下 $x_1$、$x_2$ 的二进制小数:
字长为 $8$ 位,其反码表示为:
若字长为 $n+1$,则反码小数的表示范围为:
纯整数
纯整数的反码定义如下:
如下 $x_1$、$x_2$ 的二进制整数:
字长为 $8$ 位,其反码表示为:
若字长为 $n+1$,则反码整数的表示范围为:
需要注意的是,在计算机中,真值 $0$ 的反码与原码一样,有正零、负零两种形式:
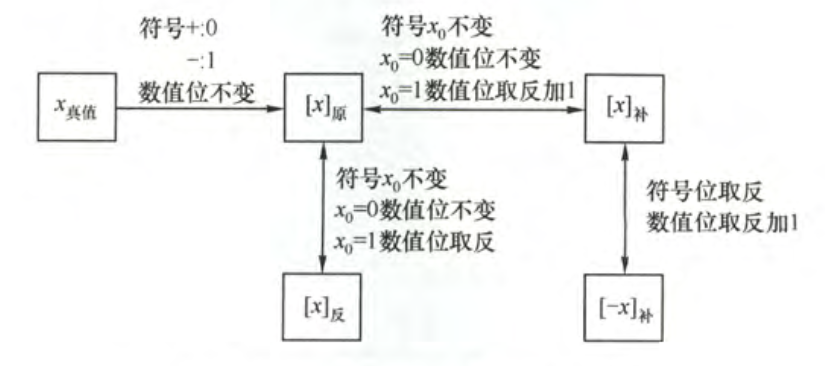
对于真值、原码、补码、反码的转换规律如图所示
【移码】
移码常用于表示浮点数的阶码,其只能表示整数
简单来说,移码就是在真值 $X$ 上加上一个常数作为偏置值,通常这个常数取 $2^n$,相当于 $X$ 在数轴上向正方向偏移了若干单位
移码的定义如下:
如下 $x_1$、$x_2$ 的二进制整数:
字长为 $8$ 位,其移码表示为:
同时,移码具备以下特点:
- 移码中真值 $0$ 的表示唯一,即:$[0]_移=100…0$
- 一个真值的移码与补码仅差一个符号位,即 $[x]_补$ 的符号位取反即可得 $[x]_移$
- 移码全 $0$ 时,对应真值的最小值 $-2^n$;移码全 $1$ 时,对应真值的最大值 $2^n-1$
- 移码保持了数据原有的大小顺序,移码大真值就大,移码小真值就小

