【浮点数表示】
表示格式
通常,浮点数被表示为:
其中,$r$ 是浮点数阶码的底,与尾数的基数相同,通常 $r=2$,$E$、$M$ 是带符号的定点数,$E$ 被称为阶码,$M$ 被称为尾数
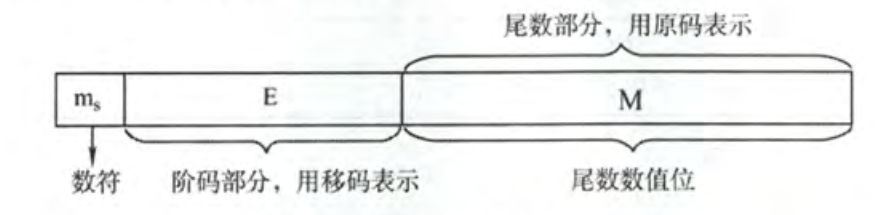
如下图,显示了浮点数的一般格式,阶符 $J_f$ 和阶码的位数 $m$ 合起来反映浮点数的表示范围与小数点的实际位置,数符 $S_f$ 表示浮点数的符号,尾数的位数 $n$ 反映了浮点数的精度

规格化浮点数
规格化操作
为了提高运算的精度,需要充分地利用尾数的有效数位,通常采取浮点数规格化形式,即规定尾数的最高数位必须是一个有效值
非规格化浮点数需要进行规格化操作才能变成规格化浮点数,规格化操作就是通过调整一个非规格化浮点数的尾数和阶码的大小,使非零的浮点数在尾数的最高数位上保证是一个有效值
规格化操作有以下两种:
- 左规:当浮点数运算的结果为非规格化时要进行规格化处理,将尾数算术左移一位,阶码 $-1$ 的
- 右规:当浮点数运算的结果尾数出现溢出(双符号位为 $01$ 或 $10$)时,将尾数算术右移一位,阶码 $+1$
左规可能要进行多次,右规只需进行一次
规格化尾数
在规格化后,规格化浮点数的尾数 $M$ 的绝对值应满足:
在计算机中,常取 $r=2$,故有:
而规格化表示的尾数形式如下:
1.原码规格化
对于正数为 $0.1xx···x$ 的形式,其最大值表示为 $0.11···1$,最小值表示为 $0.100···0$,此时尾数的表示范围为:
对于负数为 $1.1xx···x$的形式,其最大值表示为 $1.10···0$,最小值表示为 $1.11··1$,此时尾数的表示范围为:
2.补码规格化
对于正数为 $0.1xx···x$ 的形式,其最大值表示为 $0.11···1$,最小值表示为 $0.100···0$,此时尾数的表示范围为:
对于负数为 $1.0xx···x$ 的形式,其最大值表示为 $1.01···1$,最小值表示为 $1.00···0$,此时尾数的表示范围为:
需要注意的是,当浮点数尾数的基数为 $2$ 时,原码规格化数的尾数最高位一定是 $1$,补码规格化数的尾数最高位一定与尾数符号位相反
同时,基数不同,浮点数的规格化形式也不同,例如:当基数为 $4$ 时,原码规格化形式的尾数最高两位不全为 $0$;当基数为 $8$ 时,原码规格化形式的尾数最高 $3$ 位不全为 $0$
溢出
当运算结果大于最大正数称为正上溢,小于绝对值最大负数称为负上溢,正上溢和负上溢统称为上溢,数据一旦产生上溢,计算机必须中断运算操作,进行溢出处理
当运算结果在 $0$ 至最小正数之间称为正下溢,在 $0$ 至绝对值最小负数之间称为负下溢,正下溢和负下溢统称为下溢,数据下溢时,浮点数数值趋于 $0$,计算机会将其当作机器零进行处理

IEEE754 标准
IEEE754 标准规定常用的浮点数格式如下
在该标准中,规定常用的浮点数格式有短浮点数(单精度 float 型)、长浮点数(双精度 double 型)、临时浮点数上中年,具体格式要求如下表

对于短浮点数和长浮点数来说,尾数用隐藏位策略的原码表示,阶码用移码表示,故对于真值,有:
- 短浮点数:$(-1)^s \times 1.M \times 2^{E-127}$
- 长浮点数:$(-1)^s \times 1.M \times 2^{E-1023}$
其中,$s=0$ 表示正数,$s=1$ 表示负数;短浮点数 $E$ 为 $8$ 位表示,其取值为 $1 \sim 254$,$M$ 为 $23$ 位,共 $32$ 位;长浮点数 $E$ 的取值为 $11$ 位表示,其取值为 $1\sim 2046$,$M$ 为 $52$ 位 ,共 $64$ 位
综上,IEEE754 标准浮点数范围可见下表:
| 格式 | 最小值 | 最大值 |
|---|---|---|
| 单精度 | $E=1$,$M=0$ $1.0\times 2^{1-127}=2^{-126}$ |
$E=254$,$M=.111…$ $1.111…1\times 2^{254-127}=2^{127}\times (2-2^{-23})$ |
| 双精度 | $E=1$,$M=0$ $1.0\times 2^{1-1023}=2^{-1022}$ |
$E=2046$,$M=.111…$ $1.111…1\times 2^{2046-1023}=2^{1023}\times (2-2^{-52})$ |
【浮点数的加减运算】
步骤
浮点数的加减运算一律采用补码,其特点是阶码运算和尾数运算分开进行,具体步骤如下:
1.对阶
对阶的目的是使两个操作数的小数点位置对齐,即使两个数的阶码相等
对阶的步骤是:先求阶差,然后按小阶向大阶看齐的原则,将阶码小的尾数右移一位,同时阶 $+1$,直到两个数的阶码相等为止
要注意的是,在进行尾数右移时,舍弃掉有效位会产生误差,影响计算精度
2.尾数求和
在对阶后,将对阶的尾数按定点数加减运算规则进行计算
关于定点数加减法的运算规则具体见:定点数的表示与加减运算
3.规格化
以双符号位为例,当尾数大于 $0$ 时,其补码规格化形式为:
当尾数小于 $0$ 时,其补码规格化形式为:
可见,当尾数最高数值位与符号位不同时,即为规格化形式
规格化分为左规和右规两种:
- 左规:当尾数出现 $00.0xx…x$ 或 $11.1xx…x$ 时,需要进行左规,即尾数左移 $1$ 位,和的阶码 $-1$,直到尾数为 $00.1xx…x$ 或 $11.0xx…x$
- 右规:当尾数求和结果溢出,即尾数出现 $10.xx…x$ 或 $01.xx…x$ 的形式时,需要进行右规,即尾数右移 $1$ 位,和的阶码 $+1$
4.舍入
在对阶和右规的过程中,对尾数进行了舍入,这个过程可能会将尾数低位丢失,引起误差,影响精度
常见的舍入方法两种有:
- $0$ 舍 $1$ 入法:类似于十进制数运算中的四舍五入即在尾数右移时,被移去的最高数值位为 $0$,则舍去;被移去的最高数值位为 $1$,则在尾数的末位 $+1$,这样做可能会使尾数又溢出,此时需再做一次右规
- 恒置 $1$ 法:尾数右移时,不论丢掉的最高数值位是 $1$ 还是 $0$,都使右移后的尾数末位恒置 $1$,这种方法可能会使尾数变大,也可能会使尾数变小
5.溢出判断
与定点数加减法一样,浮点数加减运算最后一步也需判断溢出
在浮点数规格化中已指出,当尾数之和或尾数之差出现 $01.xx···x$或 $10.xx···x$ 时,并不表示溢出,只有将此数右规后,再根据阶码来判断浮点数运算结果是否溢出
而浮点数的溢出与否是由阶码的符号决定的,以双符号位补码为例,当阶码的符号位出现 $01$ 时,即阶码大于最大阶码,表示上溢,进入中断处理;当阶码的符号位出现 $10$ 时,即阶码小于最小阶码,表示下溢,按机器零处理
实际原理还是阶码符号位不同表示溢出,且真实符号位和高位符号位一致
实例
设浮点数阶码、尾数用补码表示,采用双符号位,阶码位数为 $5$,尾数位数为 $7$
已知 $x=2^7 \times \frac{29}{32}$,$y=2^5\times \frac{5}{8}$,求 $x+y$
对于 $x$,将其转成二进制形式有:
对于 $y$,将其转成二进制形式有:
首先进行对阶,$x$、$y$ 的阶码相减有:
易得 $x$ 阶码比 $y$ 大 $2$,将 $y$ 的阶码 $+2$,尾数右移 $2$ 位,有:
之后,令对阶后的 $x$、$y$ 的尾数相加,有:
可以发现符号位为 $01$,需要进行右规
令尾数右移一位,阶码 $+1$,有:
此时,阶码符号位为 $01$,可以判断发生上溢,进入中断处理

