【齐次马尔可夫链】
设 $\{X(n),n\geq 0\}$ 为马尔可夫链,若其一步转移概率 $p_{ij}(n)$ 恒与起始时刻 $n$ 无关,则称 $\{X(n),n\geq 0\}$ 为时间齐次的马尔可夫链(Time Homogeneous Markov Chain),简称齐次马尔可夫链
对于齐次马尔可夫链 $\{X(n),n\geq 0\}$,其一步转移概率简记为 $p_{ij}$,其 $k$ 步转移概率 $p_{ij}^{(k)}(n)$ 也恒与起始时刻 $n$ 无关,可记为 $p_{ij}^{(k)}$,因此在进行具体讨论时,总可假设时间起点为零,即
进而其 $k$ 步转移概率矩阵 $P^{(k)}(n)$ 和一步转移概率矩阵 $P(n)$ 也恒与起始时刻 $n$ 无关,简记为 $P^{(k)}$ 和 $P$
【平稳分布】
若 $\{X(n),n\geq 0\}$ 为齐次马尔可夫链,同时是严平稳过程,则称其具有平稳分布
直观上,若马尔可夫链的平稳分布存在,那么以该平稳分布作为初始分布,面向未来进行随机状态转移,之后任何一个时刻的状态分布都是该平稳分布
需要注意的是,马尔可夫链可能存在唯一的平稳分布,也可能有无穷多个平稳分布,甚至不存在平稳分布
平稳分布的形式化定义如下:
设 $\{X(n),n\geq 0\}$ 为马尔可夫链,$P(p_{ij})$ 为转移概率矩阵,若状态空间 $S$ 为离散状态空间上存在一个分布:
使得
则称该分布 $\pi$ 为该马尔可夫链的平稳分布
而对于状态空间 $S$ 为连续状态空间的马尔可夫链来说,对于转移核 $p(x,A)$,若分布 $\pi(x)$ 满足:
则称分布 $\pi(y)$ 为该马尔可夫链的平稳分布,等价地,有:
【平稳分布的获取】
设 $\{X(n),n\geq 0\}$ 为马尔可夫链,$P(p_{ij})$ 为转移概率矩阵,状态空间为 $S$,则分布:
为 $\{X(n),n\geq 0\}$ 的平稳分布的充分必要条件是:$\pi = [\pi_1,\pi_2,\cdots]^T$ 是下列方程组的解
证明:
1)必要性
假设 $\pi=(\pi_1,\pi_2,\cdots)^T$ 是平稳分布,显然满足 $x_j \geq 0$ 与 $\sum\limits_{j} x_j =1$
而
故 $\pi=(\pi_1,\pi_2,\cdots)^T$ 满足 $x_j = \sum\limits_i p_{ij}x_i$
必要性得证
2)充分性
由 $x_j \geq 0$ 与 $\sum\limits_{j} x_j =1$ 可知,$\pi=(\pi_1,\pi_2,\cdots)^T$ 是一概率分布
假设 $\pi=(\pi_1,\pi_2,\cdots)^T$ 为 $X_t$ 的分布,那么对任意 $t\in T$,有:
而 $\pi=(\pi_1,\pi_2,\cdots)^T$ 也是 $X_{t-1}$ 的分布,故:
充分性得证
【实例】
假设有转移概率如下的马尔可夫链
其状态转移图如下所示,求其平稳分布
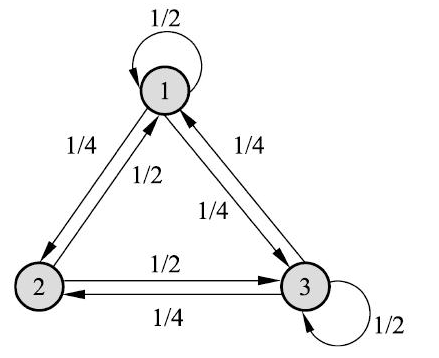
设平稳分布为 $\pi=(x_1,x_2,x_3)^T$,根据方法二中的方程组,有:
解方程组,可得唯一的平稳分布:

