【转移概率与转移概率矩阵】
转移概率
设 $\{X(n),n\geq 0\}$ 为离散时间马尔可夫链 DTMC,当 $X(t)$ 的状态空间 $S$ 为离散状态空间时
若在 $n$ 时刻处于状态 $i$ 的条件下,经过 $k$ 步转移,于 $n+k$ 时刻到达状态 $j$,此时的条件概率
称为 $\{X(n),n\geq 0\}$ 在 $n$ 时刻的 $k$ 步转移概率
特别地,当 $k=1$ 时,$p_{ij}^{(1)}(n)$ 被称为一步转移概率,简记为 $p_{ij}(n)$
转移概率矩阵
将以转移概率 $p_{ij}^{(k)}(n)$ 为第 $i$ 行第 $j$ 列元素组成的矩阵
称为 $\{X(n),n\geq 0\}$ 在 $n$ 时的 $k$ 步转移概率矩阵,其是一个随机矩阵(Stochastic Matrix),即满足:
特别地,当 $k=1$ 时,$P^{(1)}(n)$ 被称为一步转移概率矩阵,简记为 $P(n)$
【C-K 方程】
设 $\{X(n),n\geq 0\}$ 为离散时间马尔可夫链 DTMC,当 $X(t)$ 的状态空间 $S$ 为离散状态空间时
若在 $n$ 时刻处于状态 $i$ 的条件下,经过 $k+m$ 步转移,于 $n+k+m$ 时刻到达状态 $j$,可以先在 $n$ 时从状态 $i$ 出发,经过 $k$ 步于 $n+k$ 时到达某种中间状态 $l$,再在 $n+k$ 时刻从中间状态 $l$ 出发,经过 $m$ 步转移于 $n+k+m$ 时刻到达最终状态 $j$,要求中间状态 $l$ 要取遍整个状态空间,即:
其矩阵形式为:
当取 $m=1$ 时,有
一直推下去,有
写成分量形式,即
在上式中将 $k+1$ 换为 $k$,可得结论:马尔可夫链的 $k$ 步转移概率,由一步转移概率所完全确定
【概率分布】
设 $\{X(n),n\geq 0\}$ 为离散时间马尔可夫链 DTMC,当 $X(t)$ 的状态空间 $S$ 为离散状态空间时,称:
为 $\{X(n),n\geq 0\}$ 在 $n$ 时刻状态为 $i$ 的状态分布,称:
为 $\{X(n),n\geq 0\}$ 在 $n$ 时刻的状态分布向量
特别地,当时刻 $n=0$ 时,称:
为 $\{X(n),n\geq 0\}$ 的初始分布,称:
为 $\{X(n),n\geq 0\}$ 的初始分布向量
显然,状态分布、初始分布、$n$ 步转移概率有如下关系:
【转移概率与转移核】
设 $\{X(n),n\geq 0\}$ 为离散时间马尔可夫链 DTMC,当 $X(t)$ 的状态空间 $S$ 为连续状态空间时,转移概率分布由转移核(Transition Kernel)表示
对任意的 $x\in S,A\subset S$,转移核 $P(x,A)$ 定义为:
其中,$p(x,\cdot)$ 为概率密度函数,满足:
转移核 $P(x,A)$ 表示 $x\sim A$ 的转移概率,即对 $\forall n\geq 2,\forall t_{n-1}<t_n\in T$,有:
【实例】
下面通过一个简单的例子给出马尔可夫链的直观解释
假设观察某地的天气,按日依次是“晴,雨,晴,晴,晴,雨,晴······”,天气的变化具有马尔可夫性,即明天的天气只依赖于今天的天气,而与昨天及以前的天气无关
- 若今天是晴天,那么明天是晴天的概率是 $0.9$,是雨天的概率是 $0.1$
- 若今天是雨天,那么明天是晴天的概率是 $0.5$,是雨天的概率是 $0.5$
状态转移图如下所示
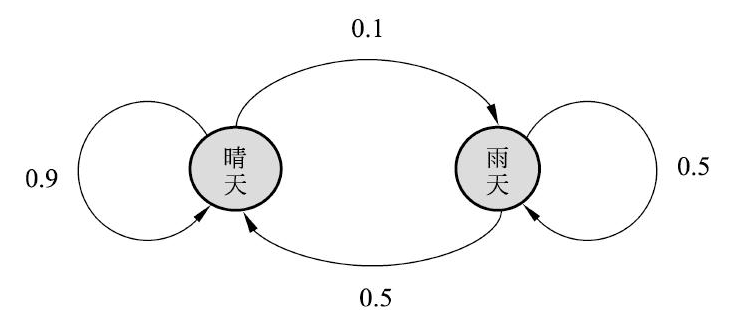
根据如上所示的马尔可夫链的状态转移图,可得转移矩阵为:
如果第一天是晴天的话,其天气概率分布即初始状态分布向量,有:
根据转移矩阵和初始状态,可以计算出第二天、第三天以及之后的天气概率分布,即状态分布向量,有:

