【状态的基本属性】

首达概率与迟早概率

设马尔可夫链 $\{X_n,n\geq0\}$，当 $i,j\in S$，称：

$f_{ij}^{(n)}=P(X_n=j,X_k\neq j,k=1,2,\cdots,n-1|X_0=i)$

为 $\{X_n,n\geq0\}$ 在 $0$ 时刻从状态 $i$ 出发，经过 $n$ 步转移后，首次达到状态 $j$ 的概率，简称为首达概率，称

$f_{ij}=\sum_{n=1}^{\infty} f_{ij}^{(n)}=P\Big(\bigcup_{n=1}^{\infty}(X_n=j,X_k\neq j,k=1,2,\cdots,n-1)|X_0=i\Big)$

为 $\{X_n,n\geq0\}$ 在 $0$ 时从状态 $i$ 出发，经过有限步转移后，迟早要达到状态 $j$ 的概率，简称为迟早概率，称

$f_{ij}^{(+\infty)}=P(X_n\neq j,n=1,2,\cdots,n-1)|X_0=i\Big)$

为 $\{X_n,n\geq0\}$ 在 $0$ 时从状态 $i$ 出发，永远也无法达到状态 $j$ 的概率

对于首达概率和迟早概率，其与马尔可夫链的转移概率有如下关系：

$\begin{align*} 0\leq& f_{ij}^{(n)} \leq p_{ij}^{(n)} \leq f_{ij} \leq 1 \\ p_{ij}^{(n)}&=\sum_{l=1}^n f_{ij}^{(l)}p_{jj}^{(n-l)} \\ f_{ij}^{(n)}&=\sum_{i_1\neq j}\sum_{i_2\neq j}\cdots\sum_{i_{n-1}\neq j} p_{ii_1}p_{i_1i_2}\cdots p_{i_{n-1}j} \end{align*}$

首达时刻

设马尔可夫链 $\{X_n,n\geq0\}$，当 $j\in S$，称

$T_j=\min \{n|n\geq 1,X_n=j\}$

为 $\{X_n,n\geq0\}$ 首次到达状态 $j$ 的时间，简称首达时刻，显然，$T_j$ 是一个随机变量

当 $\{n|n\geq 1,X_n=j\}=\varnothing$，即 $\forall n\geq 1,X_n\neq j$ 时，定义

$T_j=+\infty$

即系统在有限时间内，不可到达状态 $j$

首达时刻与首达概率和迟早概率有如下关系：

$\begin{align*} f_{ij}^{(n)}&=P(T_j=n|X_0=i)\\ f_{ij}&=P(T_j< +\infty|X_0=0) \end{align*}$

平均转移步数与平均返回时间

设马尔可夫链 $\{X_n,n\geq0\}$，当 $j\in S$ 时，其首达时刻为 $T_j$，称

$\mu_{ij}=E(T_j|X_0=i)=\sum_{n=1}^{\infty}n f_{ij}^{(n)}$

为从状态 $i$ 出发，首次到达状态 $j$ 的平均转移步数，称

$\mu_{jj}=E(T_j|X_0=j)=\sum_{n=1}^{\infty}n f_{jj}^{(n)}$

为从状态 $j$ 出发，首次返回状态 $j$ 的平均返回时间

周期

设马尔可夫链 $\{X_n,n\geq0\}$，当 $i\in S$，若 $\{n|n\geq 1,p_{ii}^{(n)}>0\}\neq \varnothing$，则称

$d_i=\text{GCD}\{n|n\geq 1,p_{ii}^{(n)}>0\}$

为状态 $i$ 的周期，若 $\{n|n\geq 1,f_{ii}^{(n)}>0\}\neq \varnothing$，则有

$h_i=\text{GCD}\{n|n\geq 1,f_{ii}^{(n)}>0\}$

对于 $d_i$ 和 $h_i$，有如下性质：

1）若 $p_{ij}^{(n)}>0$，则存在 $m\geq 1$，使得

$n=md_i$

2）若 $f_{ij}^{(n)}> 0$，则存在 $m’\geq 1$，使得

$n=m'h_i$

3）若 $d_i$ 和 $h_i$ 中一个存在，则另一个也存在，且

$d_i=h_i$

【状态】

可约与不可约

设马尔可夫链 $\{X_n,n\geq0\}$，对任意 $i,j\in S$，若存在任一时刻 $t>0$，满足：

$P(X_t=i|X_0=j)>0$

即在 $0$ 时刻从状态 $j$ 出发，在 $t$ 时刻到达状态 $i$ 的概率大于 $0$，则称马尔可夫链 $\{X_n,n\geq0\}$ 是不可约的，否则称是可约的

直观上，一个不可约的马尔可夫链，从任意状态出发，当经过充分长时间后，可以到达任意状态

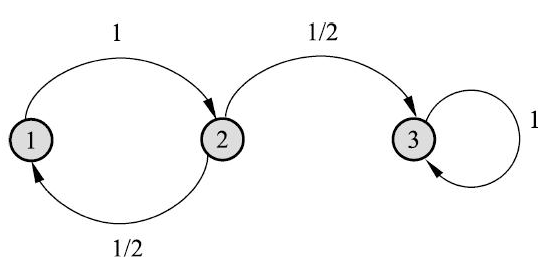
如下马尔可夫链状态转移图所示，其转移概率矩阵

$\begin{bmatrix} 0 & \frac{1}{2} & 0 \\ 1 & 0 & 0 \\ 0 & \frac{1}{2} & 1 \end{bmatrix}$

其平稳分布 $\pi=(0,0,1)^T$，即该马尔可夫链转移到状态 $3$ 后，就在该状态上循环，无法到达状态 $1$ 与状态 $2$，故该马尔可夫链是可约的

周期与非周期

设马尔可夫链 $\{X_n,n\geq0\}$，对任意 $i\in S$

若状态 $i$ 的周期 $d_i>1$，则称状态 $i$ 为周期为 $d_i$ 的周期状态，称该马尔可夫链为周期的
若状态 $i$ 的周期 $d_i=1$，则称状态 $i$ 为非周期状态，称该马尔可夫为非周期的

直观上，一个非周期性的马尔可夫链，不存在一个状态，从这个状态出发，再返回到这个状态时所经历的时间呈周期性

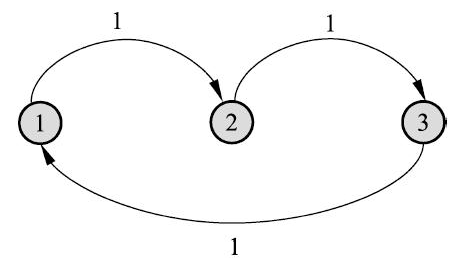
如下马尔可夫链状态转移图所示，其转移概率矩阵

$\begin{bmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix}$

其平稳分布 $\pi=(\frac{1}{3},\frac{1}{3},\frac{1}{3})^T$，即该马尔可夫链从每个状态出发，返回该状态的时刻都是 $3$ 的倍数，具备周期性，最终停留在每个状态的概率都是 $\frac{1}{3}$，故该马尔可夫链是周期的

常返与非常返

设马尔可夫链 $\{X_n,n\geq0\}$，对任意 $i\in S$

若从状态 $i$ 到状态 $i$ 的首达概率 $f_{ii}=1$，则称状态 $i$ 为常返状态或返回状态，称该马尔可夫链为常返的
若从状态 $i$ 到状态 $i$ 的首达概率 $f_{ii}<1$，则称状态 $i$ 为非常返状态或滑过状态，称该马尔可夫链为非常返的

正常返与零常返

设马尔可夫链 $\{X_n,n\geq0\}$，对任意 $i\in S$

若状态 $i$ 为常返状态，且状态 $i$ 的平均返回时间 $\mu_{ii}<+\infty$，则称状态 $i$ 为正常返状态，称该马尔可夫链为正常返的
若状态 $i$ 为常返状态，且状态 $i$ 的平均返回时间 $\mu_{ii}=+\infty$，则称状态 $i$ 为零常返状态或消极常返状态，称该马尔可夫链为零常返的

直观上，一个正常返的马尔可夫链，其中任意一个状态，从其他任意一个状态出发，当时间趋于无穷时，首次转移到这个状态的概率不为 $0$

对于不可约、非周期且正常返的马尔可夫链，有唯一平稳分布存在

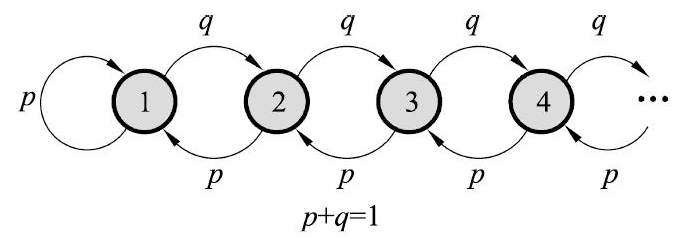
如下马尔可夫链状态转移图所示，其转移概率矩阵

$\begin{bmatrix} p & p & 0 & 0 & \cdots \\ q & 0 & p & 0 & \ddots \\ 0 & q & 0 & p & \ddots \\ 0 & 0 & q & 0 & \ddots \\ \vdots & \ddots & \ddots & \ddots & \ddots \end{bmatrix}$

当 $p>q$ 时，其平稳分布 $\pi=(\frac{q}{p})^i (\frac{p-q}{p}),i=1,2,\cdots$，即当时间趋于无穷时，转移到任何一个状态的概率不为 $0$，故该马尔可夫链是正常返的

当 $p\leq q$ 时，不存在平稳分布，故该马尔可夫链是零常返的

遍历与非遍历

设马尔可夫链 $\{X_n,n\geq0\}$，对任意 $i\in S$

若状态 $i$ 为不可约、正常返，且是非周期的，则称状态 $i$ 为正常返非周期状态或遍历状态，称该马尔可夫链为遍历的
若状态 $i$ 为不可约、正常返，且是周期的，则称状态 $i$ 为正常返周期状态或非遍历状态，称该马尔可夫链为非遍历的

不可约、正常返、非周期保证了当时间趋于无穷时，到达任一状态的概率不为 $0$

【遍历定理】

对于马尔可夫链的遍历状态，有如下的遍历定理

设马尔可夫链 $\{X_n,n\geq0\}$，若其是不可约、非周期、正常返的，即该马尔可夫链是遍历的，那么该马尔可夫链有唯一分布 $\pi=(\pi_1,\pi_1,\cdots)^T$，且转移概率的极限分布是马尔可夫链的平稳分布，即：

$\lim_{t\rightarrow \infty} P(X_t=i|X_0=j)=\pi_i,\quad i=1,2,\cdots;j=1,2,\cdots$

若 $f(X)$ 是定义在状态空间 $S$ 上的函数，且 $f(X)$ 关于平稳分布 $\pi=(\pi_1,\pi_1,\cdots)^T$ 的数学期望 $E_{\pi}[|f(X)|]=\sum\limits_i f(i) \pi_i<\infty$，则该函数的样本均值 $\hat{f_t}=\frac{1}{t}\sum\limits_{s=1}^t f(x_s)$ 以概率 $1$ 收敛于 $E_{\pi}[|f(X)|]$，即：

$P\{\hat{f_t}\rightarrow E_{\pi}[|f(X)|]\}=1$

遍历定理的直观解释是：满足不可约、非周期、正常返的马尔可夫链，当时间趋于无穷时，马尔可夫链的状态分布趋于平稳分布，随机变量的函数的样本均值以概率 $1$ 收敛于该函数的数学期望

遍历定理实际上表达了马尔可夫链遍历性的含义：样本均值可以认为是时间均值，数学期望可以认为是空间均值，当时间趋于无穷时，时间均值等同于空间均值

实际应用时，通常是取一个足够大的整数 $m$，经过 $m$ 次迭代后便认为状态分布就是平稳分布，此时从第 $m+1$ 次迭代到第 $n$ 次迭代的均值，被称为遍历均值，即：

$\hat{E}f=\frac{1}{n-m} \sum_{i=m+1}^{n} f(x_i)$

【状态的可达与互通】

设马尔可夫链 $\{X_n,n\geq0\}$，当 $i,j\in S$，若存在 $n\geq 1$，使得

$p_{ij}^{(n)}>0$

则称状态 $i$ 可达状态 $j$，记为 $i\rightarrow j$

若状态 $i$ 可达状态 $j$，且状态 $j$ 可达状态 $i$，即

$i\rightarrow j,j\rightarrow i$

则称状态 $i$ 与状态 $j$ 互通，记为 $i\leftrightarrow j$

对于状态的可达与互通，有：

可达的传递性：若 $i\rightarrow j,j\rightarrow k$，则 $i\rightarrow k$
互通的传递性：若 $i\leftrightarrow j,j\leftrightarrow k$，则 $i\leftrightarrow k$
互通的对称性：若 $i\leftrightarrow j$，则 $j\leftrightarrow i$

此外，对于互通的两个状态 $i,j\in S$，他们有相同的类型，即设 $i,j\in S$，且 $i\leftrightarrow j$，则 $i,j$ 有：

两者同为非常返状态
两者同为零常返状态
两者同为遍历状态
两者同为非遍历状态且周期相同