【引入】

随机过程的有限维分布函数族虽然是对随机过程的概率特征的完整描述，但在实际应用中却难以求得

同时，对于某些随机过程，为表征其概率特征，不一定要求出它的有限维分布函数族，只需要求出随机过程的几个表征值即可

为此，像概率论中研究随机变量的数字特征一样，给出随机过程的数字特征，其是利用随机变量的数字特征来定义的

【均值函数】

设 $\{X(t),t\in T\}$ 为一随机过程，$X(t)$ 为随机变量，若 $E[X(t)]$ 存在，记为 $\mu_X(t)$，称其为随机过程 $\{X(t),t\in T\}$ 的均值函数

若 $\{X(t),t\in T\}$ 的一维分布函数为 $F(t;x)$，那么

$\mu_X(t)=E[X(t)]=\int_{-\infty}^{+\infty} x dF(x),\quad t\in T$

随机过程的均值函数 $\mu_X(t)$ 在 $t$ 时刻的值表示随机过程在 $t$ 时刻所处状态取值的理论平均值，当 $t\in T$ 时，$\mu_X(t)$ 在几何上表示一条固定的曲线

设 $\{X(t),t\in T\}$ 为一随机过程，$X(t)$ 为随机变量，若 $D[X(t)]$ 存在，记为 $\sigma_X(t)$，称其为随机过程 $\{X(t),t\in T\}$ 的方差函数，有

$\sigma_X(t)=D[X(t)]=E[X(t)-\mu_X(t)]^2,\quad t\in T$

随机过程的方差函数 $\sigma_X(t)$ 在 $t$ 时刻的值表示随机过程在 $t$ 时刻所处状态取值偏离均值的偏差程度

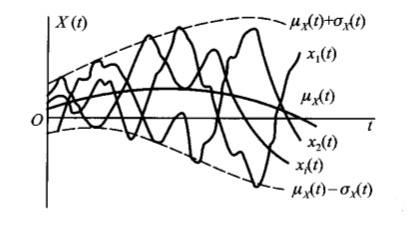
将随机过程的若干样本函数、均值函数、方差函数画到同一坐标系中，可以看到，均值函数刻画了随机过程在各时刻的摆动中心，方差函数刻画了随机过程在各时刻对均值的偏离程度

设 $\{X(t),t\in T\}$ 为一随机过程，对于 $\forall s,t \in T$，$X(t),X(s)$ 为两个随机变量，若 $Cov(X(s),X(t))$ 存在，记为 $C_X(s,t)$，称其为随机过程 $\{X(t),t\in T\}$ 的协方差函数，有

$\begin{align*} C_X(s,t) &=Cov(X(s),X(t)) \\ &=E\big[(X(s)-\mu_X(s))(X(t)-\mu_X(t))\big] \\ &=E[X(s)X(t)]-\mu_X(s)\mu_X(t)\\ \end{align*}$

随机过程的协方差函数 $C_X(s,t)$ 在 $s,t\in T$ 时刻的值表示随机过程在 $s,t$ 时刻所处状态的线性联系的密切程度

若 $C_X(s,t)$ 的绝对值较大，说明在两个时刻 $s,t$ 的状态 $X(s)$ 和 $X(t)$ 的线性联系较为密切；若 $C_X(s,t)$ 的绝对值较小，说明在两个时刻 $s,t$ 的状态 $X(s)$ 和 $X(t)$ 的线性联系不密切

设 $\{X(t),t\in T\}$ 为一随机过程，对于 $\forall s,t \in T$，$X(t),X(s)$ 为两个随机变量，若 $E[X(s)X(t)]$ 存在，记为 $R_X(s,t)$，称其为随机过程 $\{X(t),t\in T\}$ 的相关函数，有

$R_X(s,t)=E[X(s)X(t)]$

随机过程的相关函数 $R_X(s,t)$ 在 $s,t\in T$ 时刻的值表示随机过程在 $s,t$ 时刻所处状态的线性相关关系

设 $\{X(t),t\in T\}$ 为一随机过程，$X(t)$ 为随机变量，若 $E[X(t)]^2$ 存在，记为 $\Phi_X(t)$，称其为随机过程 $\{X(t),t\in T\}$ 的均方值函数

若 $\{X(t),t\in T\}$ 的一维分布函数为 $F(t;x)$，那么

$\Phi_X(t)=E[X(t)]^2=\int_{-\infty}^{+\infty} x^2 dF(x),\quad t\in T$

随机过程 $\{X(t),t\in T\}$ 的协方差函数、相关函数、均值函数的关系为

$C_X(s,t)=R_X(s,t)-\mu_X(s)\mu_X(t),\quad s,t\in T$

在协方差函数的定义式中，取 $s=t$，则随机过程的方差函数和协方差函数的关系为

$D_X(t)=C_X(t,t),\quad t\in T$

类似地，均方值函数和相关函数的关系为

$\Phi_X(t)=R_X(t,t),\quad t\in T$

从上述关系可看出，均值函数和相关函数是随机过程的两个本质数字特征，其他的数字特征可以通过这个两个本质数字特征获得

此外，随机过程的均值函数也被称为随机过程的一阶矩，均方值函数也被随机过程的二阶矩