常见概率分布

Reference

• 概率论学习笔记（二）
• 几种常见的数学分布
• 常用分布
• 几个常见的离散型概率分布
• 帕斯卡分布
• 负二项分布
• 机器学习：Multinoulli分布与多项式分布

【离散分布】

伯努利试验

满足以下描述的试验，被称为伯努利试验（Bernoulli experiment）

1. 试验只能有互斥的两种结果，发生或不发生，成功或失败
2. 每次试验中，某种结果发生的概率是 $p$，另一种结果发生的概率是 $1-p$
3. 试验是互相独立的，且可重复进行 $n$ 次

伯努利试验，对应的现实场景是有放回抽样

伯努利分布

伯努利分布（Bernoulli Distribution）又称 0-1 分布、两点分布，用于描述一次伯努利试验中是否成功

记 $X$ 为一次伯努利试验中事件 $A$ 成功的次数，则 $X=0,1$，假设事件 $A$ 发生的概率为 $p$，那么称 $X$ 服从参数为 $1,p$ 的伯努利分布，记作 $X\sim B(1,p)$

$X$ 的概率分布为：

$$P(X=x)=p^x(1-p)^{1-x},\quad x=0,1$$

即：

$$P(X=1)=p \quad P(X=0)=1-p$$

---

伯努利分布的数学期望和方差分别为：

• $EX=p$
• $DX=p(1-p)$

伯努利分布的特征函数为：

$$\varphi(t)=pe^{jt}+q$$

二项分布

二项分布（Binomial Distribution）又称 $n$ 重伯努利分布，用于描述 $n$ 次伯努利试验中成功的次数

记 $X$ 为 $n$ 重伯努利试验中事件 $A$ 成功的次数，则 $X=0,1,2,\cdots,n$，假设事件 $A$ 发生的概率为 $p$，那么称 $X$ 服从参数为 $n,p$ 的伯努利分布，记作 $X\sim B(n,p)$

$X$ 的概率分布为：

$$P(X=k)= \left(\begin{array}{c}n\\k\end{array}\right) p^k(1-p)^{n-k},\quad k=0,1,\cdots,n$$

在独立条件下，二项分布对于其中的参数 $n$ 具有可加性，即：$X_1\sim B(n_1,p)$，$X_2\sim B(n_2,p)$，且 $X_1,X_2$ 独立，有 $X_1+X_2\sim B(n_1+n_2,p)$

进一步，服从 $B(n,p)$ 的随机变量可以看作是 $n$ 个相互独立的服从伯努利分布 $B(1,p)$ 的随机变量之和

---

二项分布的数学期望和方差分别为：

• $EX=np$
• $DX=np(1-p)$

二项分布的特征函数为：

$$\varphi(t)=(pe^{jt}+q)^n$$

几何分布

几何分布（Geometric Distribution）用于描述伯努利试验序列中，事件 $A$ 首次出现的试验次数

重复进行伯努利试验，直到事件 $A$ 发生为止才停下，记 $X$ 为若干次伯努利试验中事件 $A$ 进行的次数，则 $X=1,2,\cdots$，假设事件 $A$ 发生的概率为 $p$，那么称 $X$ 服从参数为 $p$ 的几何分布，记作 $X\sim G(p)$

$X$ 的概率分布为：

$$P(X=k)=(1-p)^{k-1}p,\quad k=1,2,...$$

几何分布具有无记忆性：若 $X\sim G(p)$，对 $\forall n,m\in Z^+$，有

$$P(X>n+m|X>m)=P(X>n)$$

该性质表明，在前 $m$ 次试验中 $A$ 没有出现的条件下，则在接下去的 $n$ 次试验中 $A$ 仍未出现的概率只与 $n$ 有关，而与以前的 $m$ 次试验无关，似乎忘记了前 $m$ 次试验结果

---

几何分布的数学期望和方差分别为：

• $EX=\frac{1}{p}$
• $DX=\frac{1-p}{p^2}$

几何分布的特征函数为：

$$\varphi(t)=\frac{pe^{jt}}{1-qe^{jt}}$$

负二项分布与帕斯卡分布

负二项分布（Negative Binomial Distribution）用于描述伯努利试验序列中，事件 $A$ 第 $r$ 次出现时的试验次数

重复进行伯努利试验，直到事件 $A$ 发生第 $r$ 次时才停下，记 $X$ 为若干次伯努利试验中事件 $A$ 进行的次数，则 $X=r,r+1,\cdots$，假设事件 $A$ 发生的概率为 $p$，那么称 $X$ 服从参数为 $r,p$ 的负二项分布，记作 $X\sim NB(r,p)$

$X$ 的概率分布为：

$$P(X=k)=\left(\begin{array}{c}k-1\\r-1\end{array}\right) (1-p)^{k-1}p,\quad k=r,r+1,...$$

当 $r$ 为整数时，称 $X$ 服从参数为 $r,p$ 的帕斯卡分布（Pascal Distribution），记作 $X\sim Pas(r,p)$

需要注意的是，尽管很难想象一个非整数的失败次数，但这个分布是通过概率密度函数在形式上严格定义的

可以发现，当 $r=1$ 时，帕斯卡分布即几何分布，即：$Pas(1,p)=G(p)$

与二项分布类似，帕斯卡分布对于其中的参数 $r$ 具有可加性，即：$X_1\sim Pas(r_1,p)$，$X_2\sim Pas(r_2,p)$，且 $X_1,X_2$ 独立，有 $X_1+X_2\sim Pas(r_1+r_2,p)$

进一步，服从帕斯卡分布 $Pas(r,p)$ 的随机变量可以看作是 $r$ 个相互独立的服从几何分布 $G(p)$ 的随机变量之和

---

负二项分布的数学期望和方差分别为：

• $EX=\frac{r}{p}$
• $DX=\frac{r(1-p)}{p^2}$

负二项分布的特征函数为：

$$\varphi(t)=(\frac{pe^{jt}}{1-qe^{jt}})^t$$

泊松分布

泊松分布（Poisson Distribution）常与单位时间、单位面积、单位体积上的计数过程相联系

记 $X$ 为某个随机事件 $A$ 发生的次数，则 $X=0,1,2,\cdots,n$，假设每次事件 $A$ 是否发生相互独立，且事件 $A$ 平均发生 $\lambda$ 次，那么 $X$ 服从参数为 $\lambda$ 的泊松分布，记为 $X\sim P(\lambda)$

$X$ 的概率分布为：

$$P(X=k)=\frac{\lambda^k}{k!}e^{-\lambda},\quad k=0,1,2,\cdots$$

与二项分布类似，泊松分布在独立条件下对于参数 $\lambda$ 具有可加性，即：$X_1\sim P(\lambda_1)$，$X_2\sim P(\lambda_2)$，且 $X_1,X_2$ 独立，有 $X_1+X_2\sim P(\lambda_1+\lambda_2)$

事实上，泊松分布本质上是 $n\rightarrow \infty$ 时的二项分布，即若 $\lim\limits_{n\rightarrow \infty} np_n=\lambda,0<p_n<1$，则有：

$$\lim\limits_{n\rightarrow \infty} \left(\begin{array}{c}n\\k\end{array}\right) p_n^k(1-p_n)^{n-k} = \frac{\lambda^k}{k!}e^{-\lambda}$$

也就是说，当 $n$ 足够大，且此时平均发生的事件数趋于常数 $\lambda$ 时，二项分布 $B(n,p_n)$ 实质上就是泊松分布 $P(\lambda)$

---

泊松分布的数学期望和方差分别为：

• $EX=\lambda$
• $DX=\lambda$

泊松分布的特征函数为：

$$\varphi(t)=e^{\lambda(e^{jt}-1)}$$

超几何分布

超几何分布（Hypergeometric Distribution）用于描述 $N$ 个产品中不放回的随机抽取 $n$ 个的次品数

设有 $N$ 个产品，其中有 $M(M\leq N)$ 个次品，从中不放回的随机抽取 $n(n\leq N)$ 个，记 $X$ 为这 $n$ 个中的次品数，则 $X=0,1,\cdots,\min\{M,n\}$，称 $X$ 服从参数为 $n,N,M$ 的超几何分布，记作 $X\sim H(n,M,N)$

$X$ 的概率分布为：

$$P(X=k) = \frac{ \left(\begin{array}{c}M\\k\end{array}\right) \left(\begin{array}{c}N-M\\n-k\end{array}\right) }{ \left(\begin{array}{c}N\\n\end{array}\right) },\quad k=0,1,\cdots,\min\{M,n\}$$

当次品数 $M$ 只与产品数 $N$ 相关时，且 $\lim\limits_{N\rightarrow\infty}\frac{M}{N}=p\in(0,1)$，则有：

$$\lim_{N\rightarrow\infty} \frac{ \left(\begin{array}{c}M\\k\end{array}\right) \left(\begin{array}{c}N-M\\n-k\end{array}\right) }{ \left(\begin{array}{c}N\\n\end{array}\right) } = \left(\begin{array}{c}M\\k\end{array}\right) p^k(1-p)^{n-k}$$

也就是说，当总量 $N$ 足够大时，若次品率 $\frac{M}{N}$ 趋于一个常数 $p$，那么进行无放回抽取（超几何分布）可以近似为有放回抽取（二项分布）

---

超几何分布的数学期望和方差分别为：

• $EX=\frac{nM}{N}$
• $DX=\frac{nM(N-m)(N-n)}{N^2(N-1)}$

超几何分布的特征函数为：

$$f(t) = \sum_{k=0}^{\infty} \frac{t^k}{k!} \binom{n}{k} p^k (1-p)^{n-k}$$

【连续分布】

正态分布

若随机变量 $X$ 的概率密度函数为：

$$f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}},\quad -\infty<x+\infty$$

则称 $X$ 服从参数为 $\mu,\sigma^2$ 的正态分布，记作 $X\sim N(\mu,\sigma^2)$，其中 $\mu$ 为位置参数，用于控制曲线在 $x$ 上的位置，$\sigma$ 为尺度参数，用于控制曲线的形状

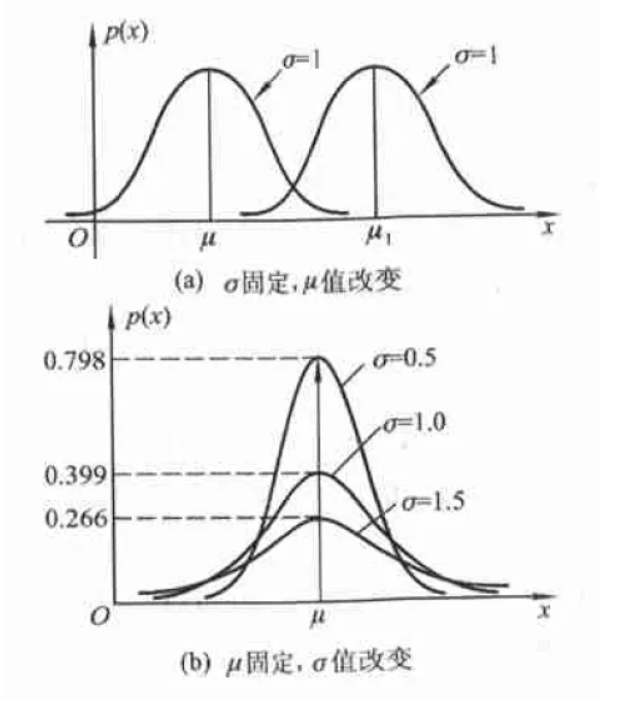
容易看出，其具备如下性质：

• $f(x)$ 关于 $x=\mu$ 对称
• $f(\mu)$ 为最大值
• $x=\mu\pm\sigma$ 为拐点

其分布函数为：

$$F(x)=\int_{-\infty}^x\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(t-\mu)^2}{2\sigma^2}}dt$$

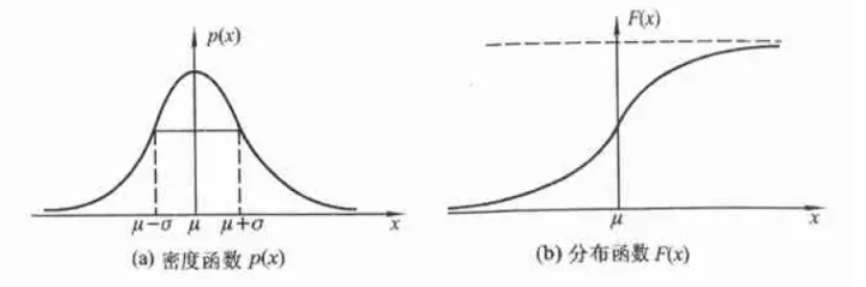
当 $\mu=0,\sigma^2=1$ 时，有 $X\sim N(0,1)$，此时称正态分布为标准正态分布，此时概率密度函数和分布函数分别为：

$$\begin{align*} \varphi(x) &= \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} \\ \Phi(x) &= \int_{-\infty}^x \frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}} dt \end{align*}$$

故有：若 $X~\sim N(\mu,\sigma^2)$，则

• $P(X\leq a) = \Phi(\frac{a-\mu}{\sigma})$
• $P(a\leq X \leq b)=\Phi(\frac{b-\mu}{\sigma})-\Phi(\frac{a-\mu}{\sigma})$

任何一个正态变量均可通过标准化转换为标准正态分布，即若 $X\sim N(\mu,\sigma^2)$，有：

$$X^* = \frac{X-\mu}{\sigma}\sim N(0,1)$$

故有：若 $X\sim N(0,1)$，则

• $\Phi(-a)=1-\Phi(a)$
• $P(X>a)=1-\Phi(a)$
• $P(a<X<b)=\Phi(b)-\Phi(a)$
• $P(|X|<c)=2\Phi(c)-1$

---

正态分布的数学期望和方差分别为：

• $EX=\mu$
• $DX=\sigma^2$

正态分布的特征函数为：

$$\varphi(t) = e^{jt\mu - \frac{1}{2}\sigma^2t^2}$$

均匀分布

若随机变量 $X$ 的概率密度函数为：

$$f(x)= \left\{\begin{align*} \frac{1}{b-a}, && a<x<b \\ 0,&& 其他 \end{align*}\right.$$

则称 $X$ 服从区间 $(a,b)$ 上的均匀分布，记作 $X\sim U(a,b)$

其分布函数为：

$$F(x)= \left\{\begin{align*} 0,&& x<a \\ \frac{x-a}{b-a}, && a\leq x<b \\ 1,&& x\geq b \end{align*}\right.$$

---

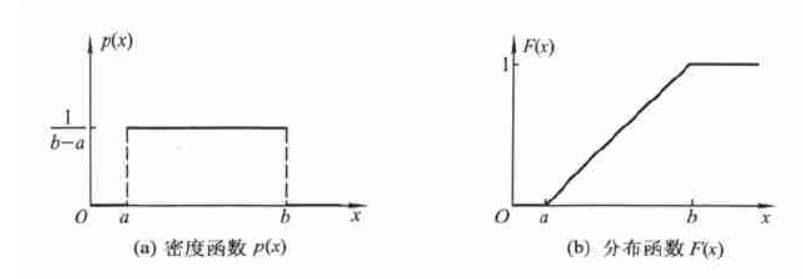
均匀分布的数学期望和方差分别为：

• $EX=\frac{a+b}{2}$
• $DX=\frac{(b-a)^2}{12}$

均匀分布的特征函数为：

$$\varphi(t)=\frac{e^{jtb}-e^{jta}}{jt(b-a)}$$

指数分布

指数分布是一种偏态分布，随机变量只可能取非负实数，常被用作各种寿命分布，譬如电子元器件的寿命、动物的寿命、电话的通话时间、随机服务系统中的服务时间等，其在可靠性与排队论中有着广泛的应用

若随机变量 $X$ 的概率密度函数为：

$$f(x)= \left\{\begin{align*} \lambda e^{-\lambda x}, && x\geq 0 \\ 0,&& x<0 \end{align*}\right.$$

则称 $X$ 服从参数为 $\lambda$ 的指数分布，记作 $X\sim E(\lambda)$

其分布函数为：

$$F(x)= \left\{\begin{align*} 1-e^{\lambda x},&& x\geq a \\ 0, && x< 0 \end{align*}\right.$$

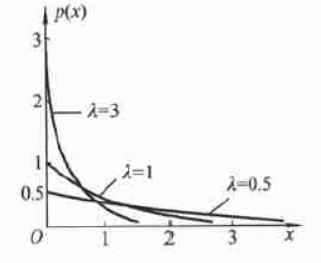
与几何分布类似，指数分布具有无记忆性：若 $X\sim E(\lambda)$，对 $\forall t,s>0$，有

$$P(X>t+s|X>s)=P(X>t)$$

---

指数分布的数学期望和方差分别为：

• $EX=\frac{1}{\lambda}$
• $DX=\frac{1}{\lambda^2}$

指数分布的特征函数为：

$$\varphi(t) = \frac{\lambda}{\lambda-jt}$$

伽马分布

首先引入伽马函数：

$$\Gamma(\alpha)=\int_{0}^{+\infty} x^{\alpha-1}e^{-x}dx,\quad a>0$$

其具有如下性质：

• $\Gamma(1)=1,\Gamma(\frac{1}{2})=\sqrt{\pi}$
• $\Gamma(\alpha+1)=\alpha\Gamma(\alpha)$
• $\Gamma(n+1)=n\Gamma(n)=n!$，其中 $n$ 为自然数

若随机变量 $X$ 的概率密度函数为：

$$f(x)= \left\{\begin{align*} \frac{\lambda^\alpha}{\Gamma(\alpha)}x^{\alpha-1} e^{-\lambda x}, && x\geq 0 \\ 0,&& x<0 \end{align*}\right.$$

则称 $X$ 服从参数为 $\alpha,\lambda$ 的伽马分布，记作 $X\sim \Gamma(\alpha,\lambda)$，其中 $\alpha>0$ 为形状参数，$\lambda>0$ 为尺度参数

可以发现，当 $\alpha=1$ 时，伽马分布即指数分布，即 $\Gamma(1,\lambda)=E(\lambda)$

与二项分布类似，伽马分布对于其中的参数 $\alpha$ 具有可加性，即：$X_1\sim \Gamma(\alpha_1,\lambda)$，$X_2\sim \Gamma(\alpha_2,\lambda)$，且 $X_1,X_2$ 独立，有 $X_1+X_2\sim \Gamma(\alpha_1+\alpha_2,\lambda)$

进一步，服从伽马分布 $\Gamma(\alpha,\lambda)$ 的随机变量可以看作是 $\alpha$ 个相互独立的服从指数分布 $E(p)$ 的随机变量之和

此外，当 $\alpha=\frac{n}{2},\lambda=\frac{1}{2}$ 时，伽马分布 $\Gamma(\frac{n}{2},\frac{1}{2})$ 为自由度为 $n$ 的卡方分布，记作 $\chi^2(n)$

---

伽马分布的数学期望和方差分别为：

• $EX=\frac{\alpha}{\lambda}$
• $DX=\frac{\alpha}{\lambda^2}$

伽马分布的特征函数为：

$$\varphi(t) = \frac{1}{(1 - jt\lambda)^\alpha}$$

贝塔分布

首先引入贝塔函数：

$$B(a,b)=\int_{0}^{1} x^{\alpha-1}(1-x)^{b-1}dx,\quad a,b>0$$

其具有如下性质：

• $B(a,b)=B(b,a)$
• $B(a,b)=\frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}$

若随机变量 $X$ 的概率密度函数为：

$$f(x)= \left\{\begin{align*} \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}x^{a-1} (1-x)^{b-1}, && 0<x<1 \\ 0,&& 其他 \end{align*}\right.$$

则称 $X$ 服从参数为 $a,b$ 的贝塔分布，记作 $X\sim Be(a,b)$，其中 $a,b>0$ 均为形状参数

---

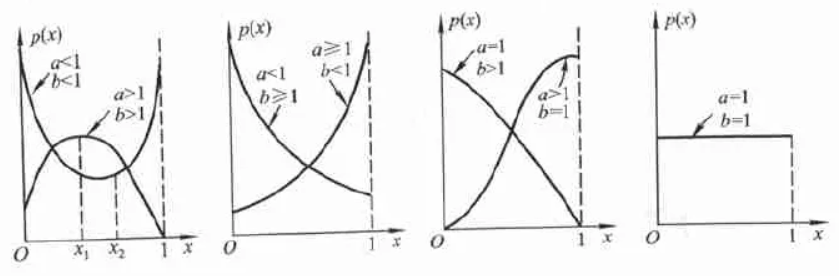
贝塔分布的数学期望和方差分别为：

• $EX=\frac{a}{a+b}$
• $DX=\frac{ab}{(a+b)^2(a+b+1)}$

【随机向量的分布】

多项分布

多项分布（Multinomial Distribution）是二项分布的推广

独立进行 $N$ 次伯努利试验，设 $A_1,A_2,\cdots,A_n$ 为完备事件组，用 $X_i$ 表示事件 $A_i$ 发生的次数，若事件 $A_i$ 发生的概率为 $p_i$，那么称 $\mathbf{X}=(X_1,X_2,\cdots,X_n)$ 服从多项分布，记作 $\mathbf{X} \sim PN(N,p_1,p_2,\cdots,p_r)$

$\mathbf{X}$ 的概率分布为：

$$P(X_1=k_1,\cdots,X_n=k_n) = \left(\begin{array}{ccc} &N& \\k_1 &\cdots &k_n\end{array}\right)p_1^{k_1}\cdots p_r^{k_n}$$

其中，$k_i\geq0$，且 $k_1+\cdots+k_n=N$

二维正态分布

若随机变量 $(X,Y)$ 的联合概率密度为：

$$f(x,y)=\frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}} e^{\Big[ -\frac{1}{2(1-\rho^2)} \big( \frac{(x-\mu_1)^2}{\sigma_1^2} - \frac{2\rho(x-\mu_1)(y-\mu_2)}{\sigma_1\sigma_2} + \frac{(y-\mu_2)^2}{\sigma_2^2} \big) \Big]}$$

其中，$\sigma_1,\sigma_2 >0,-1<\rho<1$

则称 $(X,Y)$ 服从参数为 $\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho$ 的二维正态分布，记作 $(X,Y)\sim N(\mu_1,\mu_2,\sigma_1^2,\sigma_2^2,\rho)$

$X,Y$ 的边缘密度均为正态分布，且参数分别来自二维正态分布中的 $\sigma_1,\sigma_2,\mu_1,\mu_2$ ，与 $\rho$ 无关，即：

$$\begin{align*} f_X(x) &= \frac{1}{\sqrt{2\pi\sigma_1^2}}e^{-\frac{(x-\mu_1)^2}{2\sigma_1^2}} \\ f_Y(y) &= \frac{1}{\sqrt{2\pi\sigma_2^2}}e^{-\frac{(y-\mu_2)^2}{2\sigma_2^2}} \end{align*}$$

故有： $X\sim N(\mu_1,\sigma_1^2),Y\sim N(\mu_2,\sigma_2^2)$

进一步可得，$X,Y$ 独立的充要条件为：$\rho=0$

二维均匀分布

二维均匀分布是均匀分布的推广

设 $D\in \mathbb{R}^2$，$m(D)$ 为其面积，若 $(X,Y)$ 有联合概率密度：

$$f(x,y)= \left\{\begin{align*} \frac{1}{m(D)}, && (x,y)\in D \\ 0,&& 其他 \end{align*}\right.$$

则称 $(X,Y)$ 服从 $D$ 上的均匀分布