梯度下降法的优化算法

【指数加权平均】

指数加权平均（Exponentially Weight Average）是一种常用的序列数据处理方式，通常用于序列分析，例如金融序列分析、温度变化序列分析等

其过程如下：

$$S_t=\left\{ \begin{array}{cc} Y_1, & t=1 \\ \beta S_{t-1}+(1-\beta) Y_t,& t>1 \end{array} \right.$$

其中，$Y_t$ 为 $t$ 下的实际值，$S_t$ 为 $t$ 下加权平均后的值，$\beta$ 为偏差修正值

假设给定一个序列，例如某地一百天每天的气温值，图中蓝色的点代表真实数据

这样的气温值的变化可以理解为优化的过程波动较大、异常较多，使用指数加权平均可以使波动变得平缓一些

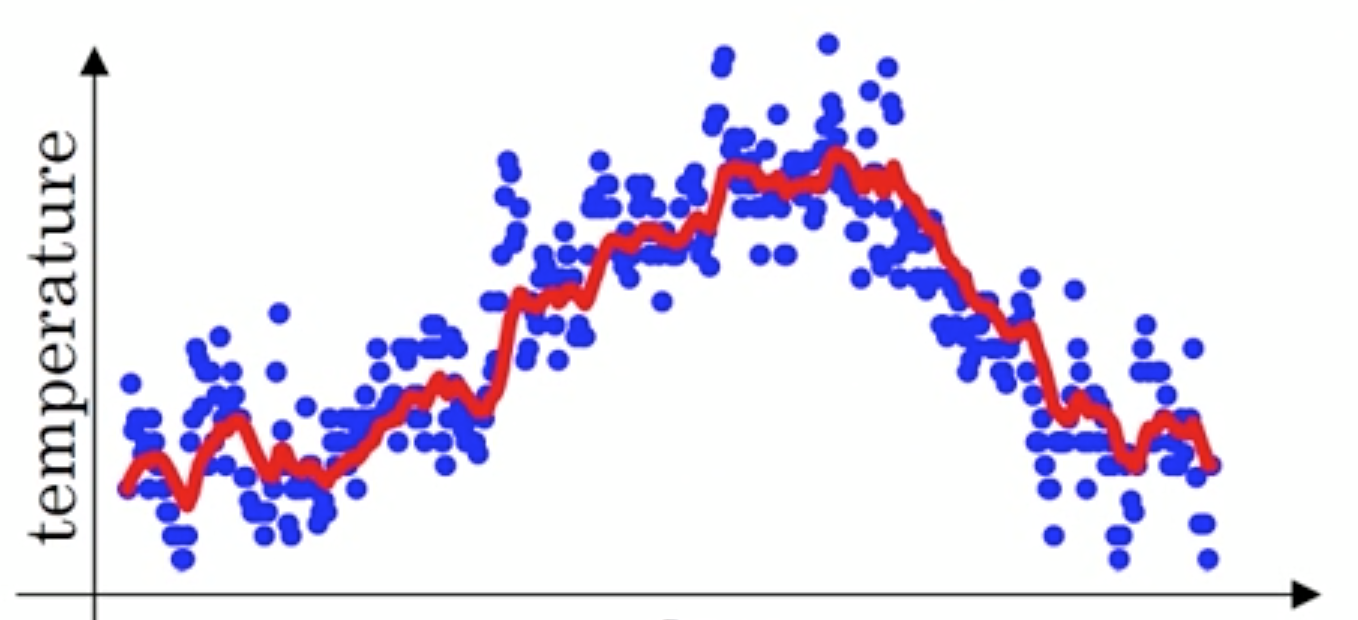
假设 $\beta=0.9$，那么对于这一百天的温度 $Y_i$，有：

$$\begin{gather*} S_1 = Y_1 \\ S_2 = 0.9S_1 + 0.1Y_2 \\ S_3 = 0.9S_2 + 0.1Y_3 \\ \vdots \\ S_{100} = 0.9S_{99} + 0.1Y_{100} \end{gather*}$$

那么对于第 $100$ 天的结果，合并后有：

$$S_{100} = 0.1 Y_{100} + 0.1 * 0.9 Y_{9} + 0.1 *(0.9)^2Y_{98}+\cdots+0.1*(0.9)^{99} Y_1$$

相当于第 $100$ 天的结果占较大比重，之前的 $99$ 天对结果的影响逐步降低

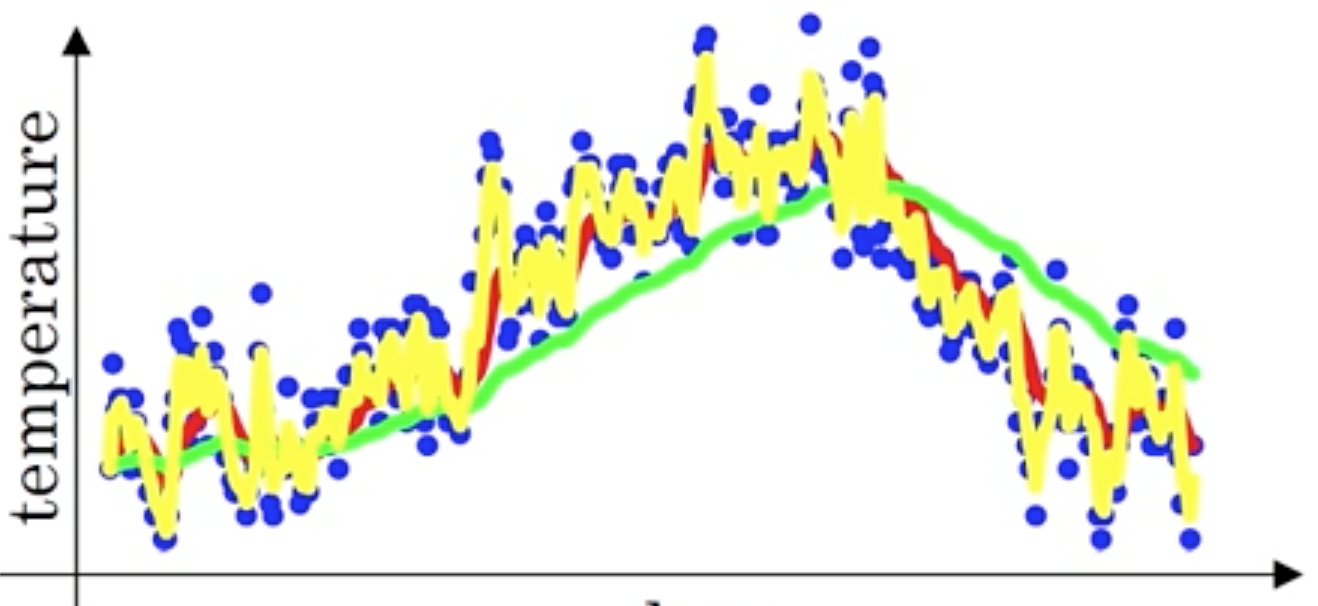
$\beta$ 被称为偏差修正（Bias Correction），其越大相当于求取平均利用的实际值越多，曲线就会越平滑且越滞后

如下图所示，当取 $\beta=0.98$ 时，得到图中更为平滑的绿色曲线，当取 $\beta=0.5$ 时，得到图中噪点更多的黄色曲线

上述点的数据，可以理解成梯度下降的过程，通过指数加权平均，可以在每一次迭代中优化计算出的梯度值

【动量梯度下降】

动量梯度下降（Gradient Descent with Momentum）是计算梯度的指数加权平均数，并利用该值来更新参数值

对于梯度下降法，其一般形式为：

$$\boldsymbol{\theta}_{k+1} = \boldsymbol{\theta}_{k} -\alpha \triangledown_k J(\boldsymbol{\theta})$$

可以看到，每次更新仅与当前梯度 $ \triangledown_k J(\boldsymbol{\theta})$ 相关，不涉及之前的梯度，那么对于 $n$ 次梯度下降中求得的梯度序列：

$$\{ \triangledown_1 J(\boldsymbol{\theta}), \triangledown_2 J(\boldsymbol{\theta}), \cdots, \triangledown_n J(\boldsymbol{\theta}) \}$$

其对应的动量梯度为：

$$\begin{gather*} S_0 = 0 \\ S_1 = \beta S_0 + (1-\beta) \triangledown_1 J(\boldsymbol{\theta}) \\ S_2 = \beta S_1 + (1-\beta) \triangledown_2 J(\boldsymbol{\theta}) \\ \vdots \\ S_n = \beta S_{n-1} + (1-\beta) \triangledown_n J(\boldsymbol{\theta}) \\ \end{gather*}$$

那么，动量梯度下降法的更新过程为：

$$\boldsymbol{\theta}_{k+1} = \boldsymbol{\theta}_{k} -\alpha S_k$$

当前后梯度方向一致时，动量梯度下降能够加速学习，而前后梯度方向不一致时，动量梯度下降能够抑制震荡

可以将动量梯度下降形象的理解为：将小球从一定高度扔下，其在下落时由于加速度的存在会越来越快，但由于 $\beta$ 的存在，使其不会一直加速运行，而是限定在一个范围内

如下图所示，蓝色的箭头代表使用随机梯度下降的过程，红色或者紫色的箭头代表使用动量梯度下降的过程，其通过累加过去的梯度值来减少抵达最小值路径上的摆动

【RMSProp 算法】

RMSProp（Root Mean Square Prop）算法是在对动量梯度下降法的基础上，引入平方和平方根

对于梯度下降法，其一般形式为：

$$\boldsymbol{\theta}_{k+1} = \boldsymbol{\theta}_{k} -\alpha \triangledown_k J(\boldsymbol{\theta})$$

对于 $n$ 次梯度下降中求得的梯度序列：

$$\{ \triangledown_1 J(\boldsymbol{\theta}), \triangledown_2 J(\boldsymbol{\theta}), \cdots, \triangledown_n J(\boldsymbol{\theta}) \}$$

其对应的动量梯度引入平方和后，有：

$$\begin{gather*} V_0 = 0 \\ V_1 = \beta V_0 + (1-\beta) (\triangledown_1 J(\boldsymbol{\theta}))^2 \\ V_2 = \beta V_1 + (1-\beta) (\triangledown_2 J(\boldsymbol{\theta}))^2 \\ \vdots \\ V_n = \beta V_{n-1} + (1-\beta) (\triangledown_n J(\boldsymbol{\theta}))^2 \\ \end{gather*}$$

进一步，在动量梯度下降法的更新过程的基础上引入平方根，此时梯度更新方程为：

$$\boldsymbol{\theta}_{k+1} = \boldsymbol{\theta}_{k} -\alpha \frac{\triangledown_k J(\boldsymbol{\theta})}{\sqrt{V+\varepsilon}}$$

其中，$\varepsilon$ 是一极小的数，防止分母太小导致不稳定

RMSProp 算法之所以引入平方和平方根，是考虑到 $\triangledown_k J(\boldsymbol{\theta})$ 较大时造成的下降摆动，在引入平方和后，当 $\triangledown_k J(\boldsymbol{\theta})$ 较大时，$(\triangledown_k J(\boldsymbol{\theta}))^2$ 更大，使得 $V_k$ 较小，进而使得 $\frac{\triangledown_k J(\boldsymbol{\theta})}{\sqrt{V_k+\varepsilon}}$ 变得非常小，使得每次梯度更新缓慢下降，进一步减少抵达最小值路径上的摆动，同时，其允许使用一个较大的学习率 $\alpha$ 来加快学习速度

【Adam 算法】

动量梯度下降法将下降梯度限定在一个较大的范围内，虽然能够减少抵达最小值路径上的摆动，但可能由于限制过小使得最终结果在收敛值附近摆动

而 RMSProp 算法在动量梯度下降法的基础上引入平方和，使得每次梯度更新缓慢下降，进一步减少抵达最小值路径上的摆动，但这可能造成更新梯度过小，使得收敛速度变慢

自适应矩估计（Adaptive Moment Estimation，Adam）算法是动量梯度下降法和 RMSProp 算法的结合，其不仅有效解决了抵达最小路径上的摆动，而且还提高了更新梯度，有效提高了收敛速度

对于梯度下降法，其一般形式为：

$$\boldsymbol{\theta}_{k+1} = \boldsymbol{\theta}_{k} -\alpha \triangledown_k J(\boldsymbol{\theta})$$

对于 $n$ 次梯度下降中求得的梯度序列：

$$\{ \triangledown_1 J(\boldsymbol{\theta}), \triangledown_2 J(\boldsymbol{\theta}), \cdots, \triangledown_n J(\boldsymbol{\theta}) \}$$

先计算对应的动量梯度：

$$\begin{gather*} S_0 = 0 \\ S_1 = \beta_1 S_0 + (1-\beta_1) \triangledown_1 J(\boldsymbol{\theta}) \\ S_2 = \beta_1 S_1 + (1-\beta_1) \triangledown_2 J(\boldsymbol{\theta}) \\ \vdots \\ S_n = \beta_1 S_{n-1} + (1-\beta_1) \triangledown_n J(\boldsymbol{\theta}) \\ \end{gather*}$$

然后计算引入平方和后的动量梯度：

$$\begin{gather*} V_0 = 0 \\ V_1 = \beta_2 V_0 + (1-\beta_2) (\triangledown_1 J(\boldsymbol{\theta}))^2 \\ V_2 = \beta_2 V_1 + (1-\beta_2) (\triangledown_2 J(\boldsymbol{\theta}))^2 \\ \vdots \\ V_n = \beta_2 V_{n-1} + (1-\beta_2) (\triangledown_n J(\boldsymbol{\theta}))^2 \\ \end{gather*}$$

进一步，在两种动量梯度的基础上，求偏差较正项( Bias-correction Term)，其通过滑动平均值的思想来增大动量梯度，从而完成对动量梯度的修正，即有：

$$\begin{gather*} S^{\text{corrected}}_k = \frac{S_k}{1-(\beta_1)^k} \\ V^{\text{corrected}}_k = \frac{V_k}{1-(\beta_2)^k} \\ \end{gather*}$$

于是，最终的梯度更新方程为：

$$\boldsymbol{\theta}_{k+1} = \boldsymbol{\theta}_{k} -\alpha \frac{S_k^{\text{corrected}}}{\sqrt{V_k^{\text{corrected}}}+\varepsilon}$$

需要注意的是，除了 $\alpha$ 为超参外，Adam 算法中涉及到两个偏差修正值 $\beta_1$ 和 $\beta_2$，以及一个保证分母不会太小而导致不稳定极小数 $\varepsilon$，对于这三个超参，Adam 算法的作者建议取 $\beta_1=0.9,\beta_2=0.999,\varepsilon=10^{-8}$