深度学习的过拟合与欠拟合问题

References：

• 【深度学习理论】一文搞透Dropout、L1L2正则化/权重衰减
• 深度学习之11——正则化
• Improving neural networks by preventing co-adaptation of feature detectors
• 神经网络中的随机失活方法
• 深度学习技巧之Early Stopping（早停法）
• Data Augmentation—数据增强解决你有限的数据集
• 数据增强(Data Augmentation)

【概述】

在 机器学习的模型评估 中，介绍了偏差、方差、噪声、偏差-方差分解以及偏差-方差窘境

当模型训练不足的情况下，偏差主导泛化误差，此时高偏差会导致欠拟合现象的发生；在模型训练充足的情况下，方差主导泛化误差，此时高方差会导致过拟合现象的发生

在 机器学习的模型选择 中，介绍了机器学习中解决欠拟合和过拟合现象的方法，对于深度学习来说，解决方法如下表：

过拟合	欠拟合
正则化（Regularization）	添加隐藏层
随机失活（Dropout）	添加神经元数量
早停止（Early Stopping）	更换损失函数
数据增强	增加训练轮次
寻找更适合的网络结构	寻找更合适的网络结构

【正则化】

对于一个隐藏层包含足够多的神经元的多层前馈神经网络，能够以任意精度逼近任意复杂度的连续函数，但如何设置隐藏层神经元个数仍然是个未解问题，正因为多层前馈神经网络强大的表示能力，BP 神经网络经常会出现过拟合现象

正则化（Regularizatoin）是机器学习的回归问题中最常用的模型选择方法之一，用于选择经验风险与模型复杂度同时较小的模型，其是结构风险最小化策略的实现，即在经验风险的基础上加了一个正则化项（Regularizer）

该方法在 BP 神经网络中仍然适用，对于给定的容量为 $N$ 的样本集 $D=\{(\mathbf{x}_1,\mathbf{y}_1),(\mathbf{x}_2,\mathbf{y}_2),…,(\mathbf{x}_N,\mathbf{y}_N)\}$，第 $i$ 组样本中的输入 $\mathbf{x}_i$ 具有 $n$ 个特征值，即：$\mathbf{x}_i=(x_i^{(1)},x_i^{(2)},…,x_i^{(n)})\in \mathbb{R}^n$，输出 $\mathbf{y}_i$ 具有 $m$ 个特征值，即：$\mathbf{y}_i=(y_i^{(1)},y_i^{(2)},…,y_i^{(m)})\in\mathcal{Y}=\mathbb{R}^{m}$

假设存在一具有 $n_l$ 层的神经网络，各层神经元个数为 $S_1=n,S_2,S_3,\cdots,S_{n_l}=m$，对于样本集中的第 $k$ 个样本 $(\mathbf{x}_k,\mathbf{y}_k)$，其通过神经网络的输出为 $\hat{\mathbf{y}}_k=(\hat{y_k}^{(1)},\hat{y_k}^{(2)},…,\hat{y_k}^{(m)})$，那么平方损失函数为：

$$E_{k}= (\hat{\mathbf{y}}_k-\mathbf{y}_k)^2$$

为便于求导，对 $E_k$ 整体乘以 $\frac{1}{2}$，此时得到的函数为第 $k$ 个样本的损失函数，即：

$$E_k= \frac{1}{2}(\hat{\mathbf{y}}_k-\mathbf{y}_k)^2$$

进一步，考虑正则化，对于各连接权重矩阵 $W^{[l]}$，其 $L_2$ 范数被称为弗罗贝尼乌斯范数（Frobenius Norm），即：

$$||W^{[l]}||_F^2 = \sum_{i=1}^{S_l}\sum_{j=1}^{S_{l+1}} (w_{ij}^{[l]})^2 \\$$

因此对于容量为 $N$ 的样本集，其正则化后的损失函数为：

$$\begin{align*} J(w,b) &= \frac{1}{N}\sum_{k=1}^N E_k + \frac{\lambda}{2}\sum_{l=1}^{n_l-1}||W^{[l]}||_F^2 \\ &= \frac{1}{2N}\sum_{k=1}^N \sum_{j=1}^m(\hat{y}_k^{(j)}-y_k^{(j)})^2+ \frac{\lambda}{2}\sum_{l=1}^{n_l-1}\sum_{i=1}^{S_l}\sum_{j=1}^{S_{l+1}} (w_{ij}^{[l]})^2 \\ \end{align*}$$

其中，第一项是均方误差项（经验风险），第二项是正则项，$\lambda\geq 0$ 是用于调整两者之间关系的系数

【随机失活】

基本原理

随机失活（Dropout）是在训练神经网络时的一种技巧，其在训练过程中，对网络的每一层设定一个保留概率，即每一层的任一神经元都有一定的概率被随机删除，这相当于在隐藏单元中增加了噪声

需要注意的是，所谓的删除，并非真正意义上的删除，而是将该部分的神经元的激活函数的输出设为 $0$，让这些神经元不参与计算

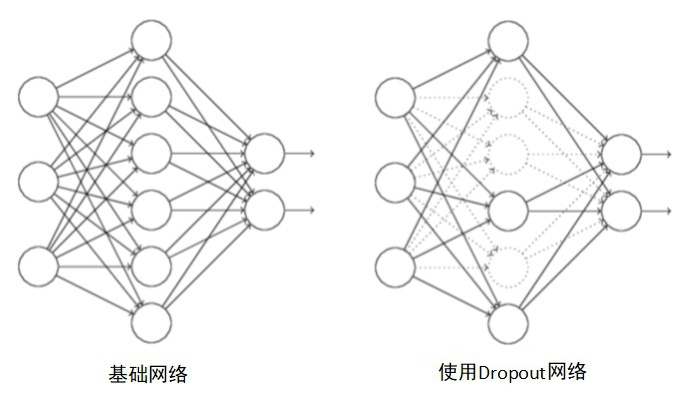
由于在训练过程中会产生不同的训练模型，而不同的训练模型也会产生不同的的计算结果，随着训练的不断进行，计算结果会在一个范围内波动，但是均值却不会有很大变化，因此可以把最终的训练结果看作是不同模型的平均输出

Dropout 消除、减弱了神经元节点间的联合，降低了网络对单个神经元的依赖，从而增强了泛化能力，进而防止了过拟合现象的出现

简单来说，在引入 Dropout 后，输入的特征都存在被随机清除的可能，所以神经元不会再特别依赖于任何一个输入特征，即不会给任何一个输入特征设置太大的权重

实现

Dropout 通常对会每层进行如下的代码操作：

# 假设设置神经元保留概率
keep_prob = 0.8
# 为第 l 层随机建立一个标记 1 或 0 的 Dropout 矩阵，表示随机失活的单元，占比 1-keep_prob
D_l = np.random.rand(A_l.shape[0], A_l.shape[1]) < keep_prob
# 将标记矩阵与第 l 层的输出值 A_l 相乘，使得 A_l 对应 D_l 的为 0 地方结果为 0
A_l = np.multiply(A_l, D_l)
# 对输出值乘以 1/p
A_l /= keep_prob

对于如上代码，对于 BP 神经网络中第 $l$ 层的权重累计 $Z^{[l]}=W^{[l-1]}A^{[l-1]}+\mathbf{b}^{[l-1]}$，保留概率为 $p=0.8$，当 $l-1$ 层存在比例为 $1-p=0.2$ 的单元被删除后，第 $l-1$ 层的输出值 $A^{[l-1]}$ 大约会变为原来的 $80\%$，而为了保证第 $l$ 层的权重累计 $Z^{[l]}$ 的均值不变，因此要将 $l-1$ 层的输出值 $A^{[l-1]}$ 与 Dropout 矩阵 $D^{[l]}$ 相乘后的权重进行扩大，即乘以 $\frac{1}{p}$

举例来说，假设第 $l$ 层存在 $10$ 个神经元，第 $l$ 层的权重累计 $Z^{[l]}$ 的期望为：

$$\frac{1+1+1+1+1+1+1+1+1+1}{10} = 1$$

保留概率为 $p=0.8$，那么现在有 $20\%$ 的神经元失效，此时均值变为 $0.8$，而为保证均值不变，因此要乘以 $\frac{10}{8}$，即：

$$0.8 * \frac{10}{8} = 1$$

通过传播过程，Dropout 将产生和 $L2$ 正则化相同的收缩权重的效果，对于不同的层，保留概率的大小设定也不一致，通常来说，对于神经元较少的层，保留概率常设为 $1$，而对于神经元较多的层，则会设置较小的保留概率

此外，由于 Dropout 每次会随机消除一部分神经元，所以参数也无法确定具体哪些，这在反向传播的时候会带来计算上的麻烦，也无法保证当前网络的损失函数是否是下降的

因此，如果要使用 Droupout，通常会先关闭这个参数，在保证损失函数是单调下降，确定网络没有问题后，再次打开 Droupout

【早停止】

早停止（Early Stopping）是一种使用截断迭代次数以防止过拟合的方法，常用于学习过程中存在迭代的学习方法

通常来说，在训练验证的时候，发现过拟合，可以得到如下的损失图

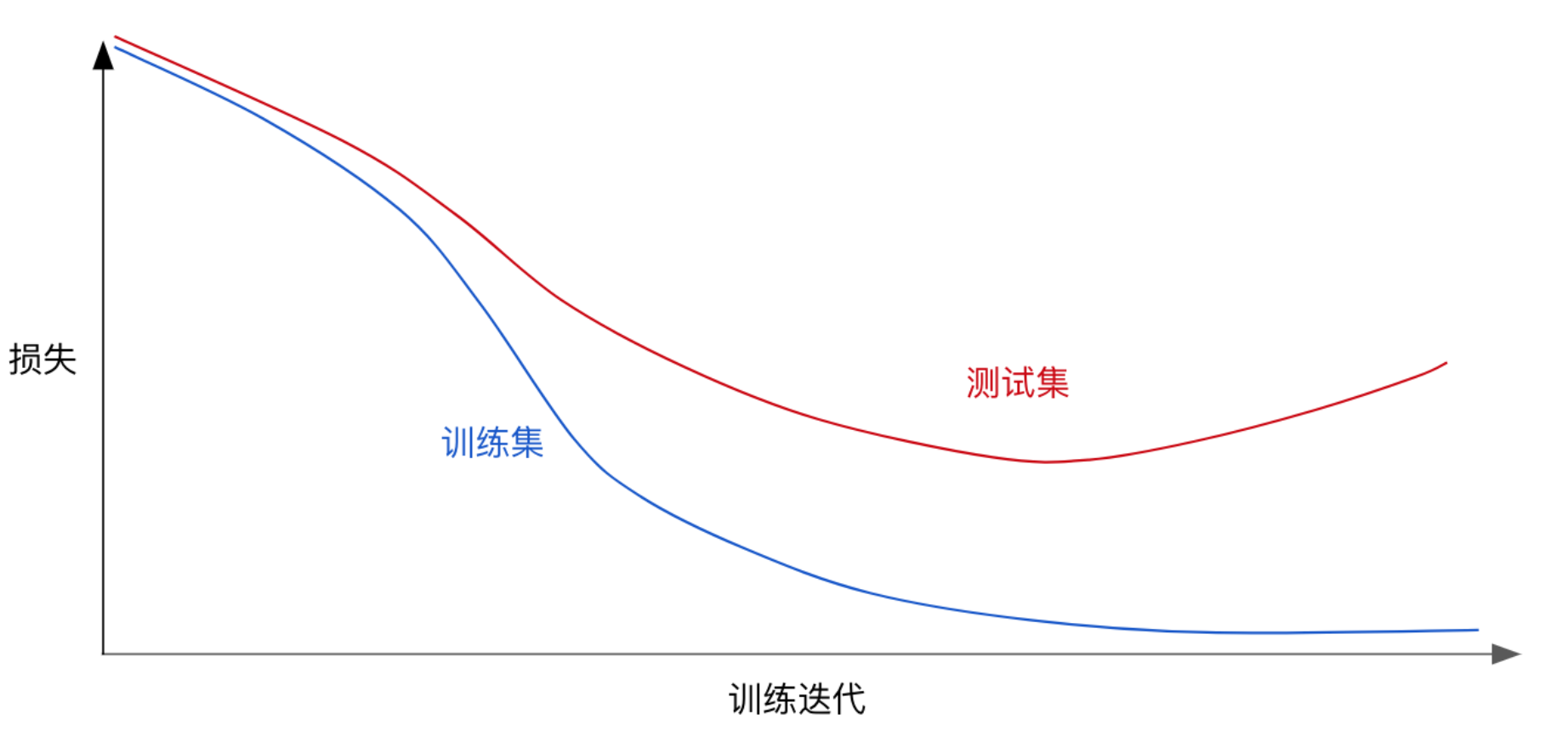
从图中可以看出，在不断训练之后，损失会越来越小，但是到了一定程度后，学习到的模型过于复杂，即过于拟合训练集上的数据的特征，从而造成测试集开始损失较小，后来又变大的情况

那么在模型对训练集迭代收敛前，发现测试集的损失减小到一定程度时，即可停止训练，从而防止过拟合

但早停止这种方法治标不治本，没有从根本上解决数据或模型的问题

【数据增强】

数据增强（Data Augmentation）是一种数据扩充技术，其通过剪切、旋转、反射、翻转变换、缩放变换、平移变换、尺度变换、对比度变换、噪声扰动、颜色变换等手段对原数据集进行变换，从而扩充数据集

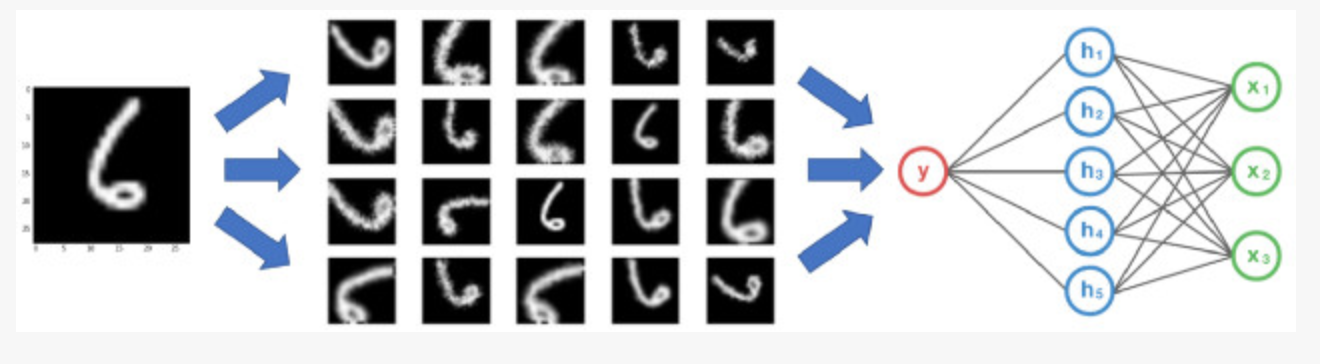
关于数据增强的详细介绍，见：数据增强