局部最优问题与鞍点问题

【局部最优问题】

在求解最优化问题时，凸优化问题有全局最优解与局部最优解的区别

全局最优是指求一个问题在全值域范围内最优，局部最优是指一个问题的解在一定范围或区域内最优，或者说解决问题或达成目标的手段在一定范围或限制内最优

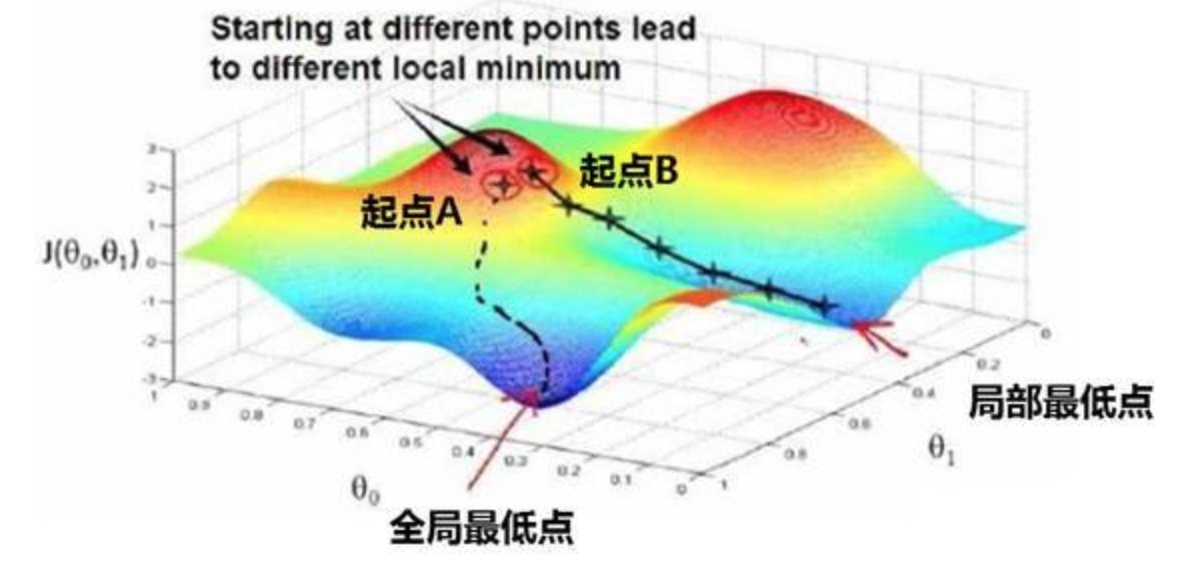
在优化神经网络的参数时，梯度下降法或者某个算法可能困在一个局部最优中，而不会抵达全局最优

【鞍点问题】

鞍点（Saddle）是函数上的导数为零，但不是函数局部极值的点

在训练较大的神经网络时，存在大量参数，且代价函数被定义在较高的维度空间时，困在极差的局部最优解的情况基本不会出现，但鞍点附近的平稳段会使得学习非常缓慢，甚至会困在鞍点附近

【解决方案】

解决方式

对于局部最优解问题和鞍点问题，有多种解决方式，通常各方式会结合使用：

1. 初始化参数策略
2. 小批量梯度下降法
3. 梯度下降法的优化算法
4. 学习率衰减

初始化参数策略

对于 BP 神经网络，采取如下的符号假设：

1. 用 $w_{ij}^{[l]}$ 表示第 $l$ 层的第 $i$ 个神经元与第 $l+1$ 层的第 $j$ 个神经元的连接权重
2. 用 $b_{i}^{[l]}$ 表示第 $l$ 层的第 $i$ 个神经元的偏置项（激活阈值）
3. 用 $z_{i}^{[l]}$ 表示第 $l$ 层的第 $i$ 个神经元的权重累计
4. 用 $a_i^{[l]}$ 表示第 $l$ 层的第 $i$ 个神经元的激活值（输出值）

对于第 $L_l$ 层第 $i$ 个神经元的累计权重 $z_{i}^{[l]}$，有：

$$z_i^{[l]} = w_{1i}^{[l-1]}a_1^{[l-1]}+w_{2i}^{[l-1]}a_2^{[l-1]}+\cdots+w_{ni}^{[l-1]}a_n^{[l-1]}+b_i^{[l-1]}$$

当神经元数量 $n$ 极大时，即使每个连接权重 $w_{ij}^{[l]}$ 都略小一些，但最终加和得到的 $z_{i}^{[l]}$ 也会非常大，在经过激活函数后，梯度较小，极容易出现鞍点问题

初始化参数策略是最简单的一种策略，其会将各层的连接权重 $w_{ij}^{[l]}$ 初始化为一极小的值，使得权重累计 $z_i^{[l]}$ 所得到的值趋近于 $0$

这样在使用 sigmoid 函数或 tanh 作为激活函数时，梯度较大，能够提高算法的更新速度

小批量梯度下降法

在对神经网络的参数进行优化时，可以采用小批量梯度下降法来代替随机梯度下降，其相对来说噪声较低，且损失函数总是向减小的方向下降

选择一个合适大小的 batch 进行小批量梯度下降，在数据量较大的网络中，可以明显地减少梯度计算的时间

关于小批量梯度下降法，详见：梯度下降法

梯度下降法的优化算法

除了小批量梯度下降法外，还有一些对梯度下降法内部梯度下降过程进行优化的算法，这些算法比梯度下降法的速度更快，效果也更好

• 动量梯度下降法：计算梯度的指数加权平均数，并利用该值来更新参数值
• RMSProp 算法：对梯度进行指数加权平均的基础上，引入平方和平方根
• Adam 算法：动量梯度下降法与 RMSProp 算法的结合

关于以上三个算法的详细介绍，详见：梯度下降法的优化算法

不同优化算法的对比效果图如下

学习率衰减

如果设置一个固定的学习率 $\alpha$，那么在最小值点附近，由于不同的数据存在一定的噪声，因此不会精确收敛，而是会始终在最小值周围的一个较大范围内波动

但如果令学习率 $\alpha$ 随着时间缓慢减小，这样在初期 $\alpha$ 较大时，下降的步长比较大，能以较快的速度进行梯度下降，在后期 $\alpha$ 较小时，下降的步长较小，能够帮助算法收敛，更容易接近最优解

这种令学习率 $\alpha$ 随时间缓慢减小的策略即学习率衰减，最常用的学习率衰减方法为：

$$\alpha = \frac{1}{1+\text{decay_rate} * \text{epoch_num}} * \alpha_0$$

其中，$\text{decay_rate}$ 为衰减率，其是一个超参数，$\text{epoch_num}$ 是总循环轮次

此外，还有一种指数衰减的方式，即：

$$\alpha = 0.95^{\text{epoch_num}} * \alpha$$

对于大型的网络结构来说，可以采用学习率衰减这种方式来自动调整学习率，而一些小型网络直接手动调整即可