【概述】

非负矩阵分解（Non-negative Matrix Factorization，NMF）是由 Lee 和 Seung 于 1999 年在《Nature》上提出的一种矩阵分解方法，其使分解后的所有分量均为非负值，并且同时实现非线性的维数约减，NMF 目前已逐渐成为机器学习中常用的多维数据处理工具之一

【基本思想】

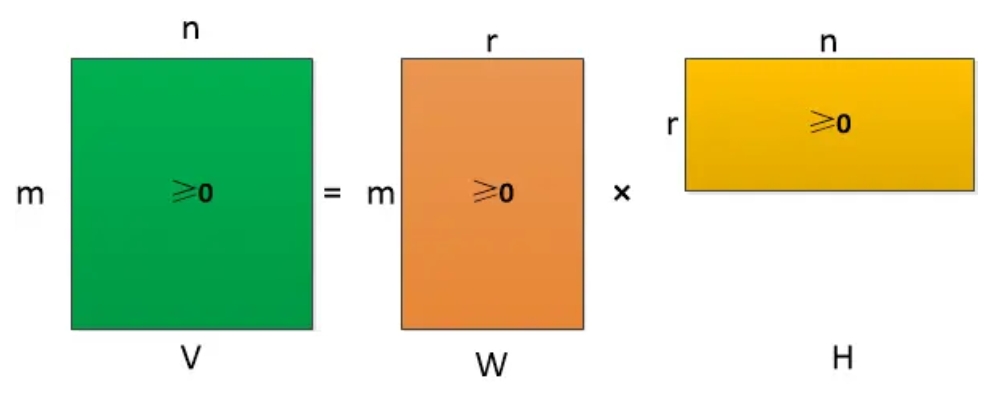
非负矩阵分解是指，对于一个给定的非负矩阵 $V\geq 0$，找到两个非负矩阵 $W\geq 0$ 和 $H\geq 0$，使得：

$V\approx WH$

即将非负矩阵 $V$ 分解为两个非负矩阵 $W$ 和 $H$ 的乘积的形式，由于 $V$ 和 $WH$ 完全相等很难实现，因此只要求两者近似相等

假设非负矩阵 $V$ 是 $m\times n$ 矩阵，非负矩阵 $W$ 和 $H$ 分别为 $m\times r$ 和 $r\times n$ 矩阵，同时 $r<\min(m,n)$，即 $W$ 和 $H$ 小于原始矩阵 $V$，因此非负矩阵分解可以看作是对原数据的压缩

根据上述的近似式可知，矩阵 $V$ 的第 $j$ 列向量 $\mathbf{v}_j$ 满足：

$\begin{align*} \mathbf{v}_j &\approx W\mathbf{h}_j \\ &= \begin{bmatrix} \mathbf{w}_1 & \mathbf{w}_2 & \cdots & \mathbf{w}_r \end{bmatrix} \begin{bmatrix} h_{1j} \\ h_{2j} \\ \vdots \\ h_{rj} \end{bmatrix} \\ &= \sum_{k=1}^r h_{kj} \mathbf{w}_k, \quad j=1,2,\cdots,n \end{align*}$

其中，$\mathbf{w}_k$ 是矩阵 $W$ 的第 $k$ 列，$\mathbf{h}_j$ 是矩阵 $H$ 的第 $j$ 列，$h_{kj}$ 是 $\mathbf{h}_j$ 上的第 $k$ 个元素，$k=1,2,\cdots,r$

上式表明，矩阵 $V$ 的第 $j$ 列 $\mathbf{v}_j$ 可以由矩阵 $W$ 的 $k$ 个列 $\mathbf{w}_k$ 的线性组合逼近，线性组合的系数是矩阵 $H$ 的第 $j$ 列 $\mathbf{h}_{j}$ 的元素，也就是说，矩阵 $W$ 的列向量为一组基，矩阵 $H$ 的列向量为线性组合系数，因此称 $W$ 为基矩阵，$H$ 为系数矩阵

【非负矩阵分解的形式化】

损失函数

设两个非负矩阵 $A=[a_{ij}]_{m\times n}$ 和 $B=[b_{ij}]_{m\times n}$，非负矩阵分解的平方损失函数可以定义为：

$\Vert A-B \Vert^2 = \sum_{i,j} (a_{ij}-b_{ij})^2$

其下界为 $0$，当且仅当 $A=B$ 时达到下界

非负矩阵分解的另一种损失函数是散度（Divergence），散度损失函数定义为：

$D(A\Vert B) = \sum_{i,j}(a_{ij}\log \frac{a_{ij}}{b_{ij}}-a_{ij}+b_{ij})$

其下界也是 $0$，当且仅当 $A=B$ 时达到下界，当 $\sum\limits_{i,j}a_{ij} = \sum\limits_{i,j} b_{ij}=1$ 时，散度损失函数退回为 KL 散度或相对熵，此时 $A$ 和 $B$ 是概率分布

最优化问题

当采用平方损失函数时，目标函数 $\Vert V-WH \Vert^2$ 关于基矩阵 $W$ 和系数矩阵 $H$ 的最小化，满足约束条件 $W,H\geq 0$，即：

$\begin{gather*} \min_{W,H} & \Vert V-WH \Vert^2 \\ s.t. &W,H \geq 0 \end{gather*}$

当采用散度损失函数时，目标函数 $D(V\Vert WH)$ 关于基矩阵 $W$ 和系数矩阵 $H$ 的最小化，满足约束条件 $W,H\geq 0$，即：

$\begin{gather*} \min_{W,H} & D(V\Vert WH) \\ s.t. &W,H \geq 0 \end{gather*}$

【基于乘法更新规则的优化算法】

概述

对于上述的两个最优化问题，由于目标函数 $\Vert V-WH \Vert^2$ 和 $D(V\Vert WH)$ 只是对变量 $W$ 和 $H$ 之一的凸函数，而不是同时对两个变量的凸函数，找到全局最小值较为困难，因此可以通过数值最优化方法求局部最优极小值

采用梯度下降法容易实现，但收敛速度较慢，共轭梯度法收敛速度快，当实现较为复杂，为此 Lee 和 Seung 提出了基于乘法更新规则的优化算法，交替地对 $W$ 和 $H$ 进行更新

乘法更新规则

平方损失 $\Vert V-WH \Vert^2$ 对下列乘法更新规则是非增的，当前仅当 $W$ 和 $H$ 是平方损失函数的稳定点时函数的更新不变

$\begin{gather*} H_{kj} \leftarrow H_{kj} \frac{(W^TV)_{kj}}{(W^TWH)_{kj}} \\ W_{ik} \leftarrow W_{ik} \frac{(VH^T)_{ik}}{(WHH^T)_{ik}} \end{gather*}$

散度损失 $D(V\Vert WH)$ 对下列乘法更新规则是非增的，当前仅当 $W$ 和 $H$ 是散度损失函数的稳定点时函数的更新不变

$\begin{gather*} H_{kj} \leftarrow H_{kj} \frac{\sum\limits_{i}\frac{W_{ik}V_{ij}}{(WH)_{ij}}}{\sum\limits_i W_{ik}} \\ W_{ik} \leftarrow W_{ik} \frac{\sum\limits_{j}\frac{H_{kj}V_{ij}}{(WH)_{ij}}}{\sum\limits_j H_{kj}} \end{gather*}$

算法

下面仅讨论平方损失函数的非负矩阵分解算法，散度损失函数的非负矩阵分解算法与其相似，不再进行赘述

对于最优化的目标函数 $\Vert V-WH \Vert^2$，首先将目标函数乘以 $\frac{1}{2}$ 以便于后续化简，其最优解与原始问题相同，即：

$J(W,H) = \frac{1}{2} \Vert V-WH \Vert^2 = \frac{1}{2} \sum [V_{ij} - (WH)_{ij}]^2$

使用梯度下降法进行求解，对于目标函数，其梯度为：

$\begin{align*} \frac{\partial J(W,H)}{\partial W_{ik}} &= -\sum_{j} [V_{ij}-(WH)_i] H_{kj} \\ &= -[(VH^T)_{ik} - (WHH^T)_{ik}] \end{align*}$

同理，可得：

$\frac{\partial J(W,H)}{\partial H_{kj}} = -[(W^TV)_{kj} - (W^TWH)_{kj}]$

然后求得梯度下降法的更新规则，即有：

$\begin{gather*} W_{ik} = W_{ik} + \lambda_{ik}[(VH^T)_{ik}-(WHH^T)_{ik}] \\ H_{kj} = H_{kj} + \mu_{kj}[(W^TV)_{kj}-(W^TWH)_{kj}] \end{gather*}$

其中，$\lambda_{ik},\mu_{kj}$ 是步长

.选取：

$\lambda_{ik}=\frac{W_{ik}}{(WHH^T)_{ik}},\quad \mu=\frac{H_{kj}}{(W^TWH)_{kj}}$

即得乘法更新规则：

$\begin{gather*} W_{ik} = W_{ik} \frac{(VH^T)_{ik}}{(WHH^T)_{ik}},\quad i=1,2,\cdots,m;k=1,2,\cdots,r \\ H_{kj} = W_{ik} \frac{(W^TV)_{kj}}{(W^TWH)_{kj}},\quad j=1,2,\cdots,n;k=1,2,\cdots,r \end{gather*}$

只要基矩阵 $W$ 和系数矩阵 $H$ 初始选取时为非负矩阵，就可以保证迭代过程及结果的基矩阵 $W$ 和系数矩阵 $H$ 均为非负

算法流程

输入：非负矩阵 $V$，最大迭代次数 $t$，要压缩到的维度 $r$

输出：基矩阵 $W$ 和系数矩阵 $H$

Step 1：初始化。随机选取两个非负矩阵，作为基矩阵 $W$ 和系数矩阵 $H$ 的初始矩阵

Step2：迭代。对迭代次数从 $1$ 到 $t$，更新基矩阵 $W$ 和系数矩阵 $H$