潜在语义分析 LSA

【概述】

潜在语义分析（Latent Semantic Analysis，LSA）直观上就是将文本在单词向量空间的表示 $X$ 通过线性变换转换为在话题向量空间中的表示 $Y$

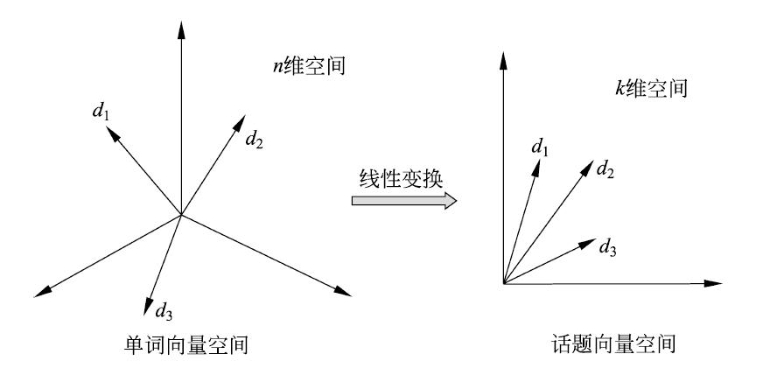
在原始的单词向量空间中，两个文本 $d_i$ 和 $d_j$ 的相似度可由对应向量 $\mathbf{x}_i,\mathbf{x}_j$ 的度量表示，经过潜在语义分析后，在话题向量空间中，两个文本 $d_i$ 和 $d_j$ 的相似度可由对应向量 $\mathbf{y}_i,\mathbf{y}_j$ 的度量表示

【单词向量空间到话题向量空间的线性变换】

对于一个含有 $n$ 个文本的集合 $D=\{d_1,d_2,\cdots,d_n\}$，以及在所有文本中出现的 $m$ 个单词的集合 $W=\{w_1,w_2,\cdots,w_m\}$，其单词-文本矩阵为：

$$X = \begin{bmatrix} x_{11} & x_{12} & \ldots & x_{1n}\\ x_{21} & x_{22} & \ldots & x_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ x_{m1} & x_{m2} & \ldots & x_{mn}\\ \end{bmatrix} = \begin{bmatrix} \mathbf{x}_{1} & \mathbf{x}_{2} & \ldots & \mathbf{x}_{n} \end{bmatrix}$$

其中，元素 $x_{ij}$ 表示为单词 $w_i$ 在文本 $d_j$ 中出现的频数或权值

假设所有文本共含有 $K$ 个话题，那么对应的单词-话题矩阵为：

$$T = \begin{bmatrix} t_{11} & t_{12} & \ldots & t_{1K}\\ t_{21} & t_{22} & \ldots & t_{2K}\\ \vdots & \vdots & \ddots & \vdots\\ t_{m1} & t_{m2} & \ldots & t_{mK}\\ \end{bmatrix} = \begin{bmatrix} \mathbf{t}_{1} & \mathbf{t}_{2} & \cdots & \mathbf{t}_{K} \end{bmatrix}$$

其中，$t_{ik}$ 是单词 $w_i$ 在话题 $\mathbf{t}_k$ 上的权值

矩阵 $X$ 投影到话题向量空间 $T$ 中的话题-文本矩阵为：

$$Y = \begin{bmatrix} y_{11} & y_{12} & \ldots & y_{1n}\\ y_{21} & y_{22} & \ldots & y_{2n}\\ \vdots & \vdots & \ddots & \vdots\\ y_{K1} & y_{K2} & \ldots & y_{Kn}\\ \end{bmatrix} = \begin{bmatrix} \mathbf{y}_{1} & \mathbf{y}_{2} & \cdots & \mathbf{y}_{n} \end{bmatrix}$$

其中，$y_{jk}$ 是文本 $d_j$ 在话题 $\mathbf{t}_k$ 上的权值

此时，对于单词向量空间的文本向量 $\mathbf{x}_j$ 可通过它在话题向量空间中的投影向量 $\mathbf{y}_j$ 近似表示，即由 $K$ 个话题向量以 $\mathbf{y}_j$ 为系数的线性组合近似表示

$$\mathbf{x}_j \approx y_{1j}\mathbf{t}_1 + y_{2j}\mathbf{t}_2 + \cdots + y_{Kj}\mathbf{t}_K, \quad i=1,2,\cdots,n$$

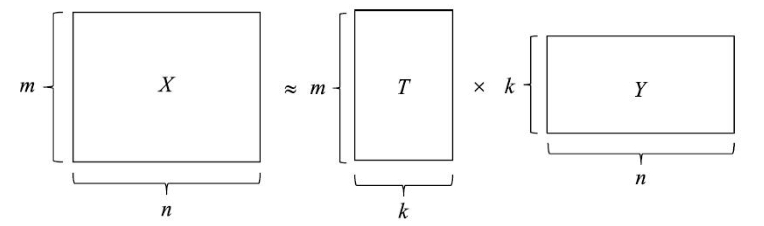
也就是说，单词文本矩阵 $X$ 即可近似的表示为话题文本矩阵 $Y$ 与单词话题矩阵 $T$ 的乘积形式，这就是潜在语义分析

$$X\approx TY$$

可以发现，要进行潜在语义分析，需要同时决定两部分的内容：话题向量空间 $T$、文本在话题向量空间中的表示 $Y$，使两者的乘积是原始单词-文本矩阵 $X$ 的近似

【奇异值分解算法】

潜在语义分析模型

利用矩阵奇异值分解算法，可以实现潜在语义分析，具体来说，将单词-文本矩阵 $X$ 进行奇异值分解，其中左矩阵作为话题向量空间 $T$，对角矩阵与右矩阵的乘积作为文本在话题向量空间的表示 $Y$，即：

$$X\approx U_K\Sigma_KV_K^T = U_K(\Sigma_KV_K^T)$$

其中，话题空间 $T= U_K$，文本在话题空间中的表示 $Y=\Sigma_KV_K^T$​

关于奇异值分解的原理与算法，详见：矩阵的奇异值分解，这里不再赘述

话题向量空间

$$X \approx U_K\Sigma_KV_K^T = \begin{bmatrix} \mathbf{u}_1 & \mathbf{u}_2 & \cdots & \mathbf{u}_K \end{bmatrix} \begin{bmatrix} \sigma_1 & 0 & \cdots & 0 \\ 0 & \sigma_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma_K\\ \end{bmatrix}\begin{bmatrix} \mathbf{v}_1^T \\ \mathbf{v}_2^T \\ \vdots \\ \mathbf{v}_K^T \end{bmatrix},\quad K\leq n \leq m$$

其中，矩阵 $U_K$ 的每一个列向量 $\mathbf{u}_k=\begin{bmatrix}u_{1k}\\u_{2k}\\\vdots\\u_{mk}\end{bmatrix},k=1,2,\cdots,K$ 表示一个话题，即话题向量，由这 $K$ 个话题向量张成的子空间即为话题向量空间

文本在话题空间

进一步，考虑文本在话题向量空间的表示，将上式进行展开，有：

$$\begin{align*} X &\approx U_K\Sigma_KV_K^T \\ &= \begin{bmatrix} \mathbf{u}_1 & \mathbf{u}_2 & \cdots & \mathbf{u}_K \end{bmatrix} \begin{bmatrix} \sigma_1 & 0 & \cdots & 0 \\ 0 & \sigma_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \sigma_K\\ \end{bmatrix}\begin{bmatrix} v_{11} & v_{21} & \cdots & v_{n1} \\ v_{12} & v_{22} & \cdots & v_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ v_{1K} & v_{2K} & \cdots & v_{nK}\\ \end{bmatrix} \\ &= \begin{bmatrix} \mathbf{u}_1 & \mathbf{u}_2 & \cdots & \mathbf{u}_K \end{bmatrix}\begin{bmatrix} \sigma_{1} v_{11} & \sigma_{1}v_{21} & \cdots & \sigma_{1}v_{n1} \\ \sigma_{2}v_{12} & \sigma_{2}v_{22} & \cdots & \sigma_{2}v_{n2} \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{k}v_{1K} & \sigma_{k}v_{2K} & \cdots & \sigma_{K}v_{nK}\\ \end{bmatrix} \\ \end{align*}$$

此时，矩阵 $X$ 的第 $j$ 列向量 $\mathbf{x}_j$ 即为文本 $d_j$ 的近似表达式，由 $K$ 个话题向量 $\mathbf{u}_k$ 的线性组合构成，即：

$$\begin{align*} \mathbf{x}_j &\approx U_K(\Sigma_K V_K^T)_j \\ &= \begin{bmatrix} \mathbf{u}_1 & \mathbf{u}_2 & \cdots & \mathbf{u}_K \end{bmatrix}\begin{bmatrix} \sigma_{1}v_{j1} \\ \sigma_{2}v_{j2} \\ \vdots \\ \sigma_{K}v_{jK} \end{bmatrix} \\ &= \sum_{k=1}^K \sigma_k v_{jk} \mathbf{u}_{k} ,\quad j=1,2,\cdots,n \end{align*}$$

其中，$(\Sigma_KV_K^T)_j$ 是矩阵 $\Sigma_KV_K^T$ 的第 $j$ 列向量

对于矩阵 $\Sigma_KV_K^T$ 的每一个列向量：

$$\begin{bmatrix} \sigma_{1}v_{11} \\ \sigma_{2}v_{12} \\ \vdots \\ \sigma_{k}v_{1K} \end{bmatrix},\begin{bmatrix} \sigma_{1}v_{21} \\ \sigma_{2}v_{22} \\ \vdots \\ \sigma_{k}v_{2K} \end{bmatrix},\cdots,\begin{bmatrix} \sigma_{1}v_{n1} \\ \sigma_{2}v_{n2} \\ \vdots \\ \sigma_{k}v_{nK} \end{bmatrix}$$

都是一个文本在话题向量空间的表示

【非负矩阵分解算法】

利用非负矩阵分解的算法，也可以实现潜在语义分析，具体来说，将单词-文本矩阵 $X$ 进行非负矩阵分解，其中左矩阵作为话题向量空间 $T$，右矩阵作为文本在话题向量空间的表示 $Y$，需要注意的是，这要求单词-文本矩阵是非负的

对于给定的 $m\times n$ 维的非负单词-文本矩阵 $X\geq 0$，假设文本集合 $D=\{d_1,d_2,\cdots,d_n\}$ 中共包含 $K$ 个话题，对 $X$ 进行非负矩阵分解，即求非负的 $m\times K$ 矩阵 $W\geq 0$ 和 $K\times n$ 矩阵 $H\geq 0$，使得：

$$X\approx WH$$

矩阵 $W=[\mathbf{w}_1,\mathbf{w}_2,\cdots,\mathbf{w}_K]$ 即为话题向量空间 $T$，向量 $\mathbf{w}_k$ 即文本集合中的第 $k$ 个话题，矩阵 $H=[\mathbf{h}_1,\mathbf{h}_2,\cdots,\mathbf{h}_n]$ 即文本在话题向量空间的表示 $Y$，向量 $\mathbf{h}_i$ 即文本集合中的第 $i$ 个文本

关于非负矩阵分解的原理与算法，详见：非负矩阵分解，这里不再赘述