【概述】

概率潜在语义分析（Probabilistic Latent Semantic Analysis，PLSA）也称概率潜在语义索引（Probabilistic Latent Semantic Indexing，PLSI），是一种利用概率生成模型对文本集合进行话题分析的无监督学习方法

PLSA 受 LSA 启发，由 Hofmann 于 1999 年提出，与 LSA 不同的是，LSA 基于非概率模型，PLSA 基于概率模型，其假设每个文本由一个话题分布决定，每个话题由一个单词分布决定，利用隐变量表示话题，整个模型表示为一个由文本生成话题、话题生成单词，进而得到单词-文本共现数据的过程

对于一个给定的文本集合，每个文本包含若干话题，每个话题由若干单词表示，话题是潜在的，一个话题表示一个语义内容，无法从文本集合中的数据直接观察到，对文本集合进行 PLSA 就能够发现每个文本的话题以及每个话题的单词，即从文本集合中发现由隐变量表示的话题，即潜在语义（Latent Semantic）

如下图所示，每一行对应一个单词，每一列对应一个文本，每一个元素表示单词在文本中出现的次数，红、绿、蓝框各自表示一个话题

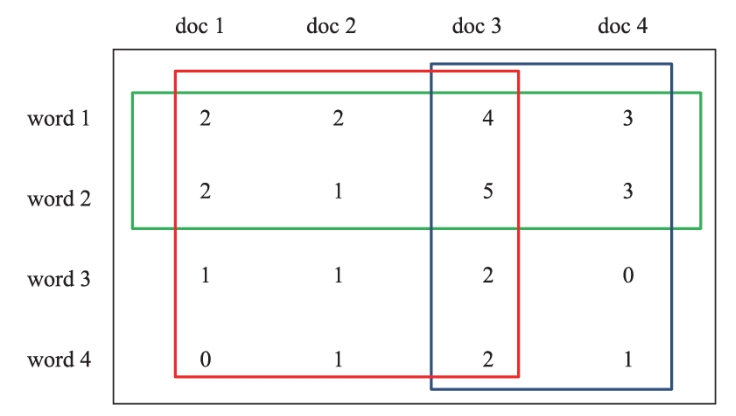
【生成模型与共现模型】

生成模型

对于一个含有 $N$ 个文本的文本集合 $D=\{d_1,d_2,\cdots,d_N\}$，以及在所有文本中出现的 $M$ 个单词的集合 $W=\{w_1,w_2,\cdots,w_M\}$，假设文本集合中共存在 $K$ 个话题，话题集合为 $Z=\{z_1,z_2,\cdots,z_K\}$

从文本集合 $D$ 中取随机变量 $d$，从单词集合 $W$ 中取随机变量 $w$，从话题集 $Z$ 中取随机变量 $z$，概率分布 $P(d)$、条件概率 $P(z|d)$、条件概率分布 $P(w|z)$ 均属于多项分布，其中，$P(d)$ 表示生成文本 $d$ 的概率，$P(z|d)$ 表示文本 $d$ 生成话题 $z$ 的概率，$P(w|z)$ 表示话题 $z$ 生成单词 $w$ 的概率

由于每个文本的内容由其相关话题决定，每个话题的内容由其相关单词决定，也就是说每个文本 $d$ 拥有自己的话题概率分布 $P(z|d)$，每个话题 $z$ 拥有自己的单词概率分布 $P(w|z)$

生成模型假设在话题 $z$ 给定的条件下，单词 $w$ 与文本 $d$ 条件独立，即：

$P(w,z|d) = P(z|d) P(w|z)$

生成模型通过以下步骤生成文本-单词共现数据：

依据概率分布 $P(d)$，从文本集合中随机选取一个文本 $d$，共生成 $N$ 个文本，针对每个文本，执行 2
在文本 $d$ 给定的条件下，依据条件概率分布 $P(z|d)$，从话题集合中随机选取一个话题 $z$，共生成 $L$ 个话题，$L$ 为文本长度，针对每个话题，执行 3
在话题 $z$ 给定的条件下，依据条件概率分布 $P(w|z)$，从单词集合中随机选取一个单词 $w$

生成模型中，文本变量 $d$ 与单词变量 $w$ 是观测变量，话题变量 $z$ 是隐变量，即模型生成的是单词-话题-文本三元组 $(w,z,d)$ 的集合，但观测到的是单词-文本 $(w,d)$ 的集合，观测数据表示为单词-文本矩阵 $T$ 的形式，矩阵的行表示单词，列表示文本，元素表示单词-文本对 $(w,d)$ 的出现次数

从数据的生成过程可以推出，文本-单词共现数据 $T$ 的生成概率为所有单词-文本对 $(w,d)$ 的生成概率的乘积，即

$P(T) = \prod_{(w,d)} P(w,d)^{n(w,d)}$

其中，$n(w,d)$ 为单词-文本对 $(w,d)$ 的出现次数

那么，单词-文本对出现的总次数是 $N\times L$，生成模型的即可定义为每个单词-文本对 $(w,d)$ 的生成概率，即：

$\begin{align*} P(w,d) &= P(d) P(w|d) \\ &= P(d) \sum_{z} P(w,z|d) \\ &= P(d) \sum_{z} P(z|d) P(w|z) \end{align*}$

式中的单词变量 $w$ 和文本变量 $d$ 是非对称的，因此也称为非对称模型

生成模型属于概率有向图模型，可以用有向图表示，如下图所示，图中的实心圆表示观测变量，空心圆表示隐变量，箭头表示概率依存关系，方框表示多次重复，方框内的数字表示重复次数

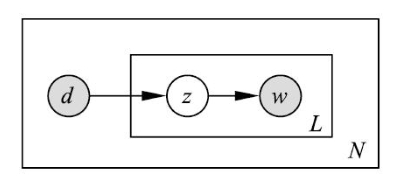
共现模型

可以定义与上述生成模型等价的共现模型，即对于文本-单词共现数据 $T$ 的生成概率为所有单词-文本对 $(w,d)$ 的生成概率的乘积

$P(T) = \prod_{(w,d)} P(w,d)^{n(w,d)}$

每个单词-文本对 $(w,d)$ 的概率由以下公式决定：

$P(w,d) = \sum_{x\in Z} P(z) P(w|z) P(d|z)$

式中的单词变量 $w$ 和文本变量 $d$ 是对称的，因此也称为对称模型

如下图所示，共线模型也可以使用有向图表示，图中的实心圆表示观测变量，空心圆表示隐变量，箭头表示概率依存关系，方框表示多次重复，方框内的数字表示重复次数

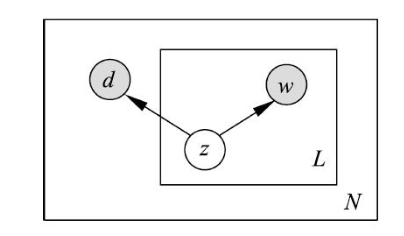
虽然生成模型和共现模型在概率公式意义上是等价的，但两者具有不同的性质，生成模型刻画的是文本-单词共现数据生成的过程，共现模型描述的是文本-单词共现数据拥有的模式

模型参数

对于 $N$ 个文本、$M$ 个单词、$K$ 个话题，如果直接定义单词与文本的共现概率 $P(w,d)$，模型参数的个数是 $O(M\cdot N)$，而生成模型和共现模型的参数个数是 $O(M \cdot K+ N\cdot K)$，在现实应用中 $K\ll M$，因此 PLSA 通过话题对数据进行了更简洁的表示，减少了学习过程中过拟合的可能性

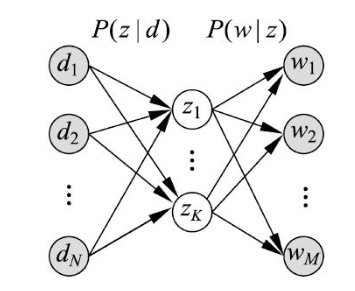
【与 LSA 的关系】

概率潜在语义分析模型（共现模型）可以在潜在语义分析模型的框架下描述

如下图所示，在 LSA 中对单词-文本矩阵可以通过奇异值分解得到 $X=U\Sigma V^T$，其中，$U,V$ 为正交矩阵，$\Sigma$ 为非负降序对角矩阵

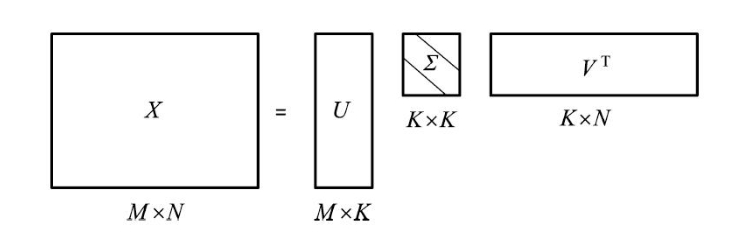
共现模型也可表示为三个矩阵的乘积的形式：

$\begin{align*} X' &= U'\Sigma' V'^T = [P(w,d)]_{M\times N}\\ X' &= [P(w|z)]_{M\times K} \\ \Sigma' &= [P(z)]_{K\times K} \\ V' &= [P(d|z)]_{N\times K} \end{align*}$

PLSA 中的矩阵 $U’,V’$ 是非负的、规范化的，表示概率分布，而 LSA 中的矩阵 $U,V$ 是正交的，未必非负，并不表示概率分布

【PLSA 的几何解释】

概率分布 $P(w|d)$ 表示文本 $d$ 生成单词 $w$ 的概率，可以由 $M$ 维空间的 $(M-1)$ 单纯形中的点表示，单纯形上的每个点表示一个分布 $P(w|d)$，所有的分布 $P(w|d)$ 都在单纯形上，称这个 $(M-1)$ 单纯形为单词单纯形（Word Simplex）

$\sum_{i=1}^M P(w_i|d) = 1, \quad 0\leq P(w_i|d)\leq 1, \quad i=1,2,\cdots,M$

根据生成模型：

$P(w,d) = P(d) \sum_{z} P(z|d) P(w|z)$

对于概率潜在语义分析模型（生成模型）的文本概率分布 $P(w|d)$ 有下面的关系成立：

$P(w|d) = \sum_{z} P(z|d) P(w|z)$

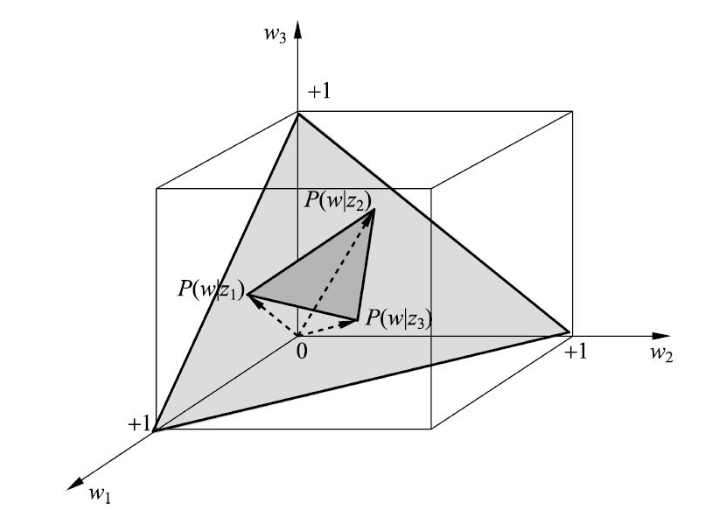
概率分布 $P(w|z)$ 表示话题 $z$ 生成单词 $w$ 的概率，其也存在于 $M$ 维空间中的 $(M-1)$ 单纯形中，如果有 $K$ 个话题，那么就有 $K$ 个概率分布 $P(w|z_k)$，由 $(M-1)$ 单纯形上的 $K$ 个点表示，以这 $K$ 个点为顶点，构成一个 $(K-1)$ 单纯形，称为话题单纯形（Topic Simplex），其是单词单纯形的子单纯形

如下图所示，为 $M=3,K=3$ 时生成模型的情况

【PLSA 的学习算法】

基本思想

概率潜在语义分析模型是含有隐变量的模型，其学习通常采用 EM 算法

给定单词-文本共现数据 $T=\{n(w_i,d_j)\},i=1,2\cdots,M,j=1,2,\cdots,N$，目标是概率潜在语义分析（生成模型）的参数

若使用极大似然估计，则对数似然函数为：

$\begin{align*} L &= \sum_{i=1}^M \sum_{j=1}^N n(w_i,d_j) \log P(w_i,d_j) \\ &= \sum_{i=1}^M \sum_{j=1}^N n(w_i,d_j) \log \Big[ P(w_i|z_k) P(z_k |d_j) \Big] \end{align*}$

但由于模型含有隐变量，对数似然函数的优化无法用解析方法求解，此时使用 EM 算法，应用 EM 算法的第一步是 E 步，即计算 Q 函数，其是完全数据的对数似然函数对不完全数据的条件分布的期望，即：

$Q = \sum_{k=1}^K \Bigg\{ \sum_{j=1}^N n(d_j) \Big[ \log P(d_j) + \sum_{i=1}^M \frac{n(w_i,d_j)}{n(d_j)} \log [P(w_i|z_k) P(z_k|d_j) ]\Big] \Bigg\} P(z_k|w_i,d_j)$

其中，$n(d_j)=\sum\limits_{i=1}^M n(w_i,d_j)$ 表示文本 $d_j$ 中的单词个数，$n(w_i,d_j)$ 表示单词 $w_i$ 在文本 $d_j$ 中出现的次数，条件概率分布 $P(z_k|w_i,d_j)$ 表示不完全数据，是已知变量，条件概率分布 $P(w_i|z_k)$ 和 $P(z_k|d_j)$ 的乘积代表完全数据，是未知变量

由于可以从数据中直接统计得出 $P(d_j)$ 的估计，因此只考虑 $P(w_i|z_k),P(z_k|d_j)$ 的估计即可，故而可将 Q 函数进行简化：

$Q'= \sum_{i=1}^M \sum_{j=1}^N n(w_i,d_j) \sum_{k=1}^K P(z_k|w_i,d_j) \log [P(w_i|z_k) P(z_k|d_j)]$

其中，$P(z_k|w_i,d_j)$ 可以根据贝叶斯公式计算，即：

$P(z_k|w_i,d_j) = \frac{P(w_i|z_k)P(z_k|d_j)}{\sum\limits_{k=1}^K P(w_i |z_k) P(z_k|d_j)}$

其中，$P(z_k|d_j),P(w_i|z_k)$ 可由 EM 算法的上一步迭代得到

在完成 EM 算法的 E 步：计算 Q 函数后，接着进行 EM 算法的 M 步：极大化 Q 函数

通过约束最优化求解 Q 函数的极大值，此时 $P(z_k|d_j),P(w_i|z_k)$ 形成概率分布，两者为变量，满足约束条件：

$\begin{gather*} \sum_{i=1}^M P(w_i|z_k) = 1, & k=1,2,\cdots,K \\ \sum_{k=1}^K P(z_k|d_j) = 1, & j=1,2,\cdots, N \end{gather*}$

应用拉格朗日法，引入拉格朗日乘子 $\tau_k,\rho_j$，定义拉格朗日函数：

$\Lambda = Q'+ \sum_{k=1}^K \tau_k \Big(1-\sum_{i=1}^M P(w_i|z_k)\Big) + \sum_{j=1}^N \rho_j \Big( 1-\sum_{k=1}^K P(z_k|d_j) \Big)$

将拉格朗日函数 $\Lambda$ 分别对 $P(w_i|z_k),P(z_k|d_j)$ 求偏导并令其等于 $0$，有：

$\begin{gather*} \sum_{j=1}^N n(w_i,d_j) P(z_k|w_i,d_j)-\tau_k P(w_i|z_k) =0 \\ \sum_{i=1}^M n(w_i,d_j) P(z_k|w_i,d_j)-\rho_j P(z_k|d_j) =0 \\ i=1,2,\cdots,M;\quad j=1,2,\cdots,M;\quad k=1,2,\cdots,K \end{gather*}$

解上述方程组，即可得到 M 步的参数估计式：

$\begin{gather*} P(w_i|z_k) = \frac{\sum\limits_{j=1}^N n(w_i,d_j)P(z_k|w_i,d_j)}{\sum\limits_{m=1}^M\sum\limits_{j=1}^N n(w_m,d_j)P(z_k|w_m,d_j)} \\ P(z_k|d_j) = \frac{\sum\limits_{i=1}^M n(w_i,d_j)P(z_k|w_i,d_j)}{n(d_j)} \end{gather*}$

算法流程

输入：含有 $N$ 个文本的文本集合 $D=\{d_1,d_2,\cdots,d_N\}$，在所有文本中出现的 $M$ 个单词的集合 $W=\{w_1,w_2,\cdots,w_M\}$，存在 $K$ 个话题的话题集合为 $Z=\{z_1,z_2,\cdots,z_K\}$，单词-文本共现数据 $T=\{n(w_i,d_j)\},i=1,2\cdots,M,j=1,2,\cdots,N$

输出：条件概率分布 $P(w_i|z_k)$ 和 $P(z_k|d_j)$

算法流程：

Step1：设置参数 $P(w_i|z_k)$ 和 $P(z_k|d_j)$ 的初始值

Step2：迭代执行以下 E 步、M 步，直到收敛为止

E 步：