【最大熵原理】
在 信息熵与互信息 中对信息熵进行了介绍,而最大熵原理,就是认为:在所有可能的概率分布中,熵最大的模型是最好的模型
对于来自参数空间 $\mathcal{X}$ 的离散随机变量 $X$,其概率分布为:
则信息熵为:
其取值范围为:
当 $X$ 只有一个分类时,信息熵取最小值 $H(X)=0$;而当 $X$ 的分布为均匀分布,即 $X$ 中 $n$ 个分类出现的概率相同时,信息熵取最大值 $H(X)=\log n$,此时 $p_i=\frac{1}{n}$
也就是说,所谓最大熵原理,就是在求解概率模型时,在满足约束条件的情况下,对于未知情况不做任何的主观假设,即将不确定部分视为等可能的,此时求得的模型为熵最大模型
【几何解释】
对于概率模型集合 $\mathcal{P}$,用欧式空间中的单纯形(Simplex)表示
具体来说,对于有 $k$ 个取值的离散型随机变量,使用 $k-1$ 维单纯形来表示,在单纯形中,一个点代表一个模型,整个单纯形代表了模型集合
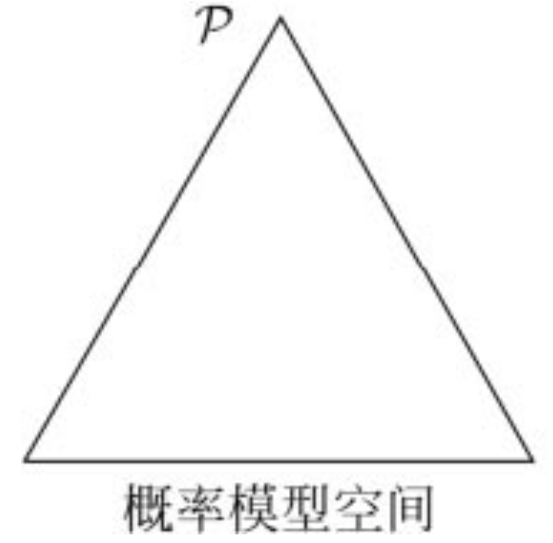
举例来说,假设随机变量 $X$ 其可能的取值有:$\{A,B,C\}$,将使用 2 维单纯形来表示随机变量 $X$,并将随机变量 $X$ 的三个取值 $A$、$B$、$C$ 设为 2 维单纯形的三个顶点
设单纯形中任意一点 $P$ 到三边距离和为 $1$(在正三角形中,恒等于三角形的高),点到边的距离为对应取值的概率
若给定概率 $P(A)=P(B)=P(C)=\frac{1}{3}$,则可用单纯形表示为:
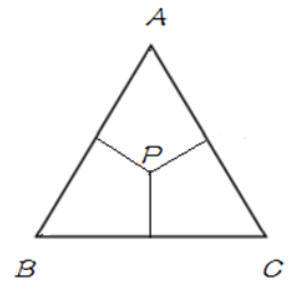
同理,若给定概率 $P(A)=1,P(B)=P(C)=0$,则可用单纯形表示为:

一条直线对应一个约束条件,直线的交集对应于满足所有约束条件的模型集合

学习的目的,就是在所有可能的模型集合中,选择最优模型,最大熵原理,给出了最优模型选择的一个准则
【实例】
举例来说,假设随机变量 $X$ 其可能的取值有:$\{A,B,C,D,E\}$,现在要估计其取各个值的概率 $P(A)$ 、$P(B)$ 、$P(C)$ 、$P(D)$ 、$P(E)$
已知的是,这些概率值满足以下约束条件:
满足这个约束条件的概率分布有无穷个,在没有任何信息的情况下,若仍要对概率分布进行估计,将 $X$ 的各取值的概率视为均等的,即:
此时,在等概率的情况下,熵最大
进一步,若给出了某些约束条件,则在给定约束条件的基础上,对其他缺少的未知信息的情况下,认为其他是等概率的
具体来说,在上例的基础上,给出了约束条件:
此时,可认为 $A$、$B$ 是等概率的, $C$、$D$、$E$ 是等概率的,即有:

