信息熵与互信息

Reference

• 信息熵是什么？ - D.Han的回答 - 知乎
• 信息熵公式的由来
• 互信息(Mutual Information)
• 详解机器学习中的熵、条件熵、相对熵和交叉熵
• 一文搞懂交叉熵在机器学习中的使用，透彻理解交叉熵背后的直觉
• 条件互信息的理解(Conditional Mutual Information)
• 条件互信息

【信息熵】

信息熵

定义

熵（Entropy）最早是由物理学家克劳修斯提出的，用于描述一个系统混乱程度的度量，系统越混乱，熵越大

随着时代的发展，熵这一概念被香农引入到信息论中，即信息熵（Information Entropy），其将信息熵定义为信息中排除了冗余后的平均信息量

信息熵是信息量大小的度量，常用于描述离散随机变量的不确定性，不确定性越大，信息熵越大

设 $X$ 是来自于参数空间 $\mathcal{X}$ 的离散随机变量，其概率分布为：

$$P(X=x)=p(x)$$

则离散随机变量 $X$ 的信息熵定义为：

$$\begin{align*} H(X) &= \sum_{x\in X}p(x)\log \frac{1}{p(x)} \\ &= -\sum_{x\in X}p(x)\log p(x) \end{align*}$$

其中，上式中的对数 $\log$ 是以 $2$ 为底或以 $e$ 为底的对数，此时熵的单位分别称为 比特(bit)、纳特(nat)

需要注意的是，当信息熵的概率是由数据估计得到时，其被称为经验信息熵（Empirical Entropy）

取值范围

信息熵越大代表随机变量的不确定性越大，当变量可取值的个数一定时，其取每种值的概率分布越平均，熵值就越大

当取值种类为 $n$ 时，信息熵的取值范围为：

$$0\leq H(X) \leq \log n$$

当 $X$ 只有一个分类时，信息熵取最小值 $H(X)=0$；而当 $X$ 中 $n$ 个分类出现的概率相同，即 $p(x)=\frac{1}{n}$ 时，信息熵取最大值 $H(X)=\log n$

性质

香农给出了信息熵的三个性质：

1. 单调性：发生概率越高的事件，其携带的信息量越低
2. 非负性：信息熵可看作一种广度量，必有 $H(X)\geq 0$
3. 累加性：多随机事件同时发生存在的总不确定性的量度，可以表示为各事件不确定性量度的和

其中，对累加性的解释如下：

考虑到信息熵的定义涉及到了事件发生的概率，假设信息熵是事件发生概率的函数

对于两个相互独立的事件 $X = A$ ，$Y = B$ 来说，其同时发生的概率为：

$$P(X=A,Y=B)=P(X=A)\cdot P(X=B)$$

其同时发生的信息熵为：

$$\begin{align*} H(P(X=A,Y=B)) &= H(P(X=A)\cdot P(X=B))\\ &= H(P(X=A))+H(P(X=B)) \end{align*}$$

---

香农从数学上严格证明了满足上述条件的随机变量不确定性度量函数，具以下的唯一形式：

$$H(X)=-C\sum_{x}p(x)\log p(x)$$

其中，$C$ 为常数，当取 $C=1$ 时，即得到信息熵的公式

从信息熵的定义可以看出，信息熵是关于随机变量 $X$ 概率分布的函数，与 $X$ 的取值无关，因此，可将随机变量 $X$ 的信息熵记作 $H(p)$，即：

$$H(p)=-\sum_{x\in X}p(x)\log p(x)$$

二进制信息熵

当随机变量 $X$ 只取 $0$、$1$ 两个值时，$X$ 的分布为伯努利分布：

$$\left \{\begin{array}{rl} P(X=1) &=& p \\ P(X=0) &=& 1-p \end{array} \right.$$

此时，信息熵为二进制信息熵（Binary Information Entropy），也被称为伯努利分布下的信息熵：

$$\begin{align*} H_b(p) &= -p\log_2 p-(1-p)\log_2(1-p) \\ &= p\log_2\frac{1}{p}+(1-p)\log_2\frac{1}{1-p} \end{align*}$$

二进制信息熵 $H_b(p)$ 随概率 $p$ 变化的曲线下图所示

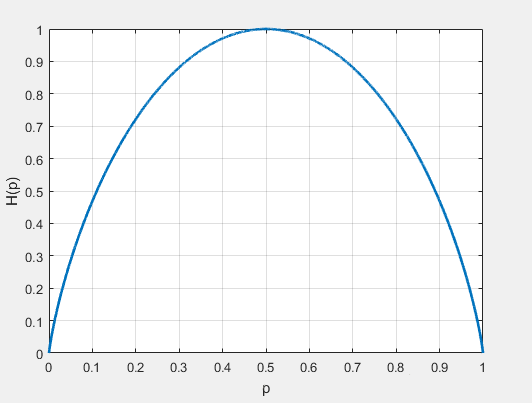
由图像可知：

• 当 $p=0$ 或 $p=1$ 时，$H_b(p)=0$，随机变量没有不确定性

• 当 $p=0.5$ 时，$H(p)=1$，随机变量不确定性最大

联合熵

对于二维离散随机变量 $(X,Y)$，其联合概率分布为：

$$P(X=x,Y=y)=p(x,y)$$

关于分量 $X$ 的边缘分布律为：

$$P(X=x)=p(x)$$

关于分量 $Y$ 的边缘分布律为：

$$P(Y=y)=p(y)$$

对于二维离散随机变量 $(X,Y)$，其联合熵（Joint Entropy）定义为：

$$H(X,Y)=-\sum_{x\in X}\sum_{y\in Y}p(x,y)\log p(x,y)$$

同样，当联合熵中的概率由数据估计得到时，其被称为经验联合熵（Empirical Joint Entropy）

此外，联合熵具有以下两条性质：

• $H(X,X)=H(X)$
• $H(X,Y)=H(Y,X)$

条件熵

条件熵（Conditional Entropy） $H(Y|X)$ 表示在已知随机变量 $X$ 的条件下，随机变量 $Y$ 的不确定性，其被定义为在给定条件 $X$ 的情况下 $Y$ 的条件概率分布的熵对 $X$ 的数学期望：

$$\begin{align*} H(Y|X) &= \sum_{x\in X}p(x)H(Y|X=x) \\ &= -\sum_{x\in X} p(x) \sum_{y\in Y} p(y|x)\log p(y|x) \\ &= -\sum_{x\in X}\sum_{y\in Y} p(x,y)\log p(y|x) \\ &= -\sum_{x\in X}\sum_{y\in Y} p(x,y)\log \frac{p(x,y)}{p(x)} \end{align*}$$

同样，当条件熵中的概率由数据估计得到时，其被称为经验条件熵（Empirical Conditional Entropy）

此外，条件熵具有以下两条性质：

• $H(X|Y)\neq H(Y|X)$
• $H(X|Y)+H(Y)=H(Y|X)+H(X)=H(X,Y)$

信息熵的链式法则

与概率的链式法则 $P(X,Y)=P(X|Y)P(Y)=P(Y|X)P(X)$ 相似，信息熵同样存在链式法则

由于信息熵是 $\log p$ 的期望，那么需要变相乘为相加，即有：

$$H(X,Y) = H(X|Y)+H(Y)= H(Y|X)+H(X)$$

【互信息】

互信息

互信息（Mutual Information）用于衡量随机变量 $X$、$Y$ 间的相互依赖程度，即在得知了 $X$ 的信息后，$Y$ 的信息的不确定性减少的程度

根据信息熵的链式法则，有：

$$H(X,Y)=H(Y|X)+H(X)=H(X|Y)+H(Y)$$

因此，有：

$$H(X)-H(X|Y)=H(Y)-H(Y|X)$$

这个差即为 $X$ 与 $Y$ 的互信息，记作 $I(X,Y)$，按照信息熵与联合熵的定义展开，有：

$$\begin{align*} I(X,Y) &= H(X)-H(X|Y) \\ &= H(X)+H(Y)-H(X,Y) \\ &= \sum_{x\in X}p(x) \log\frac{1}{p(x)} + \sum_{y\in Y} p(y)\log\frac{1}{p(y)}-\sum_{x\in X}\sum_{y\in Y}p(x,y)\log \frac{1}{p(x,y)} \\ &= \sum_{x\in X}\sum_{y\in Y} p(x,y)\log\frac{p(x,y)}{p(x)p(y)} \end{align*}$$

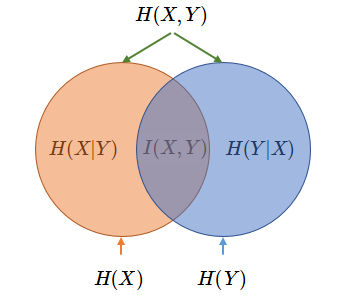
如下列 Venn 图所示，清晰地表示了信息熵 $P(X)$、$P(Y)$，联合熵 $P(X,Y)$，条件熵 $P(X|Y)$、$P(Y|X)$，互信息 $I(X,Y)$ 的关系

条件互信息

条件互信息（Conditional Mutual Information）用于表示给定第三个变量 $Z$ 的情况下，两个随机变量 $X$、$Y$ 间互信息的期望值

其被定义为：

$$\begin{align*} I(X,Y|Z) &= \sum_{z\in Z} p(z) \sum_{y\in Y} \sum_{x\in X} p(x,y|z) \log \frac{p(x,y|z)}{p(x,z)p(y,z)} \\ &= \sum_{z\in Z} \sum_{y\in Y} \sum_{x\in X} p(x,y,z) \log \frac{p(z)p(x,y,z)}{p(x,z)p(y,z)} \end{align*}$$

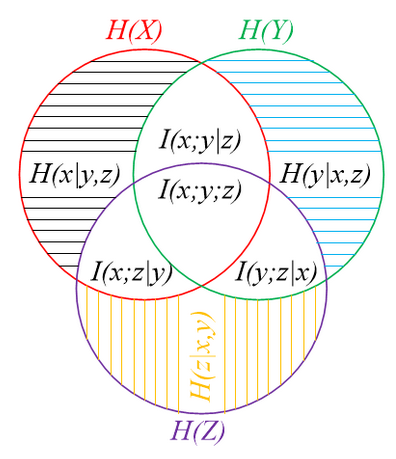
如下列 Venn 图所示，清晰地表示了信息熵 $P(X)$、$P(Y)$、$P(Z)$，条件熵 $P(X|Y,Z)$、$P(Y|X,Z)$、$P(Z|X,Y)$，互信息 $I(X,Y,Z)$，条件互信息 $I(X,Y|Z)$、$I(X,Z|Y)$、$I(Y,Z|X)$ 的关系