Reference
【判别分类模型】
假设分类模型为一判别模型,选用条件概率分布 $P(Y|X)$ 作为预测模型,$X\in\mathcal{X}\subseteq \mathbb{R}^n $ 为输入,$Y\in\mathcal{Y}\subseteq \mathbb{R}^n $ 为输出
该模型的含义为:对于给定的输入 $X$,以 $P(Y|X)$ 的概率输出 $Y$
【特征函数】
特征函数(Feature Function)用于描述输入 $x$ 与输出 $y$ 之间的某一事实,其定义为:
其是一个二值函数,用于将数据集数学化
举例来说,对于如下数据集:
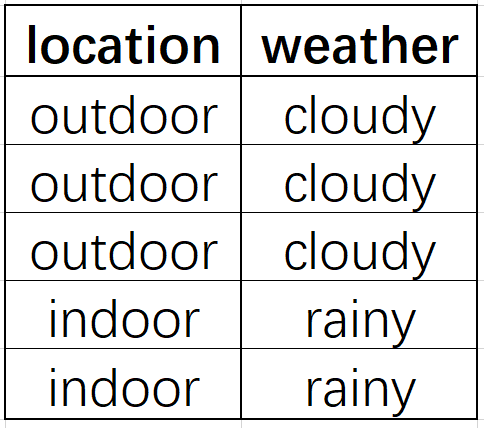
取第一列为 $x$,第二列为 $y$,可以为该数据集写出一些特征函数,例如:
如此,可以为每个 <特征,标签> 对都做一个如上的特征函数,以实现数据集数学化
【经验分布】
对于给定训练集,可将训练数据当做由随机变量 $(X,Y)$ 产生的,那么可根据训练数据来确定联合分布 $P(X,Y)$ 的经验分布 $\tilde{P}(X,Y)$ 与边缘分布 $P(X)$ 的经验分布 $\tilde{P}(X)$
记 $v(X=x,Y=y)$ 为训练集中样本 $(x,y)$ 的出现频数,$v(X=x)$ 为训练集中输入 $x$ 的出现频数,$n$ 为样本容量,则对于两个经验分布,有:
【约束条件】
对于来自参数空间 $\mathcal{X}$ 的离散随机变量 $X$,其概率分布为:
对于随机变量 $X$,其数学期望为 $E(X)=\sum\limits_{i=1}^nx_ip_i$,若 $Y=f(X)$,则关于 $X$ 的函数 $Y$ 的期望为:
按照期望的定义,对于任意的特征函数 $f(x,y)$,用 $E_{\tilde{p}}(f)$ 表示特征函数 $f(x,y)$ 关于经验分布 $\tilde{P}(X,Y)$ 的期望,有:
对于任意的特征函数 $f(x,y)$,用 $E_p(f)$ 表示特征函数 $f(x,y)$ 关于判别模型 $P(Y|X)$ 的期望,有:
对于判别模型 $P(Y|X)$,希望关于经验分布 $\tilde{P}(X,Y)$ 的期望 $E_{\tilde{p}}(f)$ 应该与从训练集中得到的关于经验分布 $\tilde{P}(X)$ 的期望 $E_p(f)$ 是一致的,为此,提出特征约束:
即:
上式即为最大熵模型中要满足的约束条件
需要注意的是,由于特征函数是对数据集实现数学化的,每个 <特征,标签> 对都会做一个特征函数,因此,若有 $m$ 个特征的话,就有 $m$ 个特征函数 $f_j(x,y)$ ,相应地,有 $m$ 个约束条件
满足所有约束条件的模型集合为:
【最大熵模型】
对于给定的训练集 $T$,目标是根据最大熵原理,选择一个最优的分类器
对于从训练集获得的特征函数和约束条件,将信息熵的概念应用到条件分布中,条件概率分布 $p(Y|X)$ 上的条件熵为:
此时,在约束条件的模型集合 $\mathcal{C}$ 中,条件熵最大的模型,即为最大熵模型
要注意的是,式中的对数取自然对数

