Reference:
【概述】
如果概率模型的变量都是观测变量(Observable Variable),又称显变量,即可以直接观测到的变量,那么当给定数据时,可以直接使用极大似然估计,或使用贝叶斯估计来估计模型的参数
但实际应用中,概率模型概率模型有时既含有观测变量,又含有潜在变量(Latent Variable),又称隐变量,即无法直接观测或测量的变量,此时就无法使用极大似然估计或贝叶斯估计来估价模型的参数
期望极大(Expectation Maximization,EM)算法,用于含有隐变量的概率模型参数的极大似然估计法,其是一种迭代算法,每次迭代由两步组成:
- E 步(Expectation-Step):通过观测变量和现有模型来估计参数,然后用这个估计的参数值来计算似然函数的期望值
- M 步(Maximization-Step):寻找似然函数最大化时对应的参数
【EM 算法的导出】
对数似然函数的极大化
对于给定的容量为 $n$ 的样本集 $D=\{(\mathbf{x}_1,y_1),(\mathbf{x}_2,y_2),…,(\mathbf{x}_n,y_n)\}$,每组样本中的输入 $\mathbf{x}_i$ 为观测变量,具有 $m$ 个特征值,即:$\mathbf{x}_i=(x_i^{(1)},x_i^{(2)},\cdots,x_i^{(m)})\in \mathbb{R}^m$,存在未观察到的隐变量集 $Z=(z_1,z_2,\cdots,z_n)$,即上述样本属于哪个分布是未知的,现有模型为 $f(\mathbf{x}_i;\boldsymbol{\theta})$,要求出样本的模型参数 $\boldsymbol{\theta}$ 使得 $f(\mathbf{x}_i;\boldsymbol{\theta})\simeq y_i$
设 $X=(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n)$ 为观测变量集,那么观测变量的似然函数为:
相应地,对数似然函数为:
可以通过极大似然估计来求解最优模型参数 $\boldsymbol{\theta}^*$,即:
但由于隐变量集 $Z$ 的存在,需要对每个样本的每个可能的 $z$ 求联合概率分布之和,于是对数似然函数 $\ln L(X;\boldsymbol{\theta})$ 有:
此时对模型参数 $\boldsymbol{\theta}$ 进行极大似然估计,就变为:
可以发现,对上式进行极大化的主要困难在于其中含有隐变量 $z$,并有包含和的对数,虽然可以使用梯度下降法来求解,但随着隐变量的数目的增加,求和项会以指数级上升,会给梯度计算带来麻烦
一个方法是构造一个容易优化的、关于对数似然函数的下界函数,通过不断优化这个下界,通过非梯度方法来迭代逼近最优参数 $\boldsymbol{\theta}^*$
对数似然函数的下界
引入一个未知的、关于隐变量 $Z$ 的某种概率分布 $Q(Z)$,且满足条件:
于是,对于对数似然函数,有:
由于 $\ln(\cdot)$ 的二阶导数小于 $0$,因此原函数为上凸函数,那么根据 Jensen 不等式,有:
注:这里用到的是 $\ln \sum\limits_z \lambda_z f_z \geq \sum\limits_z \lambda \ln f_z$,其中 $\lambda_z\geq 0,\sum\limits_z\lambda_z =1$
此时,即得到了对数似然函数 $\ln L(X;\boldsymbol{\theta})$ 的下界:
可以发现,$\sum\limits_{z}^Z Q(z) \ln \frac{p(\mathbf{x}_i,z;\boldsymbol{\theta})}{Q(z)}$ 是 $ \ln \frac{p(\mathbf{x}_i,z;\boldsymbol{\theta})}{Q(z)}$ 关于隐变量 $z$ 的数学期望,也就是说,确定对数似然函数 $\ln L(X;\boldsymbol{\theta})$ 下界 $J(Z,Q;\boldsymbol{\theta})$ 的过程,就是 EM 算法中的 E 步
对数似然函数下界的优化
在得到对数似然函数的下界 $J(Z,Q;\boldsymbol{\theta})$ 后,就可以通过不断优化这个下界来使得 $\ln L(X;\boldsymbol{\theta})$ 不断提高,那么,一个关键问题是,对于关于隐变量 $Z$ 的某种概率分布 $Q(Z)$ 应当如何选择?
假设参数 $\boldsymbol{\theta}$ 已经给定,那么 $J(Z,Q;\boldsymbol{\theta})$ 的值取决于 $Q(z)$ 和 $p(\mathbf{x}_i,z;\boldsymbol{\theta})$,就可以通过调整这两个概率使得下界 $J(Z,Q;\boldsymbol{\theta})$ 不断上升,从而逼近 $\ln L(X;\boldsymbol{\theta})$ 的真实值,当不等式变为等式时,说明调整后的下界 $J(Z,Q;\boldsymbol{\theta})$ 能够等价于对数似然函数 $\ln L(X;\boldsymbol{\theta})$
对于对数似然函数 $\ln L(X;\boldsymbol{\theta})$ 和下界 $J(Z,Q;\boldsymbol{\theta})$ :
当且仅当 $X=\mathbb{E}[X]$,即下式 $c$ 为常数时成立
由于 $Q(z)$ 是一个分布,满足 $\sum\limits_z^Z Q(z)=1$,因此有:
于是,对于 $Q(z)$,有:
也就是说,在固定了参数 $\boldsymbol{\theta}$ 后,使下界 $J(Z,Q;\boldsymbol{\theta})$ 提高的 $Q(z)$ 即后验概率
如果 $Q(z)=p(z|\mathbf{x}_i;\boldsymbol{\theta})$,那么 $J(Z,Q;\boldsymbol{\theta})$ 就是包含隐变量的对数似然函数的一个下界,只需要最大化这个下界,就是在极大化对数似然函数 $L(X;\boldsymbol{\theta})$,因此只需最大化下式即可
上式也即 EM 算法中的 M 步
【EM 算法流程】
输入:观测变量 $X=(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n)$,联合分布 $P(X,Z;\boldsymbol{\theta})$,条件分布 $P(Z|X;\boldsymbol{\theta})$
输出:模型参数 $\boldsymbol{\theta}=(\theta^{(0)},\theta^{(1)},\cdots,\theta^{(m)})$
算法流程:
Step1:随机初始化模型参数 $\boldsymbol{\theta}$ 的初值 $\boldsymbol{\theta}_0$
Step2:E 步,确定第 $k+1$ 次迭代的下界
1)记 $\boldsymbol{\theta}_k$ 为第 $k$ 次迭代参数 $\boldsymbol{\theta}$ 的估计值,在第 $k+1$ 次迭代时,计算联合分布的条件概率期望
2)在计算出 $Q_k(z)$ 后,确定第 $k+1$ 次迭代的下界
Step3:M 步,极大化第 $k+1$ 次迭代的下界,从而确定第 $k+1$ 次迭代的参数的估计值 $\boldsymbol{\theta}_{k+1}$
Step4:重复 Step2 与 Step 3,直到 $\boldsymbol{\theta}_{k+1}$ 收敛,即
其中,$\varepsilon$ 为一较小的正数
【EM 算法的直观解释】
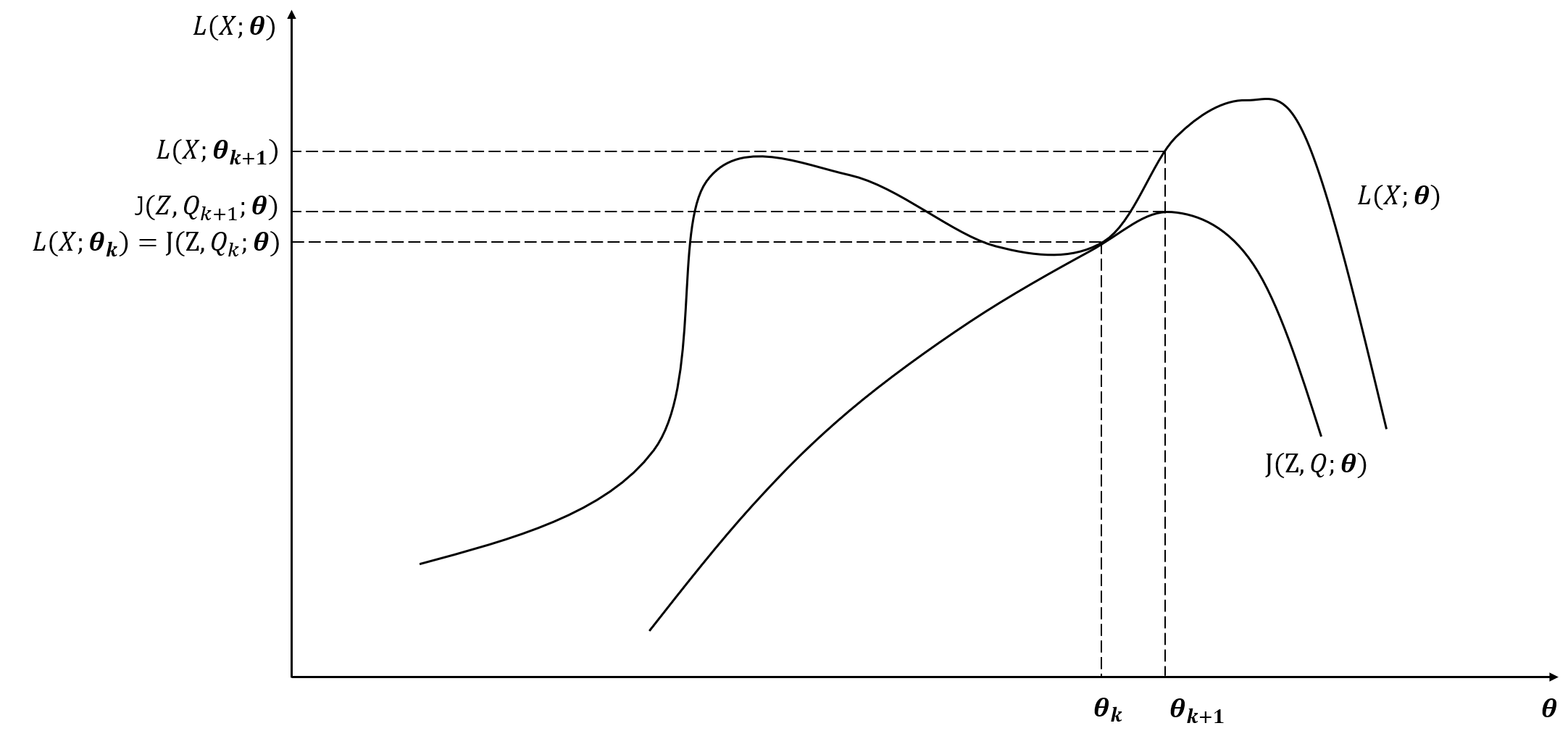
如下图所示,图中上方的曲线为对数似然函数 $L(X;\boldsymbol{\theta})$,下方的曲线为对数似然函数的下界 $J(Z,Q;\boldsymbol{\theta})$,两个函数在 $\boldsymbol{\theta}=\boldsymbol{\theta}_k$ 处相等,当 EM 算法找通过迭代找到下一个点 $\boldsymbol{\theta}_{k+1}$ 使 $J(Z,Q_{k+1};\boldsymbol{\theta})$ 极大化,由于 $L(X;\boldsymbol{\theta})\geq J(Z,Q;\boldsymbol{\theta})$,保证对数似然函数 $L(X;\boldsymbol{\theta})$ 也是增加的
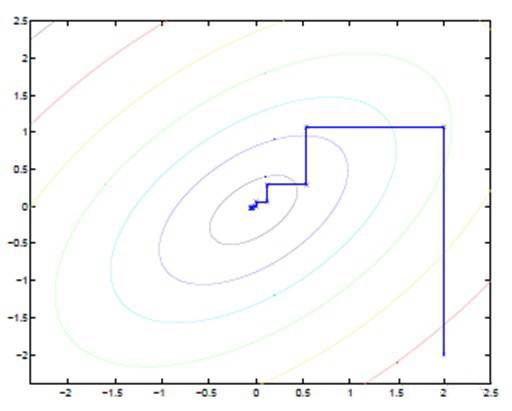
从另一种角度来看,EM 算法可视为坐标上升法,对于 E 步来说,相当于固定参数 $\boldsymbol{\theta}$ 优化 $Q(z)$,对于 M 步来说,相当于固定 $Q(z)$ 优化参数 $\boldsymbol{\theta}$,两者不断交替将极值推向最大
如下图所示,图中直线为迭代优化路径,由于每次只优化一个变量,可以看到其每走一步都是平行于坐标轴的