Alex_McAvoy

想要成为渔夫的猎手

最大熵模型学习的最优化算法

发表于 分类于 ， ，
本文字数： 8.9k 阅读时长 ≈ 8 分钟

Reference

【最大熵模型学习的最优化算法】

由于在最大熵模型中，对偶函数的极大化等价于最大熵模型的极大似然估计，那么最大熵模型的学习问题就转换为具体求解对偶函数 $\psi(\boldsymbol{\omega})$ 极大化或对数似然函数 $L_{\tilde{p}}(p_{\boldsymbol{\omega}})$ 极大化的问题，即：

虽然对偶函数 $\psi(\boldsymbol{\omega})=L_{\tilde{p}}(p_{\boldsymbol{\omega}})$ 是一个光滑的凸函数，但由于其规范化因子 $Z_{\boldsymbol\omega}(x)=\sum\limits_{y\in Y} \exp \Big[ \sum\limits_{j=1}^m \omega^{(j)}f_j(x,y) \Big]$ 中存在指数函数，几乎不可能有解析解，换言之，即使有解析解，但最终仍要求数值解

对于上述的问题，可以使用梯度下降法、牛顿法、拟牛顿法、迭代尺度法、改进的迭代尺度法等最优化方法，其中，改进的迭代尺度法（Improved Iterative Scaling，IIS）是专门用于最大熵模型学习的最优化算法

关于 IIS，详见：改进的迭代尺度法

【实例】

假设随机变量 $X$ 有 5 个取值 $\{A,B,C,D,E\}$，对应取值的概率分别为 $P(A)$、$P(B)$、$P(C)$、$P(D)$、$P(E)$，存在如下约束条件：

要求学习最大熵模型

为表示方便，令 $x_1$、$x_2$、$x_3$、$x_4$、$x_5$ 表示 $A$、$B$、$C$、$D$、$E$

于是，关于经验分布 $\tilde{P}(X)$ 的期望为：

关于模型 $P(Y|X)$ 与经验分布 $\tilde{P}(X)$ 的期望为：

此时，最大熵模型学习的最优化问题为：

引入拉格朗日乘子 $\omega^{(0)}$、$\omega^{(1)}$，并定义拉格朗日函数：

根据拉格朗日对偶性，通过求解对偶问题来得到原始问题的解，即求解：

首先求解 $L(p,\boldsymbol{\omega})$ 关于 $p$ 的极小化问题 $\psi(\boldsymbol{\omega})$ ，求偏导数 $\frac{\partial L(p,\boldsymbol{\omega})}{\partial p(x)}$，有：

令各项偏导数为 $0$，有：

故对偶函数为：

接着，解 $\psi(\boldsymbol{\omega})$ 的关于 $\boldsymbol{\omega}$ 的极大化问题

分别求 $\psi(\boldsymbol{\omega})$ 对 $\omega^{(0)}$、$\omega^{(1)}$ 的偏导，并令其为 $0$，联立后有：

故可得所要求的概率分布为：

【实现】

以 sklearn 中的鸢尾花数据集为例，选取其后两个特征来实现最大熵模型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from collections import defaultdict
import math
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import confusion_matrix,accuracy_score,classification_report,precision_score,recall_score,f1_score
from matplotlib.colors import ListedColormap

# 特征提取
def deal_data():
    iris = load_iris()  # sklearn的鸢尾花数据集
    # iris分为三类，前50行一类，51-100行一类，101-150行一类
    X = iris.data[:, [2, 3]] # 选用后两个特征作为样本特征
    y = iris.target  #取species列，类别
    return X,y

# 数据归一化
def standard_scaler(X_train,X_test):
    sc = StandardScaler() # 初始化一个sc对象去对数据集作变换
    scaler = sc.fit(X_train) # 归一化，存有计算出的均值和方差
    X_train_std = scaler.transform(X_train) # 利用 scaler 进行标准化
    X_test_std = scaler.transform(X_test) # 利用 scaler 进行标准化
    return X_train_std, X_test_std

# 特征重建
def features_rebuild(old_features):
    '''
    最大熵模型f(x,y)中的x是一个单独的特征，不是n维特征向量
    为此，要对每个维度加一个区分特征
    具体来说，将原来feature的(a0,a1,a2,...)变成(0_a0,1_a1,2_a2,...)的形式
    '''
    new_features = []
    for feature in old_features:
        new_feature = []
        for i, f in enumerate(feature):
            new_feature.append(str(i) + '_' + str(f))
        new_features.append(new_feature)
    return new_features

class MaxEnt(object):
    def init_params(self, X, Y):
        self.X_ = X
        self.Y_ = set()

        self.cal_Vxy(X, Y)

        self.N = len(X)                 # 数据集大小
        self.n = len(self.Vxy)          # 数据集中样本(x,y)的个数
        self.M = 10000.0                # 设置IIS算法中的学习速率M

        self.build_dict()
        self.cal_pxy()
        
    # 建立id:(x,y)字典和(x,y):id字典
    def build_dict(self):
        self.id2xy = {}
        self.xy2id = {}

        for i, (x, y) in enumerate(self.Vxy):
            self.id2xy[i] = (x, y)
            self.xy2id[(x, y)] = i
            
    # 计算样本(x,y)出现的频数v(X=x,Y=y)
    def cal_Vxy(self, X, Y):
        self.Vxy = defaultdict(int)

        for i in range(len(X)):
            x_, y = X[i], Y[i]
            self.Y_.add(y)
            
            for x in x_:
                self.Vxy[(x, y)] += 1

    # 计算联合分布p(X,Y)的经验分布p~(X,Y)
    def cal_pxy(self):
        self.pxy = defaultdict(float)
        for id in range(self.n):
            (x, y) = self.id2xy[id]
            self.pxy[id] = float(self.Vxy[(x, y)]) / float(self.N)

    # 计算规范化因子Zw(x)未加和前的单项Zw(x/yi)
    def cal_Zx(self, X, y):
        result = 0.0
        for x in X:
            if (x,y) in self.xy2id:
                id = self.xy2id[(x, y)]
                result += self.w[id]
        return (math.exp(result), y)

    # 计算条件概率p(Y|X)
    def cal_pyx(self, X):
        pyxs = [(self.cal_Zx(X, y)) for y in self.Y_]
        Zwx = sum([prob for prob, y in pyxs])
        return [(prob / Zwx, y) for prob, y in pyxs]

    # 计算未加和的前的特征函数f(x,y)关于模型p(Y|X)与经验分布p~(X)的期望值Ep(f)的单项Ep(f_i)
    def cal_Epfi(self):
        self.Epfi = [0.0 for i in range(self.n)]

        for i, X in enumerate(self.X_):
            pyxs = self.cal_pyx(X)

            for x in X:
                for pyx, y in pyxs:
                    if (x,y) in self.xy2id:
                        id = self.xy2id[(x, y)]

                        self.Epfi[id] += pyx * (1.0 / self.N)

    # IIS算法
    def fit(self, X, Y):
        self.init_params(X, Y) # 初始化参数
        max_iteration = 500  # 设置最大迭代次数
        
        # step1：初始化参数值wi=0
        self.w = [0.0 for i in range(self.n)]
        
        # step2：对每一参数进行操作
        for times in range(max_iteration):
            # step2.a：计算δi
            detas = []
            self.cal_Epfi()
            for i in range(self.n):
                # 指定的特征函数为指示函数，因此E~p(fi)等于p(X,y)
                deta = 1 / self.M * math.log(self.pxy[i] / self.Epfi[i])  
                detas.append(deta)

            # step2.b：更新wi
            self.w = [self.w[i] + detas[i] for i in range(self.n)]

    # 预测
    def predict(self, testset):
        results = []
        for test in testset:
            result = self.cal_pyx(test)
            results.append(max(result, key=lambda x: x[0])[1])
        return results
    
# 模型训练
def train_model(X_train_std, y_train):
    # 建立最大熵模型
    model = MaxEnt()
    # 训练
    model.fit(X_train_std, y_train)
    return model

# 模型评估
def estimate_model(y_pred, y_test, model):
    # 混淆矩阵，三分类情况下，大小为 3*3
    cm2 = confusion_matrix(y_test,y_pred) 
    # 准确率
    acc = accuracy_score(y_test,y_pred)
    # 正确分类的样本数
    acc_num = accuracy_score(y_test,y_pred,normalize=False)
    # macro 分类报告
    macro_class_report = classification_report(y_test, y_pred,target_names=["类0","类1","类2"])
    # 微精确率
    micro_p = precision_score(y_test,y_pred,average='micro') 
    # 微召回率
    micro_r = recall_score(y_test,y_pred,average='micro')
    # 微F1得分
    micro_f1 = f1_score(y_test,y_pred,average='micro') 
    
    indicators = {"cm2":cm2,"acc":acc,"acc_num":acc_num,"macro_class_report":macro_class_report,"micro_p":micro_p,"micro_r":micro_r,"micro_f1":micro_f1}
    return indicators

# 可视化
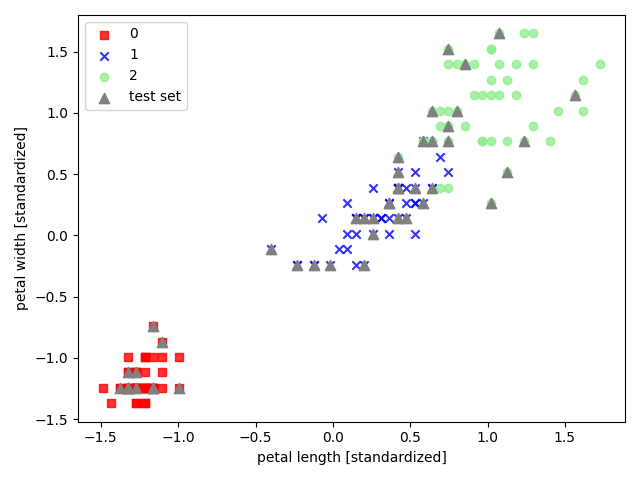
def visualization(X, y, classifier, test_id=None, resolution=0.02):
    for i in range(0,150):
        X[i][0] = X[i][0].replace("0_","")
        X[i][1] = X[i][1].replace("1_","")
    X = X.astype(float)

    # 创建 color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])
    
    # 全数据集，不同类别样本点的特征作为坐标(x,y)，用不同颜色画散点图
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl) 
        
    # 高亮测试集
    if test_id:
        X_test, y_test = X[test_id, :], y[test_id]
        # c设置颜色，测试集不同类别的实例点画图不区别颜色
        plt.scatter(x=X_test[:, 0], y=X_test[:, 1], alpha=1.0, c='gray', marker='^', linewidths=1, s=55, label='test set')
        
    plt.xlabel('petal length [standardized]')
    plt.ylabel('petal width [standardized]')
    plt.legend(loc='upper left')
    plt.tight_layout()
    plt.show()
    
if __name__ == '__main__':
    # 特征提取
    X, y = deal_data()
    
    # 简单交叉验证
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

    # 数据标准化
    X_train_std, X_test_std = standard_scaler(X_train, X_test)

    # 特征重建
    X_train_std = features_rebuild(X_train_std)
    X_test_std = features_rebuild(X_test_std)
    
    # 模型训练
    model = train_model(X_train_std, y_train)
    
    # 预测结果
    y_pred = model.predict(X_test_std)
    print("y test:", y_test) # 测试集y值
    print("y pred:", y_pred) # 预测y值
    
    # 模型评估
    indicators = estimate_model(y_pred, y_test, model)
    cm2 = indicators["cm2"] 
    print("混淆矩阵：\n", cm2) 
    acc =  indicators["acc"]
    print("准确率：", acc)
    acc_num =  indicators["acc_num"]
    print("正确分类的样本数：", acc_num)
    macro_class_report = indicators["macro_class_report"]
    print("macro 分类报告：\n", macro_class_report)
    micro_p = indicators["micro_p"]
    print("微精确率：", micro_p)
    micro_r = indicators["micro_r"]
    print("微召回率：", micro_r)
    micro_f1 = indicators["micro_f1"]
    print("微F1得分：", micro_f1)
    
    # 可视化
    X_combined_std = np.vstack((X_train_std, X_test_std))    
    y_combined = np.hstack((y_train, y_test))
    # classifier为分类器，test_id为测试集序号
    visualization(X_combined_std, y_combined, classifier=model, test_id=range(105, 150))
感谢您对我的支持，让我继续努力分享有用的技术与知识点！