Reference
【概述】
评价指标可以说明模型的性能,辨别模型的结果,在建立一个模型后,计算指标,从指标获取反馈,再继续改进模型,直到达到理想的效果,因此,在预测之前检查模型的评估指标至关重要,不应在建立一个模型后,就直接将模型应用到看不见的数据上
对于分类问题来说,其根据所分类别的个数,可分为二分类问题、多分类问题
在二分类问题中,使用的评价指标有:误差率(Error Rate)、准确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1 分数(F1 score)、$F_\beta$ 分数($F_\beta$ score)、PR 曲线、ROC 曲线、AUC、代价敏感错误率(Cost-sensitive Error Rate)、代价曲线(Cost Curve)等
在多分类问题中,使用的评价指标有: 宏精确率(macro-P)、宏召回率(macro-R)、宏 F1(macro-F1) 、微精确率(micro-P)、微召回率(micro-R)、微F1(micro-F1)等
本文将详细介绍 ROC 曲线、AUC
【ROC 曲线】
在根据预测结果对样例进行排序时,排序本身的质量好坏,体现了综合考虑模型在不同任务下的泛化性能的好坏,ROC 正是从这个角度出发来研究模型的泛化性能
ROC 全称是受试者工作特征(Receiver Operating Characteristic),与 P-R 曲线相似,根据模型的预测结果对样例进行排序,按顺序逐个将样本作为正类进行预测,每次计算真正类率(True Positive Rate,TPR)、假正类率(False Positive Rate,FPR),并将他们作为纵轴、横轴来绘制曲线
如下图,将 TPR 作为纵轴,FPR 作为横轴,即可绘制出 ROC 曲线
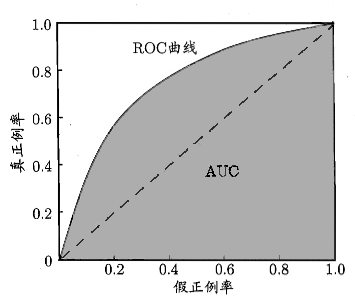
对于样本数据,使用分类器对其进行分类,分类器会给出每个数据为正例的概率,由此可以来设定一个阈值,当某个样本数据被判断为正例的概率大于这个阈值时,即认为该样本为正例,小于则为负例,然后通过计算就可以得到一个 (TPR , FPR) 坐标对,即图像上的一个点,之后通过不断调整这个阈值,就得到若干个点,从而画出一条近似 ROC 曲线,再用线性插值补全间断处
当阈值越大时,就会使越多的样本被分为负例,会使得正例样本被分为负例,从而导致 TPR 下降,同时,负例样本更不会被分为正例,FPR 也会下降,但是影响要比 TPR 小,因此随着阈值的增大,$\frac{FPR}{TPR}$ 呈上升趋势
当阈值越小时,就会使越多的样本被分为正例,会使得负例样本被分为正例,从而导致 TPR 上升,同时,正例样本会被分为正例,FPR 也会上升,但影响要比 TPR 大,因此,随着阈值的减小,$\frac{FPR}{TPR}$ 呈下降趋势
举例来说,在医疗诊断中,判断有病的样本,那么将有病的样本找出是主要任务,也就是要求真正类率越高 TPR 越好,而将没病的样本误诊为有病的,也就是要求假正类率 FPR 越低越好,不难发现,TPR 与 FPR 这两个指标是相互制约的
一般来说,分类器会对一批数据的每个样本给出一个是正例的概率,如下图所示,共 $20$ 个样本,class 为实际标签,score 为分类器判断样本为正例的概率
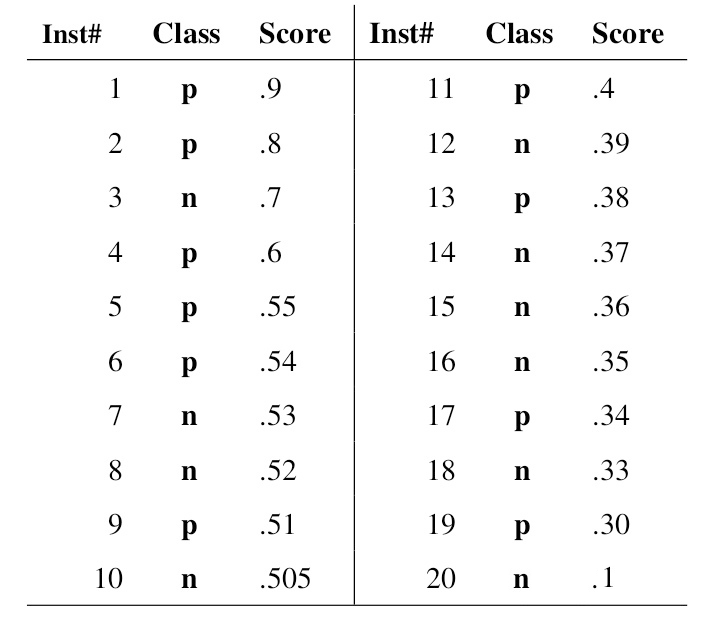
对给出的 score 进行排序,然后依次使用 score 作为阈值,这样就得到了 $20$ 组 (TPR , FPR) 坐标对,绘制出的 ROC 曲线如下
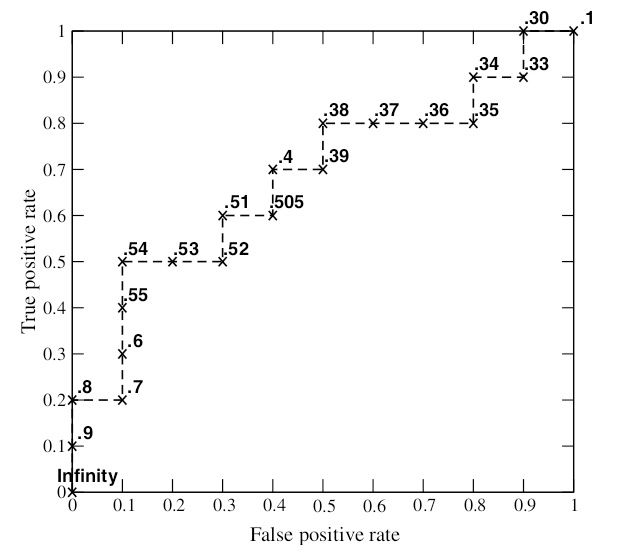
【AUC】
与 P-R 曲线类似,在进行模型比较时,如果一个模型的 ROC 曲线被另一个模型的 ROC 曲线完全包住,则可断言后者的性能优于前者,若两模型的 ROC 曲线发生交叉,则难以断言两者的优劣
如果一定要对两交叉的 ROC 曲线对应的模型进行比较,则对两 ROC 曲线下的面积进行比较
AUC(Area Under ROC Curve)被定义为 ROC 曲线下的面积,显然这个面积小于 $1$,又因为 ROC 曲线一般都处于 TPR = FPR 这条直线的上方,因此 AUC 一般都在 $0.5$ 到 $1$ 之间

假设分类器的输出是样本属于正类的置信度 score,那么 AUC 的物理意义就是:任取一对正例、负例样本,正样本的 score 大于负样本的 score 的概率
从图像来看,横轴是假正类率 FPR,即所有实际为负类但被判为正类的概率;纵轴是真正类率 TPR,即所有实际为正类也被判正类的概率
当 TPR = FPR 时,即上图中的虚线,此时无论真实类别为正类还是为负类的样本,分类器将其预测为正类的概率相等,即分类器对于样本毫无区分能力,与掷骰子没有任何区别
而分类器希望达到的效果是:对于真实类别为正类,分类器预测为正类的概率,要大于真实类别为负类,分类器预测为正类的概率,即:TPR > FPR,也就是上图中的实线曲线
在最理想的情况下,没有真实类别为正类,但被错分为负类的样本,即 TPR = 1;也没有真实类别为负类,但被错分为正类的样本,即 FPR = 0,此时,AUC = 1
由此,可以总结出从 AUC 判断分类器优劣的标准:
AUC = 1:完美分类器,最理想的情况,实际不存在0.5 < AUC < 1:优于随机猜测,妥善设定阈值的情况下,模型具备预测价值AUC = 0.5:与随机猜测一样,模型不具备预测价值AUC < 0.5:不如随机猜测,但只要总是反预测的话,就优于随机猜测
形式化来看,AUC 考虑的是样本预测的排序质量,因此其与排序误差有着紧密的联系
对于样本容量为 $n$ 的测试集 $T$ 来说,假设有 $n^+$ 个正例和 $n^-$ 个负例,令 $T^+$ 为正类集合,$T^-$ 为负类集合,那么 ROC 曲线上方的面积即排序损失 $\ell_{rank}$,其被定义为:
即考虑总共 $n^+n^-$ 个正例、负例对,若正例预测值要小于负例,那么就记录 $1$ 个罚分,对于正例预测值与负例相等的情况,由于数量的原因,需要乘以 $\frac{1}{2}$,即记录 $0.5$ 个罚分,最后再使用 $ \frac{1}{n^+n^-}$ 进行归一化
若一个正例在 ROC 曲线上对应标记点的坐标为 $(x,y)$,那么 $x$ 代表 score 比其高的负例数,也就是说,在 ROC 曲线中,从 $(0,0)$ 开始,每遇到一个正例,向上走一步,每遇到一个负例,向右走一步
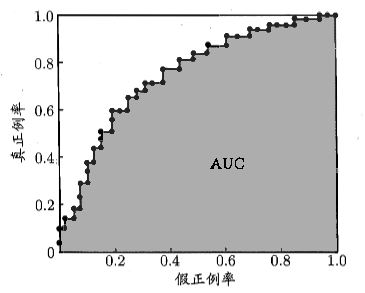
在实际应用中,无法产生类似光滑 ROC 曲线,只能绘制出如下图的近似 ROC 曲线

根据 AUC 的定义,AUC 可通过对 ROC 曲线下各部分的面积求和取得,假设 ROC 的曲线是由坐标 $\{(x_1,y_1),(x_2,y_2),…,(x_n,y_n)\}$ 的点按序连接而形成的,则 AUC 可估算为:
【Iso-performance 直线】
ROC 曲线一个优点是,其与测试样本的类别分布的误分类代价无关,即无论测试样本的正类负类的比例如何变化,都不会影响到分类器的 ROC 曲线
假设测试样本中正类所占比例为 $p(+)$,负类所占比例为 $p(-)$,记误分类代价 $C(-|+)$ 为实际为正类但被预测为负类的代价,$C(+|-)$ 为实际为负类但被预测为正类的代价
那么可以得到一个指定的 (类别分布,误分类代价),这被称为一个运行条件(Operating Condition),即:
以 $S$ 为斜率,在 ROC 空间中通过平移,可以得到许多条直线,这些直线被称为 Iso-performance 直线,每条直线上的所有点对应的分类器都具有相同的期望代价,且越靠近左上角的 Iso-performance 直线,对应的分类器的性能越好

