分类问题的评价指标（一）

【概述】

评价指标可以说明模型的性能，辨别模型的结果，在建立一个模型后，计算指标，从指标获取反馈，再继续改进模型，直到达到理想的效果，因此，在预测之前检查模型的评估指标至关重要，不应在建立一个模型后，就直接将模型应用到看不见的数据上

对于分类问题来说，其根据所分类别的个数，可分为二分类问题、多分类问题

在二分类问题中，使用的评价指标有：误差率（Error Rate）、准确率（Accuracy）、精确率（Precision）、召回率（Recall）、F1 分数（F1 score）、$F_\beta$ 分数（$F_\beta$ score）、PR 曲线、ROC 曲线、AUC、代价敏感错误率（Cost-sensitive Error Rate）、代价曲线（Cost Curve）等

在多分类问题中，使用的评价指标有： 宏精确率（macro-P）、宏召回率（macro-R）、宏 F1（macro-F1） 、微精确率（micro-P）、微召回率（micro-R）、微F1（micro-F1）等

本文将详细介绍误差率（Error Rate）、准确率（Accuracy）、精确率（Precision）、召回率（Recall）、F1 分数（F1 score）、$F_\beta$ 分数（$F_\beta$ score）、PR 曲线

【误差率与准确率】

错误率与准确率是分类问题中最常用的两种性能度量，既适用于二分类问题，又适用于多分类问题

误差率（Error Rate）是分类错误的样本数占据总样本的比例，即如果在 $m$ 个样本中有 $a$ 个样本分类错误，则误差率为：

$$E=\frac{a}{m}$$

相应地，将分类正确的样本数占据总样本的比例称为准确率（Accuracy）

---

对于给定测试集 $T=\{(\mathbf{x_1},y_1),(\mathbf{x_2},y_2),…,(\mathbf{x_N},y_N)\}$，学习到的模型为 $Y=f(X;\boldsymbol{\theta})$

误差率（Error Rate）为：

$$E_T(f)=\frac{1}{N}\sum_{i=1}^{N} \mathbb{I}(y_i\neq f(\mathbf{x_i};\boldsymbol{\theta}))$$

准确率（Accuracy）为：

$$ACC_T(f)=\frac{1}{N}\sum_{i=1}^{N} \mathbb{I}(y_i= f(\mathbf{x_i};\boldsymbol{\theta}))$$

其中，$\mathbb{I}(\cdot)$ 为指示函数，即满足函数中的条件时，值为 $1$，不满足时为 $0$

显然有：

$$E_T(f)=1-ACC_T(f)$$

虽然准确率能够判断总的预测正确率，但是在样本不均衡的情况下（例如有 $90$ 个样本 $10$ 个负样本），准确率高并没有任何意义，此时准确率就会失效，无法作为一个较好的指标来衡量结果

【混淆矩阵】

对于二分类问题，通常以关注的类为正类，其他类为负类，这样将样例根据其真实类别与预测类别的组合划分为真正类（True Positive，TP）、假正类（False Positive，FP）、真负类（True Negative，TN）、假负类（False Negative，FN）四种情形，显然有：

$$TP+FP+TN+FN=样例总数$$

相应地，分类结果的混淆矩阵（Confusion Matrix）如下

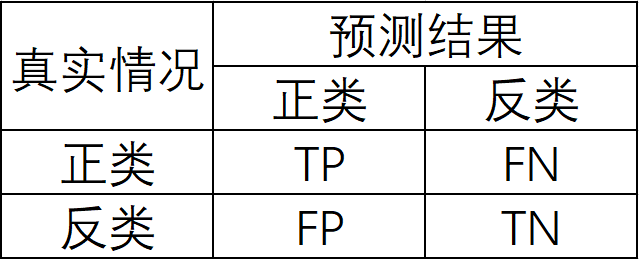
由此，可定义出如下四个概念：

真正类率（True Positive Rate，TPR）：在所有实际为正类的样本中，被正确预测为正类的比例

$$TPR=\frac{TP}{TP+FN}$$

真负类率（True Negative Rate，TNR）：在所有实际为负类的样本中，被正确预测为负类的比例

$$FNR = \frac{TN}{FP+TN}$$

假正类率（False Positive Rate，FPR）：在所有实际为负类的样本中，被错误预测为正类的比例

$$FPR=\frac{FP}{FP+TN}$$

假负类率（False Negative Rate，FNR）：在所有实际为正类的样本中，被错误预测为负类的比例

$$FNR = \frac{FN}{TP+FN}$$

【精确率与召回率】

精确率（Precision）是针对预测结果而言的，表示预测为正类中有多少是真正的正类，也就是说预测的有多少预测对了，其定义为：

$$P=\frac{TP}{TP+FP}$$

召回率（Recall）是针对原来样本而言的，表示样本中的正类有多少被正确预测了，也就是说样本里的正类有多少被找出来了，其定义为：

$$R=\frac{TP}{TP+FN}$$

可以发现，精确率与召回率是一对矛盾的度量，一般来说，当精确率高时，召回率偏低；当召回率高时，精确率偏低

【P-R 曲线】

在大多数情形下，根据预测结果对样例进行排序，排在前面的是模型认为最可能是正类的样本，排在最后的是模型认为最不可能是正类的样本

按上述的顺序，逐个将样本作为正类进行预测，每次可以计算出当前的精确率和召回率，之后，以精确率为纵轴，召回率为横轴绘制二维函数图，即可得到精确率-召回率曲线（Precision Recall Curve），即 P-R 曲线

举例来说，对于逻辑回归问题，其输出值处于 $0$ 到 $1$ 之间，如果想判断一个西瓜的好坏，就必须要定一个阈值，例如大于 $0.5$ 时为好西瓜，小于 $0.5$ 时为坏西瓜，此时即可得到相应的精确率与召回率，但这个阈值是我们随意定义的，不能确定其是否真的符合我们的要求，因此为了寻找一个合适的阈值，就要遍历 $0$ 到 $1$ 之间的所有阈值，每个阈值都对应一组精确率和召回率，进而即可得到一组 P-R 曲线

P-R 曲线直观地显示出了模型在样本总体上的精确率、召回率，在进行比较时，如果一个模型的 P-R 曲线被另一个模型的 P-R 曲线完全包住，则可断言后者的性能优于前者；如果两个模型的 P-R 曲线发生交叉，则一般难以断言两者优劣，只能在具体的精确率、召回率下进行比较

如下图所示，曲线 A 完全包住曲线 C，可以断言模型 A 要优于模型 C；而曲线 A 与曲线 B 发生了交叉，两者难以比较

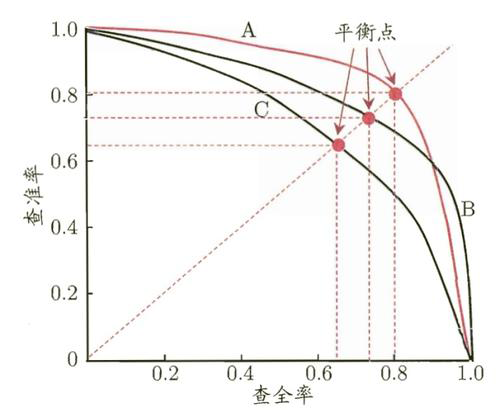
但有时，仍希望将两个发生交叉的曲线所分别对应的模型进行比较，此时一般比较两者曲线下面积的大小，其在一定程度上表征了模型在精确率和召回率上取得了双高的比例

但由于面积并不好进行估算，为此设计了平衡点（Break-Even Point，BEP），来综合考虑精确率与召回率，其是 精确率 = 召回率 时的取值

在上图中，基于 BEP 的比较，可以断定，模型 A 优于模型 B、模型 C，模型 B 优于模型 C

【F1 分数】

BEP 是 精确率 = 召回率 时的取值，过于简单粗暴了一些，于是定义了一个新的指标：F1分数（F1-Score），其同时考虑精确率和召回率，让两者同时达到最高，取得平衡

F1 分数被定义为精确率和召回率的调和均值（Harmonic Mean）：

$$\frac{2}{F_1}=\frac{1}{P}+\frac{1}{R}$$

即：

$$\begin{align*} F_1 &= \frac{2 \cdot P \cdot R}{P+R}\\ &= \frac{2 \cdot TP}{2\cdot TP+FP+FN} \notag \\ \end{align*}$$

【$F_\beta$ 分数】

在实际应用中，对于不同的情景对精确率和召回率的要求不同，例如：在推荐系统中，更希望推荐内容是用户感兴趣的，此时精确率更为重要；在逃犯信息检索系统中，更希望能够少漏掉逃犯，此时召回率更为重要

为此，有了 F1 分数的一般形式 $F_{\beta}$ 分数，其能表达出对精确率、召回率的不同偏好，其被定义为精确率、召回率的加权调和均值（Weighted Harmonic Mean）：

$$\frac{1}{F_\beta}=\frac{1}{1+\beta^2}(\frac{1}{P}+\frac{\beta^2}{R}),\quad \beta>0$$

即：

$$F_\beta=\frac{(1+\beta^2) \cdot P \cdot R}{(\beta^2 \cdot P)+R},\quad \beta>0$$

其中，$\beta$ 度量了召回率对精确率的相对重要性

• 当 $\beta=1$ 时：退化为 F1 分数
• 当 $\beta<1$ 时：精确率有更大的影响
• 当 $\beta>1$ 时：召回率有更大的影响